Для создания модели системы необходимо сначала дать ее вербально-информационное описание, (слово вербальный означает «словесный» от лат. “verbalis”)

2. Для создания модели системы необходимо сначала дать ее вербально-информационное описание, (слово вербальный означает «словесный» от лат. “verbalis”)

Его составные описывают:

1)    внешнюю среду;

2)    связи системы с внешней средой;

3)    элементарный состав системы, ее части, которые могут рассматриваться как системы меньшего размера;

4)    описание связей между элементами системы и ПС или главные связи между элементами и ПС, если нельзя дать все связи;

5)    действие системы..

Такое описание можно считать начальной моделью системы, базой для создания других более специализированных моделей высшего уровня.

Некоторые части описания могут быть неполными. Иногда (если система сложная) моделирование оканчивается вербальным описанием. Если вербальная модель удачная, то она позволяет принимать эффективные решения, решать разные проблемы, разрабатывать способы управления системой.

 

3.Использование численных математических методов моделирования позволило создать модели мировой экономики. Так как ресурсы Земли ограничены, то интересной является проблема исследования возможных последствий экономического роста. Эта проблема тесно связана с экономическими факторами.

Американский ученый Дж. Форрестер предложил модель мировой динамики. Интегральная выходная величина модели – индекс материального роста жизни

M = C/P * N(1-a),

где С – суммарный капитал, (инвестиции в промышленность),

Р – численность населения;

N – наличие природных ресурсов;

a – индекс сельскохозяйственного капитала.

Все переменные здесь есть усредненными величинами по всему миру.

Взаимосвязь переменных описывалась системой из 20 нелинейных уравнений. Использовалось имитационное моделирование.

Результаты оказались неутешительными:

1) если мир не изменится, то качество жизни будет снижаться после max в 70-е годы.

2) увеличение капиталовложений в промышленность вызовет загрязнение окружающей среды.

3) некоторое стабильное состояние можно достичь, если уменьшить капиталовложения в промышленность, рождаемость и пользование природных ресурсов.

Исследования мировой динамики продолжил Д.Медоуз. Его модель характеризуется величинами:

1 – наличие ресурсов;

2 – объемом производства продуктов питания на душу населения;

3 – численность населения;

4 – объемом промышленной продукции на душу населения;

5 – уровнем загрязнения окружающей среды;

6 – общим темпом смертности;

7 – общим темпом рождаемости;

8 – объемом производства услуг на душу населения(за год).

Процесс построения модели включал 4 этапа.

1) определение связей между 8 характеристиками системы;

2) составление зависимостей между характеристиками;

3) компьютерный расчет общего поведения этих зависимостей во времени;

4) исследования влияния на глобальную систему различных стратегий развития.

Согласно этой модели производство продуктов питания и численностъ населения растут, пока их не затормозит быстрое снижение ресурсных запасов. Загрязнения природной среды и численность населения растут после пика промышленного развития настолько, что вызовут экономическую, демографическую и экологическую катастрофу.

Чтобы убрать крах мировой системы, в модель последовательно вводили 4 стратегии технического прогресса:

1) широкое использование ядерной энергетики, чтобы удвоить ресурсы, переработка отходов. 2) контроль загрязнения природной среды. 3) увеличение продуктивности земли в 2 раза. 4) контроль за рождаемостью. Однако моделирование показало, что даже при одновременном использовании всех 4 стратегий уменьшается производство продуктов питания и промышленной продукции на душу населения.

Тогда разработали стабилизирующую стратегию, которая включала следующие предложения:

1) идеальный контроль за рождаемостью (2-е детей в семье);

2) увеличение амортизационных отчислений;

3) переработка вторичных ресурсов, контроль над состоянием окружающей среды, увеличение сроков службы всех видов капитала, обновление эрозийных земель.

Эти мероприятия должны были быть введены ещё в 1975г., иначе выход мира до стабильного состояния будет невозможен.

Эти выводы вызвали оживленную дискуссию. К критическим мнениям относились: сильная агрегированность модели, игнорирование больших различий между регионами Земли.

Другие модели были вообще необъяснимыми.

В научных кругах модели мировой динамики вызвали "футурошок" т.е.

ЛЕКЦИЯ 4

Тема :Моделирование экономических функций

 План

1 Функция издержек

2 Функция спроса

3 Функция предложения

4 Функция полезности

1.                Анализ издержек содержит изучение влияния издержек производства на объем производства и другие ТЭ показатели.

Чаще всего рассматривается функция вида:

Z=F(x)+Σbivi, i=1,n,

где Z - суммарные издержки;

x - количество продукции;

vi - другие условия, отражают различную структуру ОПФ, разные условия производства, разную организацию труда в различных отраслях.

Поделим обе части на X

 ,

где - удельные издержки.

Отвлечемся от влияния факторов , что, возможно при изучении издержек в общегосударственных масштабах. Тогда

Z=f(x),

,

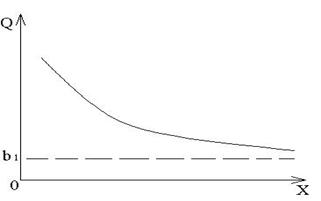
Линейная функция издержек имеет вид:

Z=f(x)=b0+bix.

Функция удельных издержек будет убывающей. Параметры можно интерпретировать с помощью предельных величин

,i=1,n;

фактор ∆Vi при неизменных уровне выпуска продукции увеличивает издержки на ∆Z,

∆Z=bi∆Vi.

Если ∆Vi=1, то ∆Z=bi..

Когда Vi выражает какой- то процесс или такое изменение организационной структуры, при котором издержки должны снизится, то bi должно иметь отрицательный знак.

2. Функция спроса выражает зависимость спроса от экономических (доходы, цены) и внешнеэкономических (потребительские привычки) факторов. Функции спроса могут быть как макроэкономическими, если охватывают всю сферу потребления и микроэкономическими описывающими спрос индивидуальных потребителей.

D (p) - функция спроса или просто спрос (по англ. “demand” - спрос)(количество товара покупаемого на данном рынке за единицу времени по цен Р за единицу). Фундаментальное свойство функции спроса выражает следующая аксиома: функция спроса является убывающей, при увеличении цены величина спроса на товар уменьшается к 0, при уменьшении цены товара величина спроса увеличивается.

Рассмотрим следующие функции спроса:

  

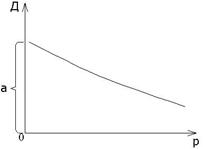
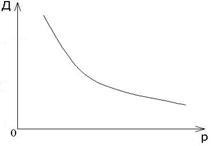
a) б) в)

а) линейно убывающая

D (p) =а-bp, .

б) обратная

D (p)=1/p, р>0,

 

в) логарифмическая

D (p)=ln (1+p)/p,p>0.

При изменении условий на рынке или вне его функция спроса может изменится, тогда говорят об изменении спроса. Изменение спроса надо отличать от изменения величины спроса при передвижении по графику данной функции спроса. Например, при повышении цен на бензин вполне может повысится спрос на велосипеды. Это означает, что вся кривая спроса передвинется вправо.

Рассмотрим математические характеристики кривой спроса и их экономические иллюстрации. Производная функции спроса по цене

,

показывает насколько изменится величина спроса при изменении цены товара на 1 ед. Т.к. функция спроса убывающая, то эластичность спроса по цене показывает на сколько % изменится величина спроса при изменении цены товара на 1 %.

Обозначается эластичность

.

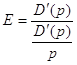3. S(p) - функция предложения или предложение (от англ.“supply”- предложение)(количество товара поставляемого на данный рынок за единицу времени при цене р за ед. товара). Функция предложения является возрастающей. Аксиома предложения: при увеличении цены величина предложения товара неограниченно увеличивается, при уменьшении цены величина предложения уменьшается, приближаясь к 0.

Различают функции предложения

  

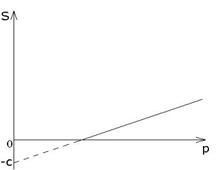
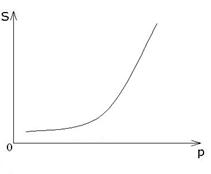
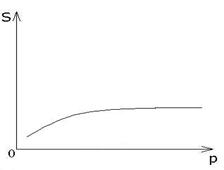
а)б) в)

а) линейно возрастающая

S (p) = - C + dp,,

б) степенная

,

в) логарифмическая

.

При изменении условий на рынке или вне него функция предложения может изменится, тогда говорят об изменении предложения. При открытии поблизости месторождения алмазов может увеличится предложение необработанных алмазов а возможно через некоторое время - ювелирных украшений.

Рассмотрим математические характеристики кривой предложения и их экономические иллюстрации.

Производная функции по цене

,

 показывает насколько изменится величина предложения при изменении цены товара на 1 ед. Т.к. функция предложения возрастающая, то

Эластичность предложения по цене показывает на сколько % изменится предложение при изменении цены товара на 1 %. Обозначается эластичность

;

Рассмотрим :

a)  

  ;

б)  ;

 ;

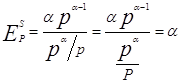в)  ;

.

4 Система предпочтений индивида указывает, какой из двух наборов предпочтительнее для него. Во многих случаях, однако, весьма желательно и удобно оценивать привлекательность набора товаров количественно , приписать каждому набору X из пространства товаров С какое-то число и(Х). Получается функция и: СR. Главное требование к такой функции, чтобы она отражала отношение (слабого) предпочтения на С, т.е. удовлетворяла условиям :

и(Х) < u{Y), если и только если X < Y

и(Х) = u(Y), если и только если X~Y, значит и

и(Х) < и(У), если и только если Х< Y.

Такая функция называется функцией полезности. Видно, что функция полезности постоянна на каждом классе равноценности, так что ее и вполне правильно представлять себе как функцию, "пересчитывающую" классы равноценности в сторону все большего предпочтения наборов товаров.

Работать с функцией полезности гораздо удобнее, чем с системой. Однако математики выяснили, что если на систему не накладывать никаких ограничений, кроме уже рас­смотренных ранее, а именно, транзитивность, совершенность и рефлексивность, то функции полезности может и не существовать. Тем не менее при некоторых естественных условиях, наложенных на систему функция полезности существует.

Теперь можно сформулировать условия, при которых существует функция полезности.

Теорема Если система предпочтений непрерыв­на, то существует непрерывная функция полезности.

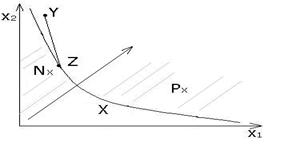 Рис.4.1

Надо отметить, что функцияполезности, если она существует, не определяется единственным образом ( рис.4.1).

 Основные свойства функции полезности вытекают из ее связи и подчиненности системе предпочтений. Функция полезности неубывающая и дифференцируема.

Состояние рынка, при котором спрос равен предложению называется равновесным, а цена, при которой достигается равенство спроса и предложения -называется равновесной ценой

Теоремa Пусть функции спроса и предложения непрерывны и, D(р₀) > S(p₀) при некоторой цене р₀; тогда существует состояние равновесия.

ЛЕКЦИЯ 5

 Тема: Типы производственных функций и их свойства

 План

1. Типы производственных функций

2. Предельный анализ факторов и однородность производственных функций

3. Эластичность производственных функций

4. Замещение факторов в производственных функциях

5. Производственная функция Кобба-Дугласа

1. Производственные функции можно разделить по количеству используемых переменных, по виду функций и по их свойствам.

Под производственной функцией понимают уравнение, связывающее выпуск продукции и затраты. Производственные функции по количеству переменных различают:

-     однофакторные:  или ;

-     двухфакторные: ;

-     многофакторные.

По аналитическому виду:

А) линейные производственные функции

.

Здесь параметры  и  выражают производительность факторов  и , то есть показывают абсолютный прирост производства, когда один фактор остается неизменным, а другой возрастает на единицу. Линейные функции часто используются в краткосрочных и среднесрочных экономических моделях.

б) степенные производственные функции

 ,

,

.

Параметры  и  выражают эластичность уровня производства  по отношению к факторам  и , то есть показывают относительный прирост продукции, связанный с относительным приростом  и .

 - объем трудовых ресурсов в натуральном количестве,

 - число рабочих, число человеко-дней,

 - выпуск продукции в стоимостном или натуральном виде.

в) более сложные производственные функции CES

,

где  - параметр, выражающий эластичность замены ОФ и занятости.

2. Предполагается, что производственные факторы удовлетворяют аксиоме. Существует подмножество производства страны затрат, называемое экономической областью , в которой увеличение любого вида затрат не приводит к уменьшению выпуска. Если  - две точки этой области, то  влечет .

Эта аксиома утверждает, что производственные факторы не какая-то совершенно абстрактная функция, придуманная теоретиками - математиками.

Она отражает утверждение, пусть и не на всей своей области определения, а только на ее части: в мало-мальски разумной экономике увеличение затрат не может привести к уменьшению выпуска.

 В дифференциальной форме это выражается в том, что в этой области первые частные производные функции неотрицательны:  - непрерывная и дифференцируемая

.

.

Эти производные называются предельными продуктами.

Можно составить производственные функции данного производства даже ничего не зная о производстве. Надо только поставить у возможного производства счетчик (человека на какое-то автоматическое увеличение), который будет фиксировать увеличиваемые ресурсы и  - количество продукции, которую производство произвело. Если накопить достаточно много такой статической информации, учесть работу производства в различных режимах, то можно прогнозировать выпуск продукции, зная объем ввезенных ресурсов, а это и есть производственная функция.

3 Понятие «однородность производственной функции» включает в себя следующее ее свойство: равномерное увеличение всех производственных факторов вызывает пропорциональное увеличение продукта. Выразим это математически:

Функция  однородна в степени h. если

.

Таким образом, когда каждая независимая переменная принимает значения , значение функции  возрастает в  раз.

Величина  показывает степень использования производственных факторов или их эффективность. В случае, когда , эффективность производственных факторов будет равна 1, при  говорят, что производственные факторы обладают растущей эффективностью и соответственно при  эффективность факторов снижается