Навигация
Формальная постановка задачи
2. Формальная постановка задачи
Приведем еще раз задачу данной курсовой работы: используя профиль преимуществ избирателей, определить единственного победителя из множественного числа заданных. Должна существовать возможность проверки корректности задания профиля. Ограничениями на задачу является отсутствие безразличия и ранжировки кандидатов в строгом порядке. Опишем методы голосования, которые могут использоваться для решения данной задачи и наведем ряд основных определений и теорем.
Правило относительного большинства. Каждый избиратель отдает свои голос наилучшему для себя кандидату. Избирается кандидат, упомянутый в наибольшем количестве бюллетеней. Это правило может противоречить мнению большинства (см. 1, пример 9.1).
Определение 2.1. Правило Борда. Каждый избиратель сообщает свои преимущества, ранжируя р кандидатов от лучшего к хуже (безразличие запрещается). Кандидат не получает очков за последнее место, получает одно очко за предпоследнее и так далее, получает р-1 очков за первое место. Побеждает кандидат с наибольшей суммой очков. Он называется победителем по Борду.
Мы не уточняем, что делать при равенстве очков.
Определение 2.2. Для заданного профиля преимуществ победителем по Кондорсу называется кандидат а, что побеждает любого другого кандидата при парном сравнении по правилу большинства:
для всякого b¹а избирателей, которые считают а лучшим за b, больше, чем тех, кто считает, что b лучшим за а.
Зажиточное по Кондорсу правило выбирает победителя по Кондорсу, если такой существует.
Отсутствие победителя по Кондорсу является знаменитым "парадоксом голосования". Как часто может наблюдаться парадокс голосования? В общем случае вероятность p(p, n) того, что победителя по Кондорсу не существует при р кандидатах и n избирателях, растет по р и растет по числу избирателей от n к n+2. Это может быть проверено на основе вычисления p(п, р)для малых значений n и р, но в общем случае это утверждение остается недоказанным предположением.
Парадокс голосования становится почти достоверным событием, когда число кандидатов становится достаточно большим при фиксированном n. Если число избирателей становится достаточно большим при фиксированном р, то предельная вероятность p(p) может быть оценена по Фишберну [1984]:
![]()
которая справедлива с точностью до половины процента при р£50.
Определение 2.3. Правила голосования с подсчетом очков.
Фиксируем последовательность вещественных чисел, которая не спадает
s0£s1£…£sp-1 при s0<sp-1.
Избиратели ранжируют кандидатов, причем s0 очков дается за последнее место, s1 - за предпоследнее и так далее. Избирается кандидат с максимальной суммой очков.
Определение 2.4. Правило Копленда. Сравним кандидата а с любым другим кандидатом х. Начислим ему +1, если для большинства а лучше за х, -1, если для большинства х лучше за а, и 0 при равенстве. Суммируя общее количество очков по всем х, х¹а, получаем оценку Копленда для а. Избирается кандидат, названный победителем за Коплендом, с наивысшей из таких оценок.
Определение 2.5. Правило Симпсона. Рассмотрим кандидата а, любого другого кандидата х и обозначим через N(а,x) число избирателей, для которых а лучше за х. Оценкой Симпсона для а называется минимальное из чисел N(а,x) по всем х, х¹а. Избирается кандидат, названный победителем по Симпсону, с наивысшей такой оценкой. Оба этих правила зажиточные по Кондорсу.
Оптимальность по Парето. Если кандидат а для всех лучший от кандидата b, то b не может быть избранным.
Анонимность. Имена избирателей не имеют значения: если два избирателя поменяются голосами, то результат выборов не изменится.
Нейтральность. Имена кандидатов не имеют значения. Если мы поменяем местами кандидатов а и b в преимуществе каждого избирателя, то результат голосования изменится соответственно (если раньше выбирался а, то теперь будет выбираться b и наоборот; если выбирался некоторый х, отличающийся от а и b, то он же и будет выбран).
Правила Копленда и Симпсона оптимальные по Парето, анонимные и нейтральные, если мы рассматриваем их как отображения, которые ставят в соответствие каждому профилю преимуществ подмножество победителей. Анонимность и нейтральность очевидны. Проверить, что множественные числа победителей по Борду (Копленду, Симпсону) содержат только оптимальные по Парето результаты, достаточно просто. Да, оценка Симпсона кандидату, что доминируется по Парето, равняется нулю, а для оптимального по Парето кандидата она позитивна.
Монотонность. Допустим, что а выбирается (среди победителей) при данном профиле и профиль изменяется только так, что положение а улучшается, а относительное сравнение пары любых других кандидатов для любого избирателя остается неизменным. Тогда а как и раньше будет избран (опять среди победителей) для нового профиля.
Все правила подсчета очков, а также правила Копленда и Симпсона являются монотонными.
Относительное большинство с выбыванием. В первом раунде каждый избиратель подает один голос за одного кандидата. Если кандидат набирает суровое большинство голосов, то он и избирается. В противном случае во втором туре проводится голосование по правилу большинства с двумя кандидатами, которые набрали наибольшее количество голосов в первом туре.
Сторонники этого метода подтверждают, что он почти так же простой, как и правило относительного большинства (избирателям не нужно сообщать полное ранжирование кандидатов), и исключает расточительные выборы. При обычном правиле относительного большинства, если я голосую за кандидата, который получает маленькую поддержку, то мой голос будет напрасным. Однако при выбывании у меня есть еще один шанс повлиять на результат.
Однако этот метод не является монотонным, как показывают такие два профиля с 17 избирателями:
| Профиль А | Профиль B | ||||||
| 6 | 5 | 4 | 2 | 6 | 5 | 4 | 2 |
| a | c | b | b | a | c | b | a |
| b | a | c | a | b | a | c | b |
| c | b | a | c | c | b | a | c |
При профиле А во второй тур проходять а и b и выигрывает а (11 голосов против 6). Профиль В такой же за одним исключением. У двух избирателей преимущество b>a>с изменяется на преимущество а>b>с, то есть для них теперь а лучше b. Теперь во второй тур проходять а и с, причем выигрывает с (9 голосов против 8). Таким образом, улучшение позиции кандидата а приводит к его поражению!
Метод альтернативных голосов. Исключим сначала тех, кто получил наименьшее количество голосов. Потом посчитаем голоса для кандидатов, которые остались, и опять исключим неудачников. Будем повторять эту операцию до тех пор, пока не останется один кандидат (или множественное число кандидатов с ровным числом голосов).
Здесь главное внимание уделяется потому, чтобы не потерять никаких голосов и каждому дать шанс поддержать кандидата, который нравится больше всего. В этом подходе повторно используются методы подсчета очков для исключения кандидатов-неудачников. К сожалению, любое правило, основанное на последовательном исключении по методу подсчета очков, должно нарушать свойство монотонности для некоторых профилей.
Пополнение (однозначные правила голосования). Две группы избирателей N1, N2, что не пересекаются, имеют дело с тем же множественным числом А кандидатов. Пусть избиратели N1 и N2 выбирают того же кандидата а. Тогда избирателе N1ÈN2 также изберут а из А.
Это свойство является очень обоснованным, когда единственный избирательный орган разбит на большое количество подмножеств, как в случае региональных ассамблей и подкомитетов.
Пополнение (отображение голосования). Две группы избирателей N1, N2, что не пересекаются, имеют дело с тем же множественным числом А кандидатов. Пусть избиратели Ni избирают подмножество Вi з А при i=1,2. Если В1 и B2 пересекаются, то избирателе N1ÈN2 изберут В1ÇB2 как множественное число наилучших для себя результатов.
Теорема 2.1 (Янг [1975])
(а) Все отображения голосования, основанные на подсчете очков (подмножества кандидатов, которые выбирают, с наибольшим суммарным количеством очков), удовлетворяют аксиоме пополнения. Если при равенстве очков выбор проводится на основе фиксированного порядка на А, то соответствующие правила голосования также удовлетворяют аксиоме пополнения.
(b) Не существует зажиточного по Кондорсу правила голосования (или отображение голосования), которое бы удовлетворяло аксиоме пополнения.
Аксиома участия. Пусть кандидат а выбирается из множественного числа А избирателями из N. Рассмотрим дальше избирателя и за N. Тогда избиратели из NÈ{i} должны избрать или а, или кандидата, что для агента I и строго лучше а.
Значит, что если дополнительный голос действительно изменяет результат выборов, то это может быть только на руку "ключевому" избирателю.
Теорема 2.2 (Мулен [1986с])
(a) Для всех правил голосования с подсчетом очков, когда при равенстве очков выбор осуществляется с помощью заданного порядка на А, выполняется аксиома участия.
(b) Если А состоит хотя бы из четырех кандидатов, то ни одно зажиточное по Кондорсу правило голосования не удовлетворяет аксиоме участия.
Непрерывность. Пусть избиратели из N1 избирают кандидата а из A, а группа N2, которая не пересекается из N1, избирает другого кандидата b. Тогда существует достаточно большое число m дублей группы избирателей N1, такое что комбинированная группа избирателей (mN1)ÈN2 выберет а.
Теорема 2.3 (Янг [1975]).
Отображение голосования основано на методе подсчета очков (определение 2.3 без фиксации правила для случая равенства очков) тогда и только затем, когда оно удовлетворяет таким четырем свойствам:
анонимность, нейтральность
аксиома пополнения и непрерывность.

Голосование с последовательным исключением.
Сначала по правилу большинства исключается или а, или b, потом по правилу большинства проводится сравнение победителя первого раунда и с и так далее. В случае равенства проигрывает нижний кандидат.
В этом процессе поправок пусть а - поправка, b - поправка к поправке, с - исходное предложение, d - status quo.
Этот метод удовлетворяет аксиоме по Кондорсу: если а - победитель по Кондорсу, то он выигрывает. В действительности возможность при сравнениях по правилу большинства справедливая в более широком содержании.
Возможность по Смиту. Если множественное число А кандидатов разбивается на два подмножества В1, B2, что не пересекаются, и каждый кандидат b1ÎВ1 выигрывает (за суровым большинством) у любого кандидата b2ÎВ2, то должен быть избран результат из В1.
С другой стороны, голосование при последовательном исключении очевидно не является нейтральным. Порядок исключений, конечно, влияет на результат.
Правило равномерного исключения. Сначала по правилу большинства выравниваются пары а из b и с из d. Победители встречаются в финале, где сравниваются по правилу большинства. В случае равенства выбирается кандидат, который идет раньше по алфавиту.
Это - опять зажиточный по Кондорсу метод. Более того, для избрания каждому кандидату х нужно победить в двух сравнениях по правилу большинства. Допустимо сначала, что равенства при сравнении с этими двумя кандидатами нет (х выигрывает для сурового большинства). Тогда х не может доминироваться по Парето некоторым кандидатом в, иначе b был бы победителем по Кондорсу. Следовательно, метод равномерного исключения выбирает оптимальный по Парето результат в случае, когда при бинарных выборах нет равенств. Однако если равенства возможны, то оптимум по Парето может нарушаться.
Бинарным деревом на А есть такое конечное дерево, в котором каждой нефинальной вершине (включая начальную) отвечают ровно две следующие, а каждой финальной вершине (у которой нет следующих) приписан кандидат (элемент из A), причем каждый кандидат появляется по крайней мере в одной финальной вершине.
Среди бинарных деревьев самыми простыми являются те, в которых каждый кандидат приписан ровно одной вершине. Назовем их деревьями без повторных исключений.
Лемма 2.1 (а) Если А состоит из трех кандидатов, то дерево после последовательного исключения является единственным безповторним деревом. Соответствующее правило голосования оптимально за Парето (при нашем условии, что все сравнения по большинства суровые). (b) Если А состоит из четырех кандидатов, то есть только два безповторних деревья: последовательное исключение и ривнобижне исключение. Первое из них нарушает оптимум за Парето, а последнее - нет. (c) Если А содержит пять или больше кандидатов, то любое исключение по безповторному дереву приводит к избранию кандидата для некоторых профилей, во что доминируется по Парето.
Существует бинарное дерево, определенное для произвольного количества участников, что позволяет избежать обеих этих опасностей. Соответствующие последовательные исключения порождают оптимальное по Парето, анонимное и монотонное правило голосования. Это дерево называется деревом многоэтапного исключения.
Для каждого конкретного упорядочения кандидатов существует по одному такому дереву. Обозначим через Гp(1,2,... ,р) дерево, которое отвечает порядку A={1,2...,р}. Определим его индуктивно по размеру А:
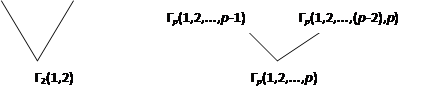
Да, для трех и четырех кандидатов получаем:
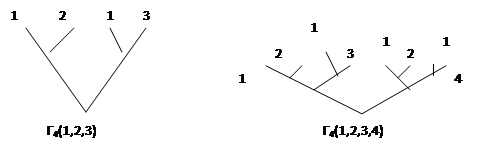
При р кандидатах образуются 2p-l финальные вершины; кандидат 1 приписанный 2p-2 финальным вершинам, а кандидат р только одной. Тем не меньше для избрания даже кандидату р нужно победить в р-1 дуэлях (хотя ему возможно придется по нескольку раз столкнуться с тем же оппонентом). Хотя дерево многоэтапного исключения большое, его решение (то есть вычисление кандидата, который выигрывает) может быть получено с помощью очень простого алгоритма.
Теорема 2.4 (Шепсл и Вейнгаст [1984]).
Заданы дерево многоэтапного исключения Гp(1,2,... ,р и профиль преимущества, которое отвечает мажоритарному турниру Т. Кандидат а* может быть найден по такому алгоритму:
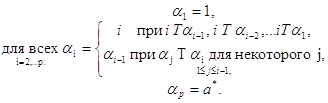 (12)
(12)
Следствие теоремы 2.4.
Кандидат а, что выбирается по дереву многоэтапного исключения с турниром Т, удовлетворяет условию:
для любого bÎА, b¹а:
{аТb} і/или {для некоторого с, аТс і сTb}. (14)
В частности, а оптимальный по Парето. Более того, дерево многоэтапного исключения порождает монотонный метод голосования.
Среди зажиточных по Кондорсу правил голосования мы обнаружили три метода, которые удовлетворяют основным требованиям оптимума по Парето, анонимности и монотонности: множественное число победителей по Копленду, множественное число победителей по Симпсону и дерево многоэтапного исключения. Первые два нейтральные, но могут выделять несколько победителей (дополнительное правило при равенстве очков нарушит нейтральность). Заметим, что победитель при многоэтапном исключении находится быстрее, поскольку алгоритм (12) в среднем нуждается в сравнении не больше половины от всех p(p-l) пар. В то же время для определения победителей по Копленду и Симпсону нужно провести весь турнир сравнений по правилу большинства.
Похожие работы
... Поэтому целесообразно разработать предназначенный для поддержки проведения экспертных исследований АРМ "МАТЭК" ("Математика в экспертизе") на базе РС фирмы "Apple" с использованием современных достижений в области теории и практики экспертных оценок, в области прикладной математической статистики, прежде всего статистики объектов нечисловой природы. Список литературы 1. Орлов А.И. Допустимые ...
... применение количественных методов как при организации экспертизы, так и при оценке суждений экспертов и формальной групповой обработке результатов. Эти две особенности отличают метод экспертных оценок от обычной давно известной экспертизы, широко применяемой в различных сферах человеческой деятельности. Экспертные коллективные оценки широко использовались в государственном масштабе для решения ...
... элемента на качество принимаемых управленческих решений - одна из главных задач оптимизации процессов принятия решений в управлении общественным производством. Одним из условий преодоления субъективизма при подготовке управленческих решений являются методы исследования операций, методы экспертных оценок. Процедура выработки управленческих решений, являясь сложным логико-мыслительным процессом, ...
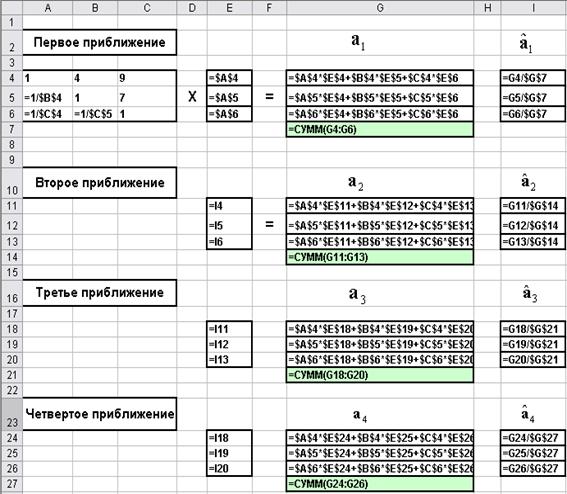
... : Подставляя (6.7) в (6.8) получим более удобное для использования соотношение: , (6.9) где квадратная симметрическая матрица называется матрицей взаимосвязи экспертных оценок и определяется равенством: (6.10) Для иллюстрации работы вышеописанного алгоритма приведем простой пример. экспертиза объект оценка Пример 1 ...



0 комментариев