Навигация
5.3 Инструкция пользователю
Данная программа предназначенная для определения победителя выборов по правилам Копленда и Борда и сравнение полученных результатов.
В начале работы программы пользователь может выбрать, просматривать ли результаты решения контрольного примера, вносить ли собственные данные. В обоих случаях определяются победители за Коплендом и Борда.
Сначала работники избирательного органа вносят общую информацию: количество избирателей в данном округе то количество кандидатов. Дальше заносятся имена кандидатов и указывается способ заноса профилей преимуществ: каждым избирателем отдельно или работниками избирательного округа. В последнем случае информация сгруппирована (аналогично к контрольному примеру).
Внизу екрана выводятся имена всех кандидатов. Каждый избиратель (работник ли избирательного округа) вносит профиль преимуществ, располагая кандидатов в строго определенном порядке.
Для каждого избирателя не допускается случаев безразличия; кроме того, кандидаты должны быть строго ранджовани (то есть каждый из них занимает свое место в преимуществе избирателя, и на одном уровне не могут находиться два кандидата). Имена кандидатов, которые заносятся избирателями, повинны совпадать с именами, указанными в начале заполнения информации.
После заноса всех этих данных выдается результат работы программы.
Сначала выводится победитель Копленда и указывается, определен ли он с сохранением нейтральности. Для победителя указывается его оценка. В противном случае выводится множественное число победителей (кандидатов, сумма глазков которых равняется максимальной оценке).
Аналогично определяется победитель Борда.
Как будет показано в контрольном примере, оценки кандидатов, полученных по правилам Борда и Копленда, могут ранджуватись в противоположном порядке.
6. Контрольный пример
Пусть дан следующий профиль для 9 избирателей и 5-ти кандидатов:
| 1 | 4 | 1 | 3 |
| a b c d e | c d b e a | e a d b c | e a b d c |
В каждом столбце кандидаты расположенные в порядке уменьшения их значимости для каждой группы избирателей. То есть, для первого столбца можно определить преимущества следующим образом: группа избирателей, которая состоит из одного лица, считает кандидата а наилучшим. На втором месте они ставят кандидата b, на третьем месте c и т.д.
Продемонстрируем решение контрольного примера по правилу Копленда. Определяем оценку Копленда.
Кандидат а является лучшим за b для 1+1+3 избирателей, а для 4-х избирателей кандидат b является лучшим за а. Определим такие преимущества для каждого кандидата, сравним его со всеми другими.
| ab – 5 ac – 5 ad – 5 ae – 1 | ba – 4 ca – 4 da – 4 ea – 8 | bc – 5 bd – 4 de – 5 | cb – 4 db – 5 eb – 4 | cd – 5 ce – 5 | dc – 4 ec – 4 | de – 5 | ed – 4 |
Определим оценку Копленда для каждого кандидата. Кандидат а является лучшим за b (добавляем +1); он также является лучшим за c и d (добавляем два разы +1) и худшим за e (добавляем –1). Следовательно, оценка Копленда для а ровна 2.
Найдем оценку для других кандидатов.
a=+1+1+1-1=2
b=-1+1-1+1=0
c=-1-1+1+=0
d=-1+1-1+1=0
e=+1-1-1-1=-2
Среди полученных оценок определяем максимальную. Как видим, она равняется 2 и принадлежит кандидату а. Следовательно, а – победитель Копленда.
Если бы у нас получились два кандидата с максимальной оценкой, например b и f, мы бы избрали кандидата b, так как он расположен ближе за алфавитом.
Для этого же профиля найдем победителя Борда.
Следовательно, получаем такие оценки:
a=1*4+4*0+1*3+3*3=16
b=3*1+2*4+1*1+2*3=18
c=2*1+4*4+0+0=18
d=1*1+4*3+2*1+1*3=18
e=1*4+1*4+3*4+0=20
Победителем за Борда является кандидат е.
Как видим, оценки Борда ранжируют кандидатов в порядке, противоположном до того, который получается по оценкам Копленда.
Выводы
Данная курсовая работа была посвящена обзору методов голосования большинством голосов. Была проведена сравнительная характеристика каждого из методов и из их множественного числа избраны наилучшие. К ним относятся:
1. зажиточные за Кондорсе правила Копленда и Симпсона, дерево многоэтапного исключения;
2. один из методов подсчета очков – правило Борда.
Все эти правила удовлетворяют условиям оптимума по Парето, монотонности и анонимности. Кроме того, правило Борда удовлетворяет также аксиоме участия и пополнения.
Для программной реализации были избраны методы Копленда и Борда.
Результаты работы программы продемонстрированы на контрольном примере.
Список литературы
1. Мулен Э. "Кооперативное принятие решений: Аксиомы и модели" – Москва, Мир, 1991.
2. Миркин Б. Проблема группового выбора. – Москва, Наука, 1974.
3. Льюс Р.Д., Райфа Х. Игры и решения. М.: ИЛ, 1961.
4. Антонов А. В. "Системный анализ", М.-2004г.
5. Ларичев О.И. Наука и искусство принятия решений. – М: Наука, 1979. – 200 с.
6. Макаров И.М. Теория выбора и принятия решений. – М.: Наука,1987. – 350 с.
7. Кузнецов А.В., Сакович В.А., Холод Н.И. "Высшая математика. Математическое программирование ", Минск, Вышейшая школа, 2001г.
8. Красс М.С., Чупрынов Б.П. "Основы математики и ее приложения в экономическом образовании", Издательство "Дело", Москва 2001г.
9. В.И. Ермаков "Общий курс высшей математики для экономистов", Москва, Инфра-М, 2000г.
10. Теория прогнозирования и принятия решений. М:1989. 160 стр.
Дополнения
Программа
uses wincrt;
label в, z;
type mas = string[6];
type ball =array[1..10] of shortint;
var N: byte; {кол-во избирателей}
M: byte; {кол-во кандидатов}
s: byte; {кол-во групп}
rang: array[1..10,1..100] of mas; {профиль преимуществ}
к,i,j,l,r,contrl: byte;
а,b: byte; {для проведения парных сравнений}
kopl: ball; {массив оценок Копленда}
vybor1, vybor2: mas;
bord: ball; {массив оценок Борда}
name: array[1..10] of mas; {массив имен кандидатов}
many: array[1..100] of byte; {массив групп избирателей}
n1: array[1..10] of mas;
c: char;
{данные контрольного примера}
{---------------------------}
procedure example;
var и, j: byte;
begin
clrscr; M:=5; n:=9; s:=4;
name[1]:='a'; name[2]:='b'; name[3]:='c'; name[4]:='d'; name[5]:='e';
many[1]:=1; many[2]:=4; many[3]:=1; many[4]:=3;
rang[1,1]:='a'; rang[1,2]:='c'; rang[1,3]:='e'; rang[1,4]:='e';
rang[2,1]:='b'; rang[2,2]:='d'; rang[2,3]:='a'; rang[2,4]:='a';
rang[3,1]:='c'; rang[3,2]:='b'; rang[3,3]:='d'; rang[3,4]:='b';
rang[4,1]:='d'; rang[4,2]:='e'; rang[4,3]:='b'; rang[4,4]:='d';
rang[5,1]:='e'; rang[5,2]:='a'; rang[5,3]:='c'; rang[5,4]:='c';
gotoXY(15,1);
writeln; writeln('Число избирателей: ', N);
writeln('Число кандидатов: ', M);
writeln('Профиль преимуществ:');
for i:=1 to 40 do
write('-');
writeln; write('Число избирателей ');
gotoXY(19,7);
for i:=1 to s do
write(many[i] ' ');
writeln; gotoXY(19,9);
for i:=1 to M do
begin
for j:=1 to s do
write(rang[і,j] ' ');
gotoXY(19, 9+i);
end;
gotoXY(1,15);
end;
{---------------------------}
{проверяет правильность ввода варианта выбора} procedure right;
label l;
begin
l: readln(c);
if (c<>'0') and (c<>'1') then
begin
write('Повторите попытку: ');
goto l;
end;
end;
{---------------------------}
{выводит список имен кандидатов}
procedure help;
var x,y,i: byte;
begin
x:=WhereX;
y:=WhereY;
gotoXY(1,24);
write('Имена кандидатов: ');
for i:=1 to M do
if i<>M then write(name[i] ', ')
else write(name[i]);
gotoXY(x,y);
end;
{---------------------------}
{определение победителя выборов}
procedure victory(v: ball; s: string);
var max, t: shortint;
hl: array[1..10] of byte;
begin
{определение максимальной оценки}
help;
max:=v[1];
for i:=1 to M do
if max<v[i] then
max:=v[i];
t:=1;
{определение кандидатов с максимальной оценкой}
for i:=1 to M do
if (v[i]-max)=0 then
begin
hl[t]:=i;
t:=t+1;
end;
if (t-1)=1 then
begin
write('Победитель за ', s ' с сохранением нейтральности: ');
writeln(name[hl[1]]); writeln('Сумма очков - ', max);
end
else
begin
vybor1:=name[hl[1]];
for i:=2 to t-1 do
if name[hl[i]]<vybor1 then
vybor1:=name[hl[i]];
write('Победитель за ', s ' без сохранения нейтральности: ');
writeln(vybor1);
writeln('Сумма очков - ', max);
writeln('избранный из множественного числа наилучших:');
for i:=1 to t-1 do
writeln(name[hl[i]]);
end;
end;
{---------------------------}
{основная программа}
begin
gotoXY(21,1); writeln('Определение победителя выборов');
writeln; writeln('Запуск контрольного примера - 1; Самостоятельное внесение профиля 0');
right;
if c='1' then
begin
example;
help;
goto z;
end
else clrscr;
write('Введите количество кандидатов: ');
readln(M);
write('Введите количество избирателей: ');
readln(N);
writeln('Введите имена кандидатов');
for i:=1 to M do
begin
write('Кандидат ', и ': ');
readln(name[i]);
end;
writeln('Как будет осуществляться занос
информации?');
write('1- отдельными избирателями, 0- комитетом: ');
right;
if c='1' then
for i:=1 to N do
many[i]:=1;
clrscr; writeln('Введите профиль преимуществ');
s:=1; contrl:=0;
while contrl<>N do
begin
if c='1' then writeln('Избиратель ', s)
else writeln('Группа ', s);
for i:=1 to m do
n1[i]:='';
help;
for j:=1 to M do
begin
y:readln(vybor1);
{проверка на корректность введенного профиля}
r:=0; a:=0; b:=0;
n1[j]:=vybor1;
for l:=1 to M do
begin
if vybor1=name[l] then
begin
b:=1;
for a:=1 to M do
{такое имя уже было введено в данном профиле}
if (vybor1=n1[a]) and ((a-j)<>0) then r:=1;
end;
{имя введенного кандидата не совпадает с ни одним из списка}
if (vybor1<>name[l]) and (l=M) and
(b<>1) then r:=1;
end;
if r=1 then
begin
n1[j]:='';
writeln('Внимательно вводите имена кандидатов');
goto в;
end
else rang[j,s]:=vybor1; {профиль корректен}
end;
if c='0' then
begin
writeln('Количество избирателей в
группе ', s);
readln(many[s]);
contrl:=contrl+many[s];
end
else
contrl:=contrl+1;
s:=s+1;
clrscr;
end; {while}
{Определение оценок Копленда}
z: contrl:=1;
while contrl<=M do
begin
k:=contrl+1;
vybor1:=name[contrl]; vybor2:=name[k];
while k<=M do
begin
i:=1; a:=0; b:=0;
while i<=s do
begin
for j:=1 to M do
if rang[j,i]=vybor1 then l:=j
else
if rang[j,i]=vybor2 then r:=j;
if l<r then a:=a+many[i]
else
if l>r then b:=b+many[i];
i:=i+1;
end;
if a>b then
begin
kopl[contrl]:=kopl[contrl]+1;
kopl[k]:=kopl[k]-1;
end
else
if a<b then
begin
kopl[k]:=kopl[k]+1;
kopl[contrl]:=kopl[contrl]-1;
end;
k:=k+1;
vybor2:=name[k];
end; {while по к}
contrl:=contrl+1;
end; {while по contrl}
{определение оценок Борда}
for i:=1 to s do
for j:=1 to M do
begin
for k:=1 to M do
if rang[j,i]=name[k] then r:=k;
bord[r]:=many[i]*(M-j)+bord[r];
end;
victory(kopl, 'Коплендом');
writeln ('Нажмите любую клавишу
'); readkey; writeln;
victory(bord, 'Борда');
end.
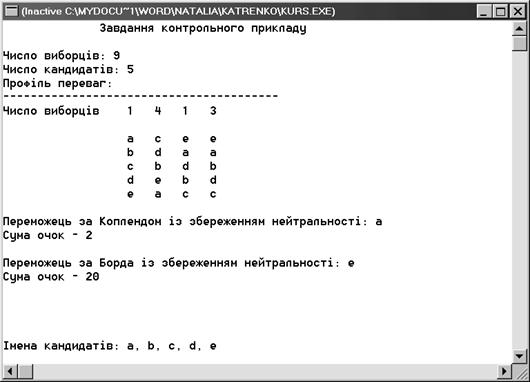
Результаты работы программы
Самостоятельное внесение профиля.
Введите количество кандидатов: 5
Введите количество избирателей: 9
Введите имена кандидатов
Кандидат 1: а
Кандидат 2: b
Кандидат 3: c
Кандидат 4: d
Кандидат 5: е
Как будет осуществляться занос
информации?
1-отдельными избирателями, 0 –
комитетом: 0
Введите профиль преимуществ
Группа 1
a
b
c
d
e
Количество избирателей в группе 1: 1
Группа 2
c
d
b
e
a
Количество избирателей в группе 2: 4
Группа 3
e
a
d
b
c
Количество избирателей в группе 3: 1
Группа 4
e
a
b
d
c
Количество избирателей в группе 4: 3
Победитель по Копленду с сохранением нейтральности – а
Сумма очков – 2
Победитель по Борду с сохранением нейтральности – е
Сумма очков – 20
Результаты работы программы
Похожие работы
... Поэтому целесообразно разработать предназначенный для поддержки проведения экспертных исследований АРМ "МАТЭК" ("Математика в экспертизе") на базе РС фирмы "Apple" с использованием современных достижений в области теории и практики экспертных оценок, в области прикладной математической статистики, прежде всего статистики объектов нечисловой природы. Список литературы 1. Орлов А.И. Допустимые ...
... применение количественных методов как при организации экспертизы, так и при оценке суждений экспертов и формальной групповой обработке результатов. Эти две особенности отличают метод экспертных оценок от обычной давно известной экспертизы, широко применяемой в различных сферах человеческой деятельности. Экспертные коллективные оценки широко использовались в государственном масштабе для решения ...
... элемента на качество принимаемых управленческих решений - одна из главных задач оптимизации процессов принятия решений в управлении общественным производством. Одним из условий преодоления субъективизма при подготовке управленческих решений являются методы исследования операций, методы экспертных оценок. Процедура выработки управленческих решений, являясь сложным логико-мыслительным процессом, ...
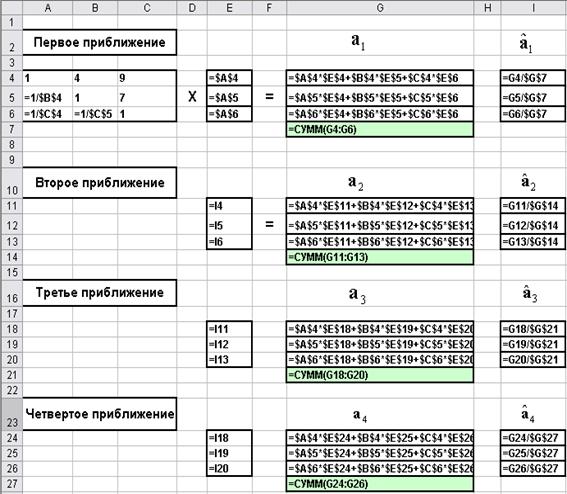
... : Подставляя (6.7) в (6.8) получим более удобное для использования соотношение: , (6.9) где квадратная симметрическая матрица называется матрицей взаимосвязи экспертных оценок и определяется равенством: (6.10) Для иллюстрации работы вышеописанного алгоритма приведем простой пример. экспертиза объект оценка Пример 1 ...



0 комментариев