Навигация
ОПИС І РОЗРОБКА НОВОГО МАТЕМАТИЧНОГО МЕТОДУ ПРОГНОЗУВАННЯ КРОС-КУРСІВ
3. ОПИС І РОЗРОБКА НОВОГО МАТЕМАТИЧНОГО МЕТОДУ ПРОГНОЗУВАННЯ КРОС-КУРСІВ
3.1 Математична постановка задачі
Розгляд графіка будь якої валюти показує, що він являє собою суму синусоїд з різним періодом (рис. 3.1).
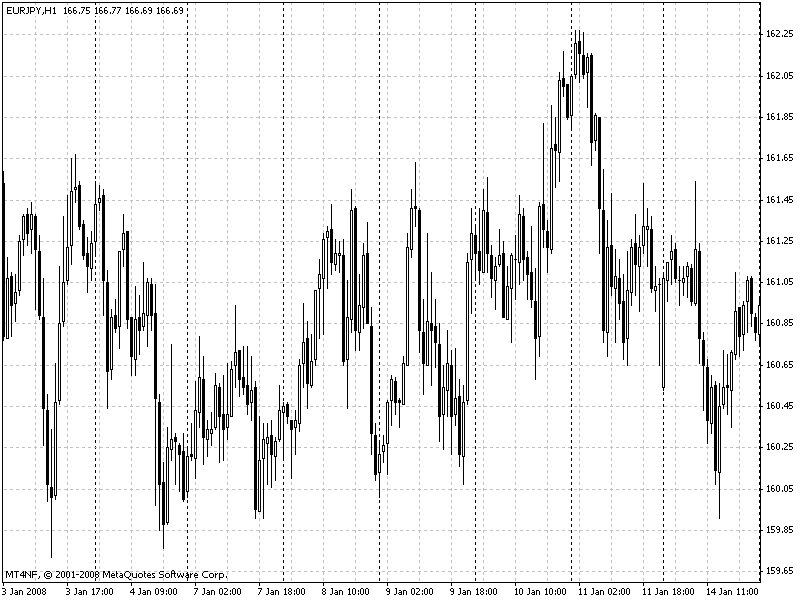
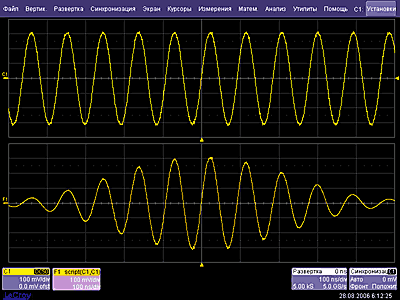
Рис. 3.1. – Співвідношення хвильоподібності крос-курсу з синусоїдою
Дослідження впливу зміни цих проміжків часу, розділених на амплітуди характеристичних частот, повинно забезпечити покращення прогнозування, – перетворення Фур’є (2.4) і методів нелінійно регресійного аналізу(2.2).
3.2 Проведення розрахунків
Проведемо дослідження графіка зміни крос-курсу EUR/JPY в наступних періодах:
25.01.2007 – 5.02.2007
6.02.2007 – 15.02.2007
16.02.2007 – 23.02.2007
26.02.2007 – 5.03.2007
6.03.2007 – 15.03.2007
16.03.2007 – 25.03.2007
26.03.2007 – 5.04.2007
6.04.2007 – 15.04.2007
16.04.2007 – 25.04.2007
26.04.2007 – 4.05.2007
06.05.2007 – 15.05.2007
16.05.2007 – 25.05.2007
Таким чином утворено 12 вибірок по 240 точок у кожній. Вихідні дані розміщені в таблиці 3.1.
Таблиця 3.1.
Вихідні дані до першого періоду (25.01.2007 – 5.02.2007)
| Дата | Час | Відкриття | Максимум | Мінімум | Закриття |
| 25,01,2007 | 0:00 | 157,15 | 157,18 | 156,92 | 156,94 |
| 25,01,2007 | 1:00 | 156,95 | 156,98 | 156,66 | 156,68 |
| 25,01,2007 | 2:00 | 156,67 | 156,83 | 156,65 | 156,7 |
| 25,01,2007 | 3:00 | 156,72 | 156,77 | 156,42 | 156,46 |
| 25,01,2007 | 4:00 | 156,44 | 156,49 | 156,06 | 156,1 |
| 25,01,2007 | 5:00 | 156,09 | 156,38 | 156,06 | 156,22 |
| 25,01,2007 | 6:00 | 156,21 | 156,26 | 156,03 | 156,03 |
| 25,01,2007 | 7:00 | 156,02 | 156,27 | 155,75 | 155,97 |
| 25,01,2007 | 8:00 | 155,98 | 156,23 | 155,85 | 156,2 |
| 25,01,2007 | 9:00 | 156,21 | 156,59 | 156,08 | 156,5 |
| ... | ... | ... | ... | ... | ... |
| 05,02,2007 | 19:00 | 155,6 | 155,66 | 155,49 | 155,5 |
| 05,02,2007 | 20:00 | 155,52 | 155,54 | 155,46 | 155,47 |
| 05,02,2007 | 21:00 | 155,49 | 155,61 | 155,47 | 155,55 |
| 05,02,2007 | 22:00 | 155,54 | 155,63 | 155,5 | 155,63 |
| 05,02,2007 | 23:00 | 155,61 | 155,63 | 155,55 | 155,58 |
Для кожної вибірки розрахуємо спектральну щільність за (2.4) із застосуванням програми Statistica 6.0 (рис. 3.2.). Приклад такого графіка для 2-го та 8-го періодів показано на рис. 3.3..
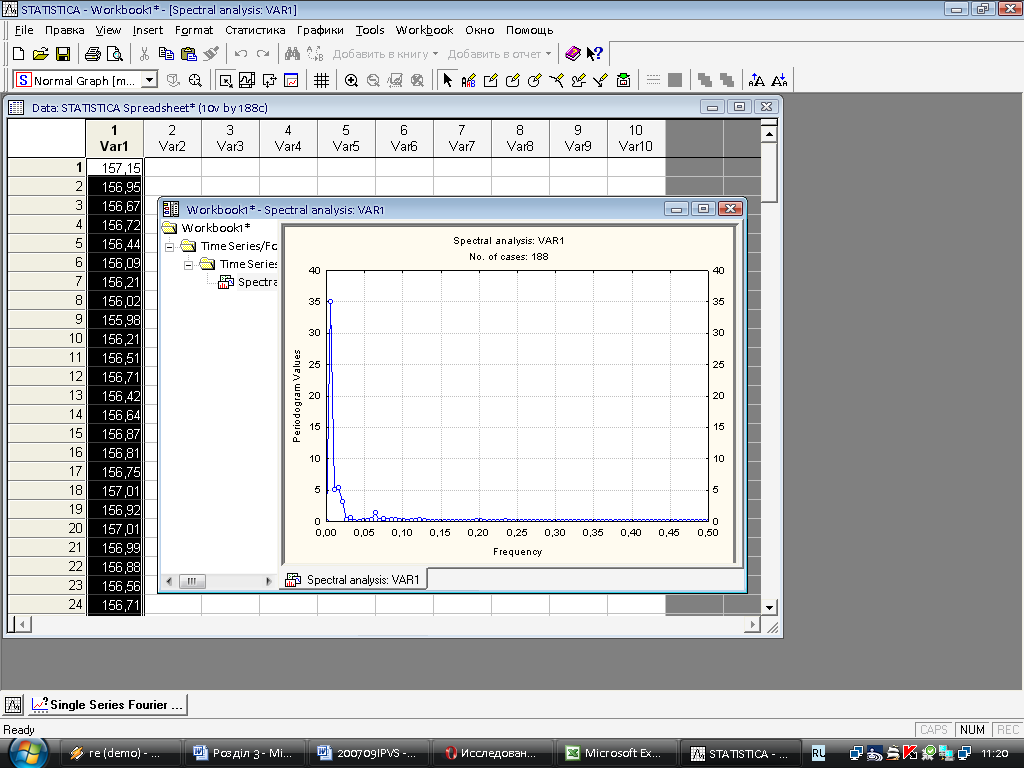
Рис. 3.2. – Інтерфейс програми «Statistica 6.0»
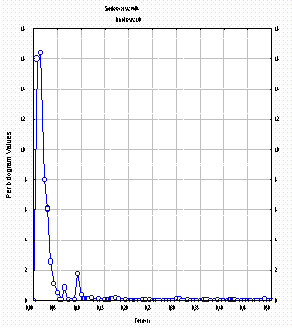
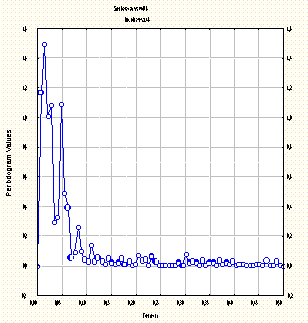
Рис. 3.3. – Графік спектральної щільності
Проаналізувавши 12 періодів на графіках спектральної щільності ми бачимо, що вини мають одну, дві або і три амплітуди коливання але всі вони схожі однією чітко вираженою амплітудою з періодом f = 0,02.
Тепер, знайшовши графічну закономірність за допомогою перетворення Фур’є, – а це є ключовим моментом в прогнозуванні економічних періодичних процесів, необхідно описати закономірність математично. Виконаємо математичний опис знайдених закономірностей за допомогою методів математичного програмування (2.2).
Представимо математичну модель в виді таблиці 3.2..
Таблиця 3.2.
Математична модель
| № періоду | t | A f = 0,2 | A | ∆ = (A f = 0,2 - A)2 | |||
| 1 | 31.01.2007 | 2,8 | 1,0 | 1,8 | |||
| 2 | 20.02.2007 | 59 | 1,0 | 58,0 | |||
| 3 | 12.03.2007 | 3,2 | 1,0 | 2,2 | |||
| 4 | 01.04.2007 | 32 | 1,0 | 31,0 | |||
| 5 | 21.04.2007 | 18 | 1,0 | 17,0 | |||
| 6 | 11.05.2007 | 6,5 | 1,0 | 5,5 | |||
| 7 | 31.05.2007 | 36 | 1,0 | 35,0 | |||
| 8 | 20.06.2007 | 100 | 1,0 | 99,0 | |||
| 9 | 10.07.2007 | 16,5 | 1,0 | 15,5 | |||
| 10 | 30.07.2007 | 2,8 | 1,0 | 1,8 | |||
| 11 | 19.08.2007 | 30 | 1,0 | 29,0 | |||
| 12 | 08.09.2007 | 2,2 | 1,0 | 1,2 | |||
| 297,0 | ← ∑ | ||||||
| A | B | C | D | E | F | G | H |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Для розробки та побудови даної математичної моделі було взято 12 періодів, t – середина інтервалів, A f = 0,2визначено графічним методом з графіків спектральної щільності, в стовбець A – занесена формула (2.2) з посиланням на коефіцієнти A, B, C, D, E, F, G, H.
Визначимо вищевказані коефіцієнти в MS Excel (табл. 3.3.). Вже перші розрахунки за допомогою функції “Пошук рішень” електронних таблиць Excel показали, що константи E та G в (2.2) визначаються як нулі у випадку, коли амплітуда синусоїди менше середнього значення функції у 3-10 разів. Тому, для збільшення точності розрахунку, рекомендується встановлювати обмеження на значення констант за наступним правилом:
На графіку, який було побудовано за статистичними даними, виділяється елемент кривої, що нагадує синусоїду і знаходиться проміжок значень агрументу, на якому ця синусоїда здійснює повне коливання – Δх. Тоді, для константи E треба встановити наступне обмеження
E ≤ (0,5 – 1,5) 2π/Δх1. (3.1)
Початкові значення констант B та F рекомендується становити рівними одиниці, константи Н – середньому арифметичному статистичного значення функції, константу – D - 0.05, А=0.
Константа C визначається з максимальної амплітуди Δу тієї частини графіку, яка визначена як синусоїдальна, і має наступні обмеження
С ≤ (0,4 – 0,6) Δу. (3.2)
Таблиця 3.3.
Математична модель з відомими коефіцієнтами
| № періоду | t | A f = 0,2 | A | ∆ = (A f = 0,2 - A)2 | |
| 1 | 31.01.2007 | 2,8 | 421,4 | 175207,1 | |
| 2 | 20.02.2007 | 59 | 39,2 | 390,3842 | |
| 3 | 12.03.2007 | 3,2 | 49,0 | 2101,777 | |
| 4 | 01.04.2007 | 32 | 31,4 | 0,362309 | |
| 5 | 21.04.2007 | 18 | 29,2 | 125,9568 | |
| 6 | 11.05.2007 | 6,5 | 27,6 | 443,4496 | |
| 7 | 31.05.2007 | 36 | 26,2 | 95,55286 | |
| 8 | 20.06.2007 | 100 | 25,1 | 5606,694 | |
| 9 | 10.07.2007 | 16,5 | 24,2 | 59,10535 | |
| 10 | 30.07.2007 | 2,8 | 34,4 | 1001,264 | |
| 11 | 19.08.2007 | 30 | 22,7 | 53,64417 | |
| 12 | 08.09.2007 | 2,2 | 25,1 | 525,4244 | |
| 1856,7 | ← ∑ |
| A | B | C | D | E | F | G | H |
| 49,04514 | -0,32172 | 435,263 | -259,325 | 18,33648 | 0,5 | 7,779768 | 10 |
Тепер, коли відомі всі коефіцієнти і систематизована модель (2.2) можливо прогнозувати направлення крос-курсів конвертованих валют в майбутньому. Прогнозування тренду крос-курсу виконується наступним чином:
в формулу (2.2) підставляеться наступний проміжок часу, період, якиий повинен бути одинаковим по розміру з попередніми;
провести обчислення (2.2) з заздалегідь відомими коефіцієнтами.
Достовірним сигналом, що в наступному періоді тренд стане зростаючий буде (табл. 3.4.):
A t ≤ At + 1 (3.3)
Достовірним сигналом, що в наступному періоді тренд стане спадаючий буде:
A t ≥ At + 1 (3.4)
Таблиця 3.4.
Прогнозування тренду в майбутньому періоді
| № періоду | t | A f = 0,2 | A | ∆ = (A f = 0,2 - A)2 | |||
| 1 | 31.01.2007 | 2,8 | 421,4 | 175207,1 | |||
| 2 | 20.02.2007 | 59 | 39,2 | 390,3842 | |||
| 3 | 12.03.2007 | 3,2 | 49,0 | 2101,777 | |||
| 4 | 01.04.2007 | 32 | 31,4 | 0,362309 | |||
| 5 | 21.04.2007 | 18 | 29,2 | 125,9568 | |||
| 6 | 11.05.2007 | 6,5 | 27,6 | 443,4496 | |||
| 7 | 31.05.2007 | 36 | 26,2 | 95,55286 | |||
| 8 | 20.06.2007 | 100 | 25,1 | 5606,694 | |||
| 9 | 10.07.2007 | 16,5 | 24,2 | 59,10535 | |||
| 10 | 30.07.2007 | 2,8 | 34,4 | 1001,264 | |||
| 11 | 19.08.2007 | 30 | 22,7 | 53,64417 | |||
| 12 | 08.09.2007 | 2,2 | 25,1 | 525,4244 | |||
| 28.09.2007 | 29,2 | 1856,7 | ← ∑ | ||||
| A | B | C | D | E | F | G | H |
| 49,04514 | -0,32172 | 435,263 | -259,325 | 18,33648 | 0,5 | 7,779768 | 10 |
Як видно з табл. 3.4. прогнозування можливо проводити до безкінечності, однак для більш ефективного прогнозування, тобто, для збільшення довірчої ймовірності, - треба в кінці кожного періоду проводити перерахунки.
0 комментариев