С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом

4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.

Рассчитаем коэффициент эластичности для линейной модели:

·                   Для уравнения прямой: y = 5,777+7,122∙x

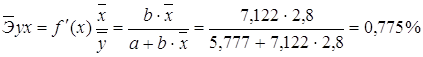
·                   Для уравнения степенной модели :

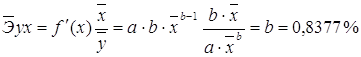
·                   Для уравнения экспоненциальной модели:

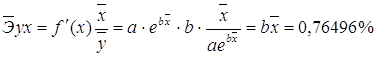
Для уравнения полулогарифмической модели :

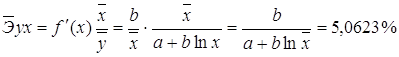
·                   Для уравнения обратной гиперболической модели :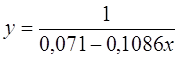

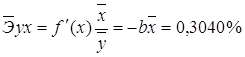
·                   Для уравнения равносторонней гиперболической модели :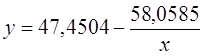

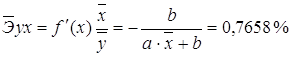
Сравнивая значения , характеризуем оценку силы связи фактора с результатом:

·                  

·                  

·                  

·                  

·                  

·                  

Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.

5. Оценка качества уравнений с помощью средней ошибки аппроксимации.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :

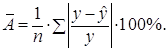
В среднем расчетные значения отклоняются от фактических на:

·                   Линейная регрессия.  = *100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

·                   Степенная регрессия. =*100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

·                   Экспоненциальная регрессия. =*100%= 9%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

·                   Полулогарифмическая регрессия. =*100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

·                   Гиперболическая регрессия. =*100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

·                   Обратная регрессия. =*100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

6. Рассчитаем F-критерий:

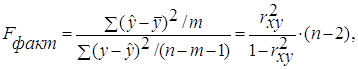
·                   Линейная регрессия. = 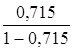*19= 47,579

где =4,38<

·                   Степенная регрессия.  =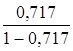*19= 48,257

где =4,38<

 

·                   Экспоненциальная регрессия. =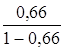*19= 36,878

где =4,38<

 

·                   Полулогарифмическая регрессия. =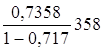*19= 52,9232

где =4,38<

·                   Гиперболическая регрессия.  =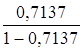*19= 47,357

где =4,38<

 

·                   Обратная регрессия. =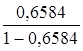*19= 36,627

где =4,38<

Для всех регрессий =4,38< , из чего следует, что уравнения регрессии статистически значимы.

Вывод:  остается на допустимом уровне для всех уравнений регрессий.

	А	R^2	Fфакт
Линейная модель	8,5	0,714	47,500
Степенная модель	8,2	0,718	48,250
Полулогарифмическая модель	7,9	0,736	52,920
Экспоненциальная модель	9,0	0,660	36,870
Равносторонняя гипербола	9,3	0,714	47,350
Обратная гипербола	9,9	0,453	15,700

Все уравнения регрессии достаточно хорошо описывают исходные данные. Некоторое предпочтение можно отдать полулогарифмической функции, для которой значение R^2 наибольшее, а ошибка аппроксимации – наименьшая

7. Рассчитаем прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определим доверительный интервал прогноза для уровня значимости α=0,05:

Прогнозное значение  определяется путем подстановки в уравнение регрессии  соответствующего (прогнозного) значения .
 5,777+7,122*2,996=27,114

где = =2,8*1,07=2,996

Средняя стандартная ошибка прогноза :

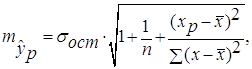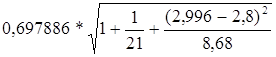==3,12

где 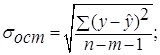= =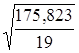0,697886

Предельная ошибка прогноза:

Доверительный интервал прогноза

 где

=27,116,53;

27,11–6,53 = 20,58

27,11+6,53 = 33,64

Выполненный прогноз среднедушевых денежных доходов в месяц, x оказался надежным (р = 1 – α = 1 – 0,05 = 0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала  составляет 2,09 раза:

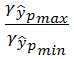= = =1,63