Навигация
Метод найменших квадратів
28744
знака
5
таблиц
10
изображений
2. Метод найменших квадратів
Модель парної лінійної регресії є власне кажучи лінійною апроксимацією (наближенням) реальної лінії регресії у(х) як умовного математичного чекання випадкового показника Y. Специфікація моделі може бути записана як: 
Тут передбачається, що α і β - точні значення параметрів моделі; хі - відомі вибіркові значення фактора; εі - випадкові помилки моделі в і-й точці з імовірностними властивостями генеральної сукупності. Очевидно, випадкові значення показника yі при цих умовах мають той же розподіл, що і помилки εі (зі зсувом 
). Для спрощення запису ми позначаємо параметри моделі β0=α, β1=β.
Оскільки на практиці замість генеральної сукупності приходиться мати справу з вибіркою обмеженого обсягу п, вдається одержати засноване на вибіркових даних наближення: yi=a+bxi+ei; i=1,2,…,n
де параметри а і b моделі є лише деякими оцінками точних значень параметрів α і β. Теоретична залежність (ТЗ) двомірної МЛР (чи апроксимуюча функція f(X, β)) описується рівнянням прямої лінії: у = а+ bх.
Тут множник b називається коефіцієнтом регресії, а величина а - постійної складової лінії регресії.
Коефіцієнт регресії 
характеризує збільшення показника при збільшенні фактора на 1 (dx = 1) і має відповідну розмірність. При зміні постійна складової а пряма коллинеарно переміщається, а її розмірність збігається з розмірністю у. Пряма лінія у = а+ bх повинна проходити так, щоб стосовно точок вибірки обсягу п 
забезпечити мінімальну середньоквадратичну помилку (СКП). Метод визначення параметрів моделі з мінімальної СКП називається методом найменших квадратів (МНК чи LSM- Least Squares Method в англомовній літературі).
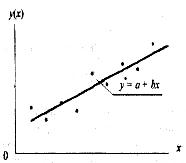
Безліч точок вибірки 
на графіку рис. 1 у декартовых координатах х,у називають діаграмою розсіювання.
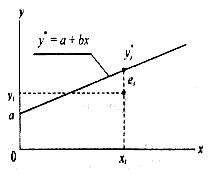
Для кожної крапки вибірки помилка результату вибірки (залишок регресії) дорівнює еі = уі - уі* = уі – а - bі
Ця помилка для і-й точки представлена на рис. 2.
|
|
|
|
Рис. 2.
Середній квадрат помилок апроксимації пропорційний сумі квадратів помилок: 
Цю згортку називають функціоналом помилок. Визначимо оцінки а і b параметрів моделі за допомогою методу найменших квадратів (МНК). Його суть складається в мінімізації функціонала помилок при варіаціях параметрів моделі. Тому що а і b поки невідомі, замінимо їх перемінними а→α і b→β. Варіації перемінних α і β дозволять знайти оптимальні за заданим критерієм оцінки.
Функціонал помилок як функція α і β має вид:
У тривимірному просторі з координатами підстави α і β ця функція являє собою поверхню з параболічними перетинами, мал. 3. Абсолютний мінімум параболічної функції при варіації лепеха має місце в точці нульових часток похідних. Для точки абсолютного мінімуму функції 
одержимо систему двох лінійних відносно α і β рівнянь:
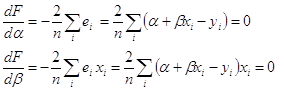
Рішення цієї системи лінійних відносно α і β рівнянь дає оцінки МНК а і b значень параметрів моделі. На мал. 3 вони показані як проекції крапки мінімуму функцій F(a, b) на координатні осі а і b підстави. Ці оцінки можуть тим більше відрізнятися від точних значень а і b в специфікації моделі, чим менше обсяг вибірки п у порівнянні обсягом генеральної сукупності N. Абсолютна точність оцінок досягається в граничному випадку (п→N, при цьому а→α і b→β). Відзначимо, що за умовами аналізу специфікації моделі а і b - фіксовані параметри, але у функції ми їх розглядаємо варїруємими перемінними для перебування оптимальних вибіркових оцінок а і b.
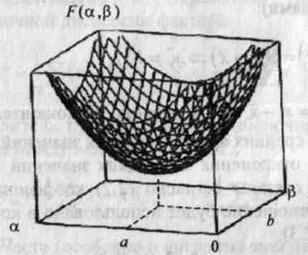
Рис. 3
З попереднього рівняння , зокрема , випливає, що сумарна помилка апроксимації (сума залишків регресії)
Крім того, це рівняння дає співвідношення між вибірковими середніми арифметичними значеннями фактора X і показника у
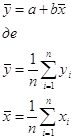
Звідси ясно, що теоретична залежність ТЗ моделі лінійної регресії у = а+ bх, побудована згідно МНК, проходить через точку середніх значень (х,у).
Рішення системи рівнянь щодо α і β має вид:
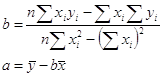
Для різних вибірок параметри а і b можуть приймати різні значення, що концентруються поблизу точних значень α і β . Тому при статистичному аналізі оцінки параметрів a і b розглядаються як випадкові величини При цьому обмовляється, за яким критерієм оптимізації отримана дана оцінка. Ми, як відзначалося, користаємося оцінками МНК із найменшим значенням функціонала помилок.
Наочне представлення вирішеної задачі побудови моделі парної лінійної регресії дає графік моделі на тілі діаграми розсіювання.
Похожие работы
... ї базується на існуванні залежності між оцінками параметрів моделі та коефіцієнтами парної кореляції. Ця залежність пропорційна до відношення середньоквадратичних відхилень залежної та незалежної змінних. 12. Опишемо алгоритм пошагової регресії. Крок 1. Усі вхідні дані стандартизують: де y* - нормалізована залежна змінна; х* - нормалізовані незалежні змінні. Крок 2. Знаходять кореляційну ...
... інших факторів на зміну результуючого показника зростає і тому робимо висновок про додаткове включення факторів в модель.) 3. Стандартні відхилення асиметрії (0,534638749) і ексцесу (0,885475609) за абсолютною величиною менші нормативного значення 1,5 і тому дають можливість судити про нормальний закон розподілу результуючого показника товарообігу. (Якщо хоча б один із цих параметрів виявиться ...
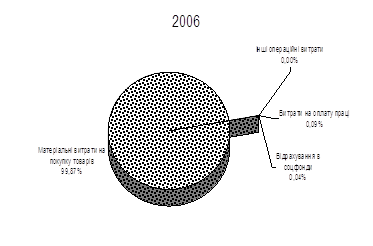
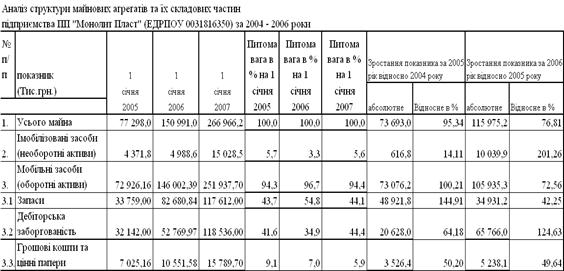
... рма не має ліцензій на торгівлю за готівку і касових апаратів. 2.2 Аналіз ефективності комерційної діяльності ПП «Монолит Пласт» по оптовому збуту сантехнічної продукції будівельним компаніям та в роздрібну торгівлю Аналіз ефективності комерційної діяльності підприємства оцінюється в процесі економічної діагностики фінансово-економічного стану підприємства і керування його фінансами, яка ...
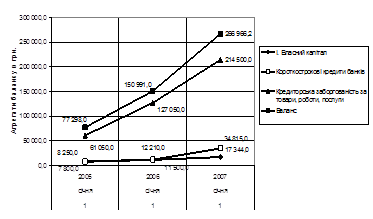
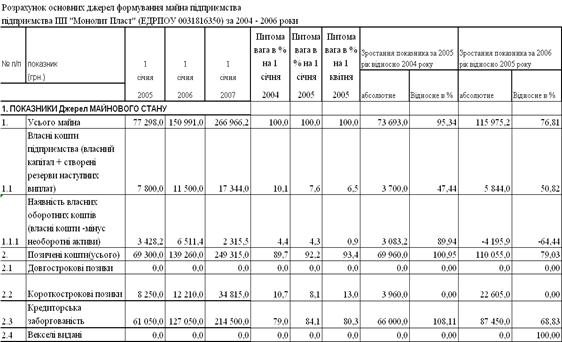
... , що зафіксовано у раніше вказаному факті використання у 2004 - 2006 році грошової маси на закупівлю товарних запасів. Оскільки на підприємстві ПП "Монолит Пласт" відсутній фінансовий відділ, а всією діяльністю підприємства управляв в 2004 – 2006 роках директор, він же головний бухгалтер за сумісництвом, увага була сконцентрована на менеджменті, характерному для приватних підприємств – хаотичний ...
0 комментариев