Навигация
Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования разностей
3.2. Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования разностей
По первоначальным динамическим рядам xi, yi с количеством членов n строим новые динамические ряды ui, wi с количеством членов n-1(табл.3.2.1), где:
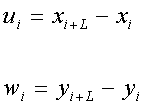 |
Таблица 3.2.1
| ui | wi |
| 640 | 224 |
| 336 | -164 |
| 164 | -276 |
| -144 | -530 |
| -316 | -410 |
| -530 | -396 |
| -450 | -44 |
| -396 | 104 |
| -84 | 456 |
| 104 | 470 |
| 416 | 590 |
| 470 | 336 |
| 550 | 224 |
| 336 | -164 |
| 184 | -276 |
| -164 | -530 |
| -316 | -470 |
| -530 | -336 |
| -450 | -44 |
| -316 | 104 |
| -164 | 456 |
| 104 | 470 |
| 416 | 590 |
| 470 | 366 |
Далее считаем автокорреляцию для динамических рядов u и w:
Для динамического ряда ui:
Для динамического ряда wi:
![]()
Т.к. полученные коэффициенты корреляции больше табличного, то переходим к следующему методу.
3.3.Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования остатков (отклонений от трендов)
В данном случае зависимость ищется в виде eyi=f(exi), где:
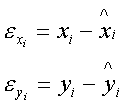 | |||
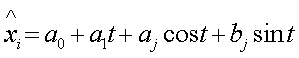 |
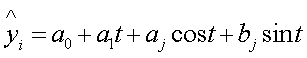 |
Значения ![]() и
и ![]() представлены в табл.3.3.1:
представлены в табл.3.3.1:
Таблица 3.3.1
3642,182105 | 5521,14579 |
| 4045,276912 | 5549,19234 |
| 4270,521342 | 5237,823029 |
| 4251,468517 | 4673,817411 |
| 3987,065165 | 4011,580844 |
| 3541,933559 | 3431,813196 |
| 3029,073401 | 3093,139015 |
| 2579,614001 | 3089,646833 |
| 2307,713526 | 3425,703505 |
| 2280,001083 | 4014,785285 |
| 2497,741411 | 4702,638546 |
| 2896,496334 | 5308,570463 |
| 3363,373599 | 5673,816955 |
| 3767,245937 | 5704,040732 |
| 3993,851263 | 5394,583544 |
| 3976,378415 | 4831,713105 |
| 3713,351191 | 4169,53091 |
| 3269,023502 | 3588,722272 |
| 2756,179857 | 3248,190391 |
| 2305,945146 | 3242,52107 |
| 2032,68507 | 3576,663941 |
| 2003,392677 | 4164,607546 |
| 2219,755627 | 4852,402924 |
| 2617,70444 | 5459,372744 |
| 3084,562645 | 5826,4751 |
![]() Для признака xi:
Для признака xi:
![]() Для признака yi:
Для признака yi:
Т.к. полученные коэффициенты корреляции опять больше табличного, то переходим к следующему методу.
Похожие работы
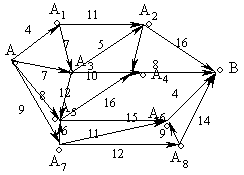
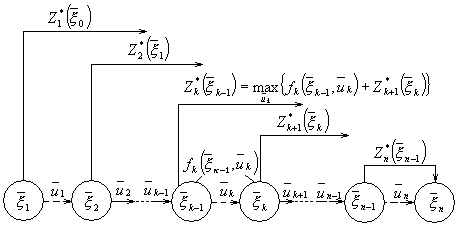
... процесс с последействием. Чтобы исключить последействие, приходится вводить несколько параметров состоянии; задача на каждом шаге остается по-прежнему сложной из-за многомерности. 2.2 Двумерная модель распределения ресурсов Задача 2. Планируется деятельность двух предприятий (s=2) в течение n лет. Начальные средства составляют . Средства x, вложенные в предприятие I, приносят к концу года ...
... 2.1. Предел статичности «черных дыр» в двоичной модели распределения плотности вещества 2.2. Горизонт «черных дыр» в двоичной модели распределения плотности вещества 3. Природа «темной материи» в двоичной модели распределения плотности вещества 4. Выводы 5. Подтверждения 6. Приложения 6.1. Фазовые переходы вещества в двоичной модели распределения плотности вещества 6.2. «Эффект темного ...
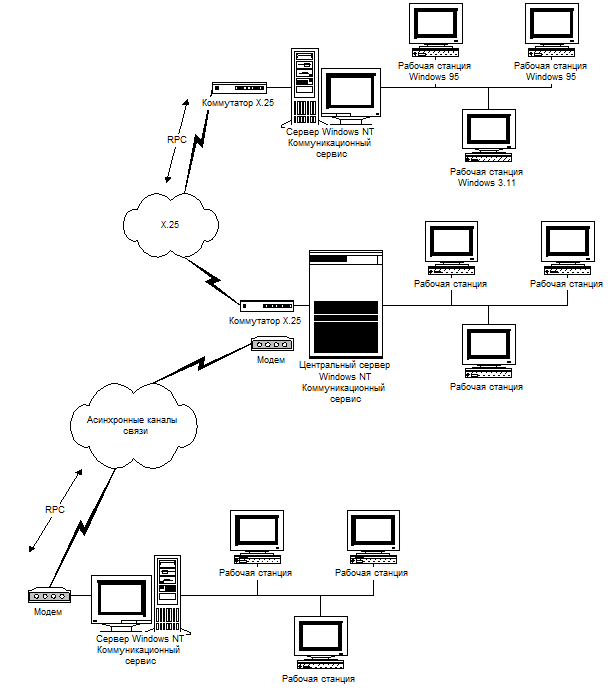
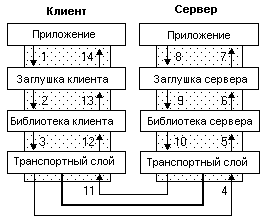
... в пенсионный фонд (1% от зарплаты) 1345 Затраты на эксплуатацию оборудования (амортизацию) 976000 ИТОГО: 1207213 Заключение За время работы над дипломным проектом по теме «Организация удаленного доступа к распределенным базам данных» были изучены теоретические основы построения распределенных информационных систем с возможностью оперативного удаленного доступа к данным. ...
... что при такой ориентации теста знания у сильных и слабых испытуемых измерялись с меньшей точностью. 3) Автоматизированный контроль знаний с применением компьютера и обработка результатов тестирования на ЭВМ для определения параметров качества тестирования. 2.1.9.4 Блок адаптивного обучения 1) Модели обучения. Информационные технологии оказывают решающее влияние на все этапы процесса обучения: ...





0 комментариев