Навигация
Режимы движения жидкости
43343
знака
28
таблиц
25
изображений
3.3 Режимы движения жидкости
Силы вязкости в жидкости существенно влияют на величину и распределение скоростей движения жидкости, т.е. на характер ее движения.
Различают два режима движения: ламинарный и турбулентный. При ламинарном режиме жидкость движется отдельными слоями, пульсаций скоростей и давлений не наблюдается. Турбулентный режим характеризуется неупорядоченным, хаотичным движением частиц и интенсивным перемешиванием жидкости.
Критерием для определения режима движения является безразмерное число Рейнольдса. Для труб круглого сечения число Рейнольдса определяется по формуле
, (3.4)
где V – средняя скорость жидкости; 
- диаметр трубы;
- кинематический коэффициент вязкости жидкости.
Экспериментально определено, что режим будет ламинарным, если 
.
- критическое число Рейнольдса, при котором происходит переход ламинарного режима в турбулентный. Для круглых труб принимают
. Если число Рейнольдса находится в области 
, то режим считается переходным, а при 
- турбулентным.
Ламинарный режим возникает в тонких капиллярных трубках, во время движения очень вязких жидкостей, при фильтрации воды в слоях грунта и др. Движение маловязких жидкостей (вода, бензин, спирт) почти всегда происходит в турбулентном режиме.
4 Гидравлические сопротивления
4.1 Общие сведения о гидравлических потерях
Движение вязкой жидкости сопровождается потерями энергии.
Потери удельной энергии (напора), или гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости.
В большинстве случаев гидравлические потери 
пропорциональны скорости течения жидкости во второй степени или динамическому напору 
и определяются из выражения
(4.1)
где 
- коэффициент потерь; V-средняя скорость в сечении.
Потери в единицах давления
. (4.2)
Гидравлические потери энергии обычно разделяют на местные потери и потери на трение по длине
. (4.3)
Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размеров русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется ее скорость и возникают вихри.
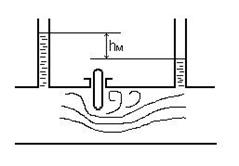
Примером местных сопротивлений может служить задвижка (рис.4.1).
|
|
| Рисунок 4.1 – Местное гидравлическое сопротивление: а) задвижка |
Местные потери напора определяются по формуле Вейсбаха
, (4.4)
где V-средняя скорость в трубе;-коэффициент местного сопротивления.
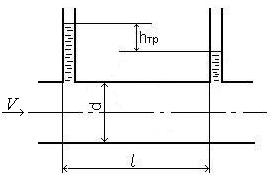
Потери на трение по длине 
-это потери энергии, которые возникают в прямых трубах постоянного сечения и возрастают прямо пропорционально длине трубы (рис.4.2).
Рассматриваемые потери обусловлены внутренним трением жидкости в трубах. Потери напора при трении определяются по формуле Дарси-Вейсбаха
, (4.5)
где λ – коэффициент гидравлического трения по длине или коэффициент Дарси; l – длина трубопровода; d –его диаметр; V – средняя скорость течения жидкости.
|
|
| Рисунок 4.2 – Потери напора по длине трубы |
Для ламинарного режима движения жидкости в круглой трубе коэффициент 
определяется по теоретической формуле
, (4.6)
где 
число Рейнольдса.
При турбулентном режиме коэффициент зависит от числа Рейнольдса Re и относительной шероховатости
(
-эквивалентная шероховатость) и определяется по эмпирическим формулам.
В области гидравлически гладких труб 4000<Re<
, т.е. при малых скоростях и числах Рейнольдса, коэффициент Дарси зависит только от числа Рейнольдса, и его определяют по формуле Блазиуса
. (4.7)
В переходной области (
) на коэффициент Дарси влияют шереховатость и число Рейнольдса. В этой области для вычислений используют формулу Альтшуля
. (4.8)
В квадратичной области сопротивления (области гидравлически шероховатых труб) коэффициент может быть найден по формуле Шифринсона
. (4.9)
Похожие работы
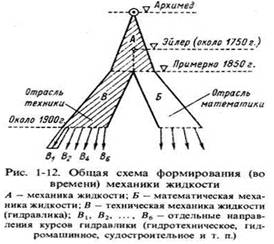
... два различных направления: "математическую механику жидкости" (см. область Б) и "техническую механику жидкости" (см. область В). Как отмечают (например, Г. Рауз и С. Инце в своей известной книге "История гидравлики"),' математическая механика жидкости зародилась еще в трудах Л. Эйлера (в середине XVIII в.). Что касается технической механики жидкости (гидравлики), то это направление механики, как ...
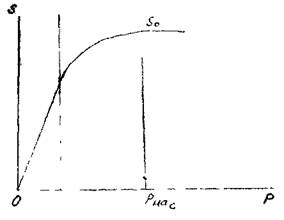
... . Для оценки режима течения жидкости вводят специальный критерий; число кавитации К f ' 7. Истечение жидкости из отверстий и насадков > 7.1. Отверстие в тонкой стенке Одной из типичных задач гидравлики, которую можно назвать задачей прикладного характера, является изучение процессов, связанных с истечением жидкости из отверстия в тонкой стенке и через насадки. ...
... собой цель детального и всестороннего описания жидких тел, что подробно рассматривается в классическом курсе физики, напомним лишь некоторые положения, которые могут пригодиться при изучении гидравлики как самостоятельной дисциплины. Так, согласно молекулярно-кинетической теории строения вещества все физические тела в природе (независимо от их размеров) находятся в постоянном взаимодействии между ...
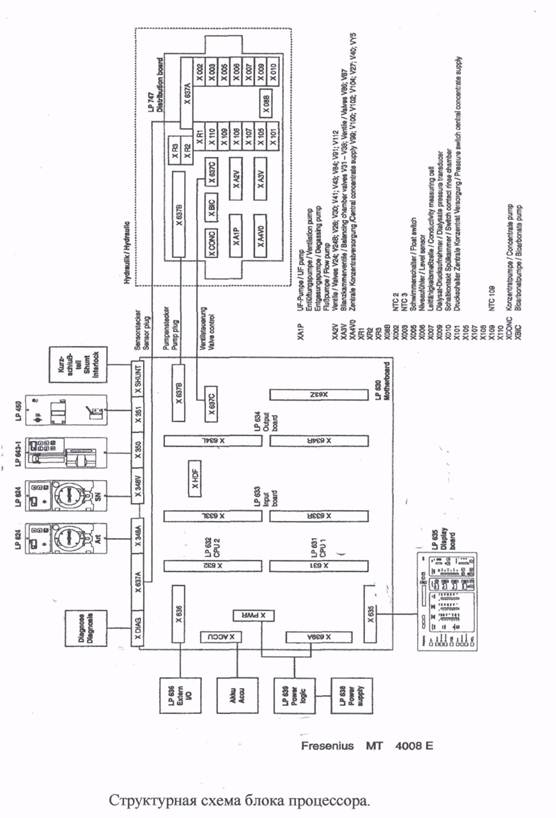
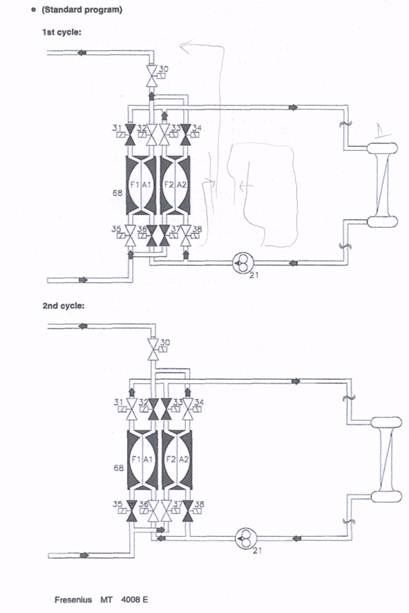
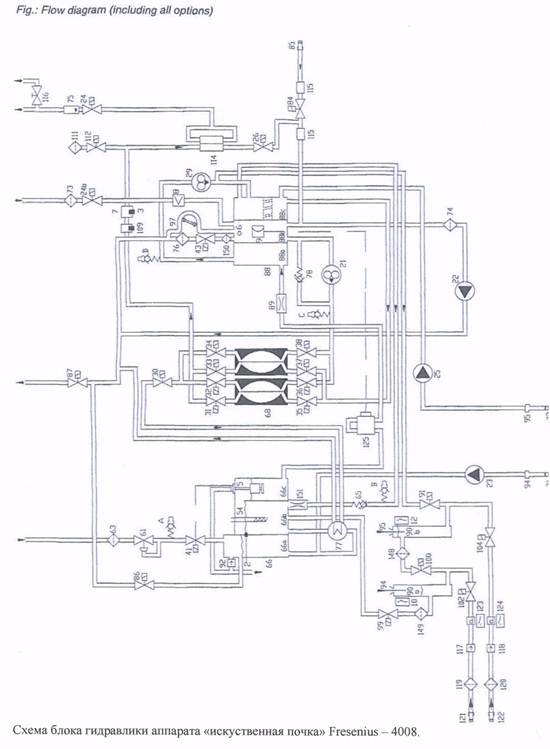
... системы смешивания концентрата - калибровка проводимости - калибровка весов гемодиафильтрации - сброс записи в памяти об ошибках - инициализация памяти NO VRAM. Перспективы развития аппарата «искусственная почка». Дальнейшее развитие аппарата «искусственная почка» связано с внедрением новых методов лечения больных. Одним из таких методов является одноигольный режим диализа (SINGLE ...
0 комментариев