Навигация
Методы математической статистики
4. Методы математической статистики.
Ìû èñïîëüçîâàëè äëÿ ðàñ÷åòà ïîëó÷åííûõ ðåçóëüòàòîâ.
Ñîáðàííûå ìàòåðèàëû ïîäâåðãëèñü ìàòåìàòè÷åñêîé îáðàáîòêå, ïðè êîòîðîé îïðåäåëÿëèñü ñëåäóþùèå ïîêàçàòåëè.
Ì – ñðåäíÿÿ àðèôìåòè÷åñêàÿ âåëè÷èíà. Îïðåäåëÿåòñÿ ñðåäíèé óðîâåíü ðàçâèòèÿ (âûðàæåííîñòè) âñåõ ïîêàçàòåëåé â îïðåäåëåííîì âàðèàöèîííîì ðÿäó:
![]() , ãäå
, ãäå
V – ïðèçíàê (âàðèàíòà),
N – êîëè÷åñòâî âàðèàíòà â âàðèàöèîííîì ðÿäó.
2.2. Îðãàíèçàöèÿ èññëåäîâàíèÿ
Èññëåäîâàíèå ïðîâîäèëîñü â íåñêîëüêî ýòàïîâ.
Íà ïåðâîì ýòàïå, ñ îêòÿáðÿ 2004 ãîäà, ïî ôåâðàëü 2005 ãîäà, èññëåäîâàëàñü ïðîáëåìà ïî ëèòåðàòóðíûì èñòî÷íèêàì, ÷òî ïîäòâåðäèëî àêòóàëüíîñòü âûáðàííîé òåìû, ïîñòàâëåíû öåëü, çàäà÷è èññëåäîâàíèÿ, îïðåäåëåíû ìåòîäû èññëåäîâàíèÿ, ñîñòàâëåí ïîíÿòèéíûé àïïàðàò, äëÿ ïîëå ïîëíîãî òåîðåòè÷åñêîãî ïîíÿòèÿ ñïåöèàëüíûõ òåðìèíîâ (ïðèëîæåíèå 1) Áûëè ïîäîáðàíû òåñòû äëÿ îïðåäåëåíèÿ ïñèõîìîòîðíûõ ñïîñîáíîñòåé. Ðàçðàáîòàíû êîìïëåêñû óïðàæíåíèé ðèòìè÷åñêîé ãèìíàñòèêè, äëÿ ñîâåðøåíñòâîâàíèÿ ïñèõîìîòîðíûõ êà÷åñòâ ñòàðøèõ øêîëüíèêîâ.
Íà âòîðîì ýòàïå èññëåäîâàíèÿ â ïåðèîä ïðîèçâîäñòâåííîé ïðàêòèêè ñî 2 ôåâðàëÿ ïî 14 ìàðòà, 2005 ãîäà ïðîâîäèëñÿ ïåäàãîãè÷åñêèé ýêñïåðèìåíò íà áàçå ëèöåÿ ¹17 ã. Ñòàâðîïîëÿ.  ñðàâíèòåëüíîì èññëåäîâàíèè ïñèõîìîòîðèêè ïðèíÿëè ó÷àñòèå äâàäöàòü øêîëüíèêîâ îò 15 äî 16 ëåò. Äåñÿòü ÷åëîâåê ñîñòàâèëè êîíòðîëüíóþ ãðóïïó è äðóãèå äåñÿòü, ýêñïåðèìåíòàëüíóþ. Îòëè÷èåì ýêñïåðèìåíòàëüíîé ãðóïïû áûëî ïðèìåíåíèå â ýòîé ãðóïïå ñðåäñòâ ðèòìè÷åñêîé ãèìíàñòèêè.
Êàê êîíòðîëüíàÿ, òàê è ýêñïåðèìåíòàëüíàÿ ãðóïïû âíà÷àëå ïðîøëè òåñòèðîâàíèå.
 ïðîöåññå ôèçêóëüòóðíûõ çàíÿòèé íàìè ïîñòåïåííî äîáàâëÿëèñü óñëîæí¸ííûå óïðàæíåíèÿ ðèòìè÷åñêîé ãèìíàñòèêè (ïðèëîæåíèå 2), ÷òî òðåáîâàëî îò çàíèìàþùèõñÿ ÷åòêîãî ñàìîêîíòðîëÿ ñâîèõ äåéñòâèé ïî âðåìåííûì, ïðîñòðàíñòâåííûì è äèíàìè÷åñêèì ïåðåìåííûì. Âñå ýòî ñïîñîáñòâîâàëî ôîðìèðîâàíèþ ó øêîëüíèêîâ òîíêèõ óìåíèé è íàâûêîâ â âîñïðèÿòèè è îöåíêå âðåìåííûõ, ïðîñòðàíñòâåííûõ è äèíàìè÷åñêèõ õàðàêòåðèñòèê äâèæåíèé.  òî æå âðåìÿ ýòî, ïîâûøàëî ó íèõ èíòåðåñ ê âûïîëíåíèþ çàäàíèé, ÷òî èìåëî âàæíîå çíà÷åíèå äëÿ ýìîöèîíàëüíîãî ôîíà óðîêà.
Ïîëó÷åííûå ðåçóëüòàòû èññëåäîâàíèÿ ìû âíåñëè â òàáëèöó (ïðèëîæåíèå 1).
ÃËÀÂÀ III. ÐÅÇÓËÜÒÀÒÛ ÈÑÑËÅÄÎÂÀÍÈß È ÈÕ ÎÁÑÓÆÄÅÍÈÅ
Ïî çàâåðøåíèþ ýêñïåðèìåíòà ìû ïîëó÷èëè êîëè÷åñòâåííûå äàííûå. Ïðè ïîìîùè ìàòåìàòè÷åñêîé îáðàáîòêè ìû âûâåëè ñðåäíþþ îöåíêó êàæäîé ãðóïïû.  íàøåì èññëåäîâàíèè âñå äàííûå ðàçäåëèëèñü íà 2 ãðóïïû: äàííûå, ïîëó÷åííûå äî ýêñïåðèìåíòà è äàííûå, ïîëó÷åííûå ïîñëå ýêñïåðèìåíòà, ÷òî ïðè ñðàâíåíèè ýòèõ äàííûõ íàì ïîçâîëÿåò íàãëÿäíî óâèäåòü ðåçóëüòàò íàøåé ðàáîòû (ïðèëîæåíèå 3). Íàïîìíèì, ÷òî â íàøåì èññëåäîâàíèè áûëî çàäåéñòâîâàíî 2 ãðóïïû ïî 10 ÷åëîâåê. Ïðè ïðîâåäåíèè Ïðîáû Ðîìáåðãà ìàêñèìàëüíûé áàëë – 5, ìèíèìàëüíûé – 0 áàëëîâ.  êîíòðîëüíîé ãðóïïå ðåçóëüòàòû óëó÷øèëèñü íà 0,5 áàëëà, â ýêñïåðèìåíòàëüíîé ãðóïïå íà 1,4 áàëëà. Òî åñòü â ýêñïåðèìåíòàëüíîé ãðóïïå ðåçóëüòàò ëó÷øå íà 0,9 áàëëà ïî ñðàâíåíèþ ñ êîíòðîëüíîé ãðóïïîé. Ýòî ïîäòâåðæäàåò íàøó ãèïîòåçó îá óñêîðåííîì ðàçâèòèè ïñèõîìîòîðíûõ ñïîñîáíîñòåé ñðåäñòâàìè ðèòìè÷åñêîé ãèìíàñòèêè (òàáëèöà 1).
Õëîïêè. Âûïîëíÿëèñü 20 õëîïêîâ ñ ìàêñèìàëüíîé ñêîðîñòüþ, 14 ñåêóíä, ñ÷èòàëñÿ õîðîøèì ðåçóëüòàòîì.
 êîíòðîëüíîé ãðóïïå ðåçóëüòàò óëó÷øèëñÿ íà 1,9 ñåêóíä, â ýêñïåðèìåíòàëüíîé ãðóïïå íà 4,3 ñåêóíäû, ÷òî ñîñòàâëÿåò ðàçíèöó â 2,4 ñåêóíäû. (òàáëèöà 1).
Ïðèñåäàíèÿ. 20 ïðèñåäàíèé âûïîëíÿëèñü ñ ìàêñèìàëüíîé ñêîðîñòüþ, õîðîøèì ðåçóëüòàòîì ñ÷èòàëîñü âûïîëíåíèå çàäàíèÿ çà 19 ñåêóíä.  êîíòðîëüíîé ãðóïïå ïðîèçîøåë ñäâèã íà 1,9 ñåê, â ýêñïåðèìåíòàëüíîé ãðóïïå íà 3,3 ñåê, ÷òî íà 1,4 ñåêóíäû ëó÷øå (òàáëèöà 1).
Íàêëîíû. Íàêëîíû âûïîëíÿëèñü ñ ìàêñèìàëüíîé ñêîðîñòüþ çà 19 ñåêóíä. Â êîíòðîëüíîé ãðóïïå ðåçóëüòàòû íà 1,1 ñåêóíäû ëó÷øå ïðåäâàðèòåëüíîãî èçìåðåíèÿ, â ýêñïåðèìåíòàëüíîé ãðóïïå íà 4,4 ñåêóíäû, ÷òî ñîñòàâëÿåò ðàçíèöó – 3,3 ñåêóíäû (òàáëèöà 1).
Òàáëèöà 1
Ñðàâíèòåëüíûå ðåçóëüòàòû íà÷àëüíîãî è êîíòðîëüíîãî òåñòèðîâàíèÿ â êîíòðîëüíîé è ýêñïåðèìåíòàëüíîé ãðóïïàõ.
| ãðóïïû | Ðîìáåðãà | Õëîïêè | Ïðèñåäàíèÿ | Íàêëîíû | ||||
| Ê | 0,5 | 0,9 | 1,9 | 2,4 | 1,9 | 1,4 | 1,1 | 3,3 |
| Ý | 1,4 | 4,3 | 3,3 | 4,4 |
Ïðè ñîñòàâëåíèè ãðóïï âíà÷àëå ýêñïåðèìåíòà ìû ñïåöèàëüíî â ýêñïåðèìåíòàëüíóþ ãðóïïó âêëþ÷èëè êàê ñèëüíûõ, òàê è áîëåå ñëàáûõ ó÷åíèêîâ. Òàêæå áûë ñäåëàí ïîäáîð è â êîíòðîëüíóþ ãðóïïó. Ïî çàâåðøåíèþ íà÷àëüíîãî
òåñòèðîâàíèÿ ñðåäíèé áàëë âî âñåõ òåñòàõ â êîíòðîëüíîé è ýêñïåðèìåíòàëüíîé ãðóïï îñîáî íå îòëè÷àëñÿ. Íåñìîòðÿ íà ýòî ïî çàâåðøåíèþ ýêñïåðèìåíòà, ñðàâíèâ íà÷àëüíûå è êîíå÷íûå ðåçóëüòàòû, ìû óâèäåëè çíà÷èòåëüíîå óâåëè÷åíèå ðåçóëüòàòà â ýêñïåðèìåíòàëüíîé ãðóïïå è íåçíà÷èòåëüíîå óâåëè÷åíèå â êîíòðîëüíîé ãðóïïå.
Óðîê ôèçè÷åñêîé êóëüòóðû â ýêñïåðèìåíòàëüíîì êëàññå â îòëè÷èå îò êîíòðîëüíîãî íà÷èíàëñÿ ñ öåëåâîé óñòàíîâêè íà âûïîëíåíèå êàæäîãî óïðàæíåíèÿ ñ ìàêñèìàëüíîé òî÷íîñòüþ. Òàê, â ïîäãîòîâèòåëüíîé ÷àñòè, âî âðåìÿ õîäüáû íà íîñêàõ, òðåáîâàëîñü ïåðåäâèæåíèå íà ïðÿìûõ íîãàõ, ñ ïîäòÿíóòûì æèâîòîì, ðàçâåðíóòûìè ïëå÷àìè, ïîäíÿòîé ãîëîâîé, áåç çàäåðæêè äûõàíèÿ. Îáðàùàëîñü âíèìàíèå íà òî÷íîå âûïîëíåíèå êàæäîãî äâèæåíèÿ. Íàïðèìåð, ïðè çàäàíèè "ðóêè íà ïîÿñ" ëîêòè äîëæíû áûòü ðàçâåðíóòû â ñòîðîíû, ïëå÷è ñëåãêà îïóùåíû, ïðè çàäàíèè "ðóêè çà ãîëîâó" êèñòè - íà çàòûëîê, îäíà íà äðóãîé, ëîêòè ìàêñèìàëüíî ðàçâåðíóòû â ñòîðîíû, ëîïàòêè ñâåäåíû è ò.ä.
Óðîêè ôèçè÷åñêîé êóëüòóðû â ýêñïåðèìåíòàëüíûõ ãðóïïàõ èìåëè êîìïëåêñíûé õàðàêòåð. Îíè âêëþ÷àëè ðàçíîîáðàçíûå óïðàæíåíèÿ ðèòìè÷åñêîé ãèìíàñòèêè íà ðàçâèòèå äâèãàòåëüíî-êîîðäèíàöèîííûõ êà÷åñòâ, èãðîâûå ìîìåíòû, èñïîëüçîâàíèå îáðàçíûõ ÿðêèõ ñðàâíåíèé - âñå ýòî äàâàëî âîçìîæíîñòü ñîçäàâàòü è ïîääåðæèâàòü ïîëîæèòåëüíîå ïñèõè÷åñêîå è ýìîöèîíàëüíîå ñîñòîÿíèå çàíèìàþùèõñÿ. Êðîìå òîãî, ìåòîäèêà çàíÿòèé â ýêñïåðèìåíòàëüíûõ ãðóïïàõ âêëþ÷àëà ñèñòåìû ñïåöèàëüíûõ óïðàæíåíèé, íàïðàâëåííûõ íà ðàçâèòèå è ñîâåðøåíñòâîâàíèå òî÷íîñòè:
1 . È.ï. - î.ñ., íà 1 - ðóêè âïåðåä, íà 2 - ââåðõ, íà 3 - â ñòîðîíû, íà 4 - è.ï.
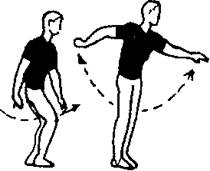
2. È.ï. - î.ñ., íà 1 - øèðîêèé âûïàä ïðàâîé âïåðåä, ïðàâóþ ðóêó â ñòîðîíó, ëåâóþ - çà ãîëîâó, ñìîòðåòü âïðàâî, íà 2 - è.ï., íà 3 - 4 - òî æå ñ äðóãîé íîãè.

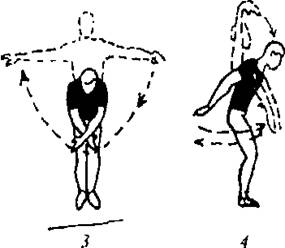
3. È.ï. - óïîð ïðèñåâ, íà 1 - ñòîéêà íà ïðàâîé, ëåâóþ íàçàä íà íîñîê, ðóêè âïåðåä-â ñòîðîíû, ëàäîíÿìè ââåðõ, íà 2 - è.ï., íà 3 - 4 òî æå ñ äðóãîé íîãè.
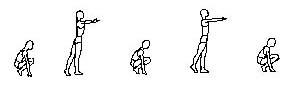
4. ×åòûðå ïðûæêà íà îäíîé íîãå, êàæäûé ñ ïîâîðîòîì íà 90O âïðàâî, çàòåì òî æå âëåâî, ðóêè íà ïîÿñ.

5. Íà 4 ñ÷åòà ïîâîðîò ïåðåñòóïàíèåì íà360O âïðàâî è íà 4 ñ÷åòà òî æå âëåâî.

6. Ïîî÷åðåäíîå ïîäáðàñûâàíèå êàæäîé ðóêîé îáðó÷à ìàíèïóëèðîâàíèå äâóìÿ îáðó÷àìè)
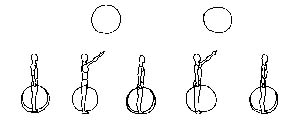
Òî÷íîñòü âûïîëíåíèÿ óïðàæíåíèé îïðåäåëÿëàñü ïî ñîîòâåòñòâèþ äâèãàòåëüíîãî äåéñòâèÿ îáðàçöîâîìó èñïîëíåíèþ. Òàê, â 1-ì è 2-ì òåñòàõ îöåíèâàëàñü òî÷íîñòü êàæäîãî äâèæåíèÿ: íàïðèìåð, â ïîëîæåíèè ðóêè âïåðåä îíè äîëæíû áûòü íà óðîâíå è øèðèíå ïëå÷, ëàäîíÿìè âíóòðü, ïàëüöû âìåñòå; òóëîâèùå ïðÿìîå, õîðîøàÿ îñàíêà, ïîäáîðîäîê ïðèïîäíÿò, ñìîòðåòü ïåðåä ñîáîé.
Äàííûå óïðàæíåíèÿ ïðîâîäèëèñü â ïîäãîòîâèòåëüíîé ÷àñòè óðîêà, ÷òî ñïîñîáñòâîâàëî ïîìèìî ðàçâèòèÿ ïñèõîìîòîðíûõ êà÷åñòâ òàêæå ðàçâèòèþ âíèìàíèÿ è äâèãàòåëüíîé ïàìÿòè. Âûñîêàÿ êîíöåíòðàöèÿ âíèìàíèÿ ÷åðåäîâàëàñü ñ ðàññëàáëåíèåì è îòäûõîì.
 çàêëþ÷èòåëüíîé ÷àñòè, ïðè âêëþ÷åíèè äàííûõ çàäàíèé íà êîîðäèíàöèþ, îñàíêó, âîññòàíîâëåíèå äûõàíèÿ è ïðè ïðîâåäåíèè ðàçëè÷íûõ èãð, òàêæå îöåíèâàëàñü òî÷íîñòü èñïîëíåíèÿ.
Òî÷íîñòü êàæäîãî äâèæåíèÿ îïðåäåëÿëàñü ïî ñòåïåíè åãî ñîîòâåòñòâèÿ âíåøíåé ôîðìå óïðàæíåíèÿ è óñòàíàâëèâàëàñü ïî ñëåäóþùèì ïàðàìåòðàì: íàïðàâëåíèþ äâèæåíèÿ, âåëè÷èíå àìïëèòóäû, ñëèòíîñòè âûïîëíåíèÿ, òåìïó è ëåãêîñòè äâèãàòåëüíîãî äåéñòâèÿ. Äâèãàòåëüíûå äåéñòâèÿ, òðåáóþùèå êîíöåíòðàöèè óñèëèé â ìèíèìàëüíîå âðåìÿ, áûñòðåå è ëåã÷å óñâàèâàþòñÿ ïðè äîñòàòî÷íî âûñîêîì óðîâíå ðàçâèòèÿ òî÷íîñòè.
Ó÷àùèìñÿ ýêñïåðèìåíòàëüíûõ ãðóïï äàâàëèñü òàêæå çàäàíèÿ, íàïðàâëåííûå íà îâëàäåíèå ðèòìè÷åñêèìè õàðàêòåðèñòèêàìè äâèæåíèé. Äëÿ óñâîåíèÿ ðèòìà èçó÷àåìîãî óïðàæíåíèÿ îïðåäåëÿëñÿ ãëàâíûé ìîìåíò ïðèëîæåíèÿ óñèëèé, âûäåëÿëèñü ïîäãîòîâèòåëüíûå è çàêëþ÷èòåëüíûå äåéñòâèÿ. Ýòî äàâàëî âîçìîæíîñòü óïðàâëÿòü îäíîâðåìåííî íåñêîëüêèìè äâèãàòåëüíûìè äåéñòâèÿìè, êîòîðûå âíåøíå âîñïðèíèìàþòñÿ êàê åñòåñòâåííûé ïîòîê äâèæåíèé.
Ïðè âûïîëíåíèè äâèãàòåëüíûõ äåéñòâèé â ýêñïåðèìåíòàëüíûõ ãðóïïàõ îáðàùàëîñü âíèìàíèå íà ñîáëþäåíèå ñëåäóþùèõ òðåáîâàíèé:
- ñòåïåíü èõ ñîîòâåòñòâèÿ îáðàçöîâîìó èñïîëíåíèþ;
- êîëè÷åñòâî ïîäõîäîâ äëÿ îâëàäåíèÿ òåõíèêîé óïðàæíåíèÿ;
- êîëè÷åñòâî íîâûõ äâèãàòåëüíûõ çàäàíèé ðàçëè÷íîé ñëîæíîñòè, âûïîëíåííûõ çà îïðåäåëåííûé ïåðèîä âðåìåíè.
 êîíòðîëüíîé ãðóïïå ó÷åíèêè çàíèìàëèñü ïî îáû÷íîé øêîëüíîé ïðîãðàììå îáó÷åíèÿ.
Ïîëó÷åííûå äàííûå ïîäòâåðæäàþò íàøó ãèïîòåçó î òîì, ÷òî ñðåäñòâàìè íåòðàäèöèîííûõ âèäîâ ãèìíàñòèêè, à èìåííî ðèòìè÷åñêîé ãèìíàñòèêè ðàçâèòèå ïñèõîìîòîðíûõ ñïîñîáíîñòåé ïðîèñõîäèò óñïåøíåå.
ÂÛÂÎÄÛ
1. Ðåçóëüòàòû òåîðåòè÷åñêîãî èññëåäîâàíèÿ ïîêàçàëè, ÷òî ïðîáëåìà ïñèõîìîòîðèêè àêòóàëüíà. Ïñèõîìîòîðíàÿ ïîäãîòîâêà ÿâëÿåòñÿ îäíîé èç îñíîâíûõ íàïðàâëåíèé â ðàçâèòèè ïñèõîìîòîðíûõ ôóíêöèé îðãàíèçìà.  ðàçâèòèè ïñèõîìîòîðíûõ êà÷åñòâ ñòàðøèõ øêîëüíèêîâ áîëüøóþ ðîëü èãðàþò ñëîæíîêîîðäèíàöèîííûå óïðàæíåíèÿ, êàêèìè è ÿâëÿþòñÿ óïðàæíåíèÿ ðèòìè÷åñêîé ãèìíàñòèêè.
2. Ýôôåêòèâíîñòü âëèÿíèÿ íåòðàäèöèîííûõ âèäîâ ãèìíàñòèêè íà ðàçâèòèå ïñèõîìîòîðíûõ êà÷åñòâ ñòàðøèõ øêîëüíèêîâ äîêàçàíî ýêñïåðèìåíòàëüíî. Ïî ïðîáå Ðîìáåðãà â ýêñïåðèìåíòàëüíîé ãðóïïå ïðîèçîøëî èçìåíåíèå íà 0,9 ñåêóíäû â îòëè÷èè îò êîíòðîëüíîé, ïî òåñòó «Õëîïêè», ðåçóëüòàò â ýêñïåðèìåíòàëüíîé ãðóïïå ëó÷øå íà 2,4 ñåêóíäû, ïî òåñòó «Ïðèñåäàíèÿ» íà 1,4 ñåêóíäû è òåñòó «Íàêëîíû» - íà 3,3 ñåêóíäû.
3.  êîíå÷íîì ðåçóëüòàòå ìû ìîæåì ñäåëàòü âûâîä, ÷òî â ýêñïåðèìåíòàëüíîé ãðóïïå, ãäå ñèñòåìàòè÷åñêè ïðèìåíÿëèñü óïðàæíåíèÿ ðèòìè÷åñêîé ãèìíàñòèêè ïîêàçàòåëè ïñèõîìîòîðíûõ êà÷åñòâ îêàçàëèñü íàìíîãî âûøå.
ËÈÒÅÐÀÒÓÐÀ
1. Àíàíüåâ Á.Ã. Ïñèõîëîãèÿ ÷óâñòâåííîãî ïîçíàíèÿ. Ì., 1960
2. Бершнтейн Н.А. Очерки по физиологии движений и физиологии активности.- М.: Медицина, 1966.
3. Бальсевич В.К. Онтокинезиология человека. - М.: 2000. - 275 с., ил.
4. Áûëååâà Ë.Â. Ïîäâèæíûå èãðû. – Ì.: «Ôèçè÷åñêàÿ êóëüòóðà è ñïîðò», 1974.
5. Годик М.А., Бальсевич В.К., Тимошкин В.Н. Система общеевропейских тестов для оценки физического состояния человека // Теор. и практ. физ. культ., 1994, № 11-12, с. 24-32.
6. Ãåëëåð Ì.Å. Ïñèõîìîòîðèêà. //Òåîð. è ïðàêò.ôèçè÷åñêîé êóëüòóðû.1984, ¹ 2.
Похожие работы
... . Гимнастки старших разрядов упражнение без предмета не выполняют. Помимо многоборья программой соревнований предусматриваются и групповые (5 гимнасток) упражнения с одним или двумя предметами. 1.2. ОСОБЕННОСТИ МЕТОДИКИ РАЗВИТИЯ ГИБКОСТИ И КООРДИНАЦИИ ДВИЖЕНИЙ, ВОЗРАСТНЫЕ ОСОБЕННОСТИ. Одним из важнейших физических качеств в художественной гимнастике является гибкость - способность выполнять ...
... 7 12 6. Подготовка и участие в соревнованиях 3 3 6 7. Приемные и переводные испытания 1 2 3 Итого: 51 89 140 8. Учебно-тематический план 2-го года обучения Спортивно-оздоровительный этап младший школьный возраст № п/п Перечень разделов Количество часов теория практика всего 1. Теоретическая подготовка 12 - 12 2. Общая физическая подготовка 16 ...
... II. Цель, задачи, методы и организация исследования 2.1 Цель и задачи исследования Цель исследования - совершенствование физической подготовленности школьников V-VI классов на физкультурных занятий групп продленного дня путем использования скоростно-силовых упражнений. Это предусматривает разработку эффективной методики развития основных физических качеств и повышения общей физической ...
... развития должны иметь право выбрать свой путь: принимать участие в жизни общества, либо предпочесть защищенность и уединение. 1.5 Коррекционная направленность воспитания и обучения детей с задержкой психического развития Вся деятельность специального дошкольного учреждения базируется на соблюдении основополагающих принципов и подходов к вопросам изучения, воспитания и обучения детей ...

0 комментариев