Погрешности

6. Погрешности

Составляющими погрешностей в данной работе являются:

·          мешающие факторы

·          моделирование

·          расчеты

·          настройка нейронных сетей

К мешающим факторам относятся: неоднородности материалов, неточное задание характеристик, неплотное прилегание датчика к объекту контроля, краевые эффекты – однако все эти факторы мы не учитываем, в силу того, что рассматриваем идеальный случай.

Погрешности моделирования складываются из неточности задания геометрии модели, шага разбиения сетки, движения дефекта (считаем, что скорость движения не превышает 0,5 м/с). Данную составляющую общей погрешности считаем не значительной, так как компьютерные средства позволяют создавать модель с высокой точностью.

В ходе получения сигналов и их обработки возникает погрешность расчетов, которая в основном обусловлена шагом, с которым мы снимаем показания. Так как этот процесс автоматизирован и рассматривается идеальная модель, эта составляющая не сильно влияет на конечный результат.

Основной составляющей погрешности является погрешность, с которой созданная нейронная сеть классифицирует дефекты и делает прогнозы. Рассмотрим ее подробнее.

Были рассмотрены три различные структуры искусственных нейронных сетей:

·          многослойный персептрон

·          вероятностная или обобщенная регрессионная нс

·          радиальная базисная функция

Стояла задача выбрать тип сети с наименьшей погрешностью на выходе.

Погрешность определения раскрытия дефекта.

Рисунок 19

На диаграмме (рис. 19) видим, что среднее значение абсолютной погрешности многослойного персептрона минимальное. И хотя все три сети удовлетворяют требованиям к определению раскрытия, преимущество у персептрона.

В табл. 3 приведены значения средней, максимальной и минимальной погрешностей посчитанных по результатам обучения всех трех сетей. Для каждой сети было использовано 100 различных значений.

error	pers	rbf	orns
average	0,054	0,061	0,063
max	0,238	0,253	0,4
min	0,001	0	0

Погрешность определения глубины дефекта.

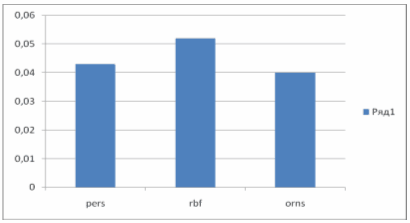
Рисунок 20

Значение среднего значения абсолютной погрешности в данном случае (рис.20) минимальна у обобщенной регрессионной нейронной сети, однако ее за основу не стоит брать. В процессе выбора архитектуры сети данного типа, сеть с наименьшей ошибкой имеет 8 входов, 62 элемента на 1 скрытом слое и 2 элемента на 2 скрытом слое. Вероятность того, что сеть с такой архитектурой при имеющемся количестве сигналов для обучения, просто запомнит сигналы, а не обучится, возрастает. Поэтому для нас предпочтительнее выбрать сеть типа персептрон.

В табл. 4 приведены значения средней, максимальной и минимальной погрешностей посчитанных по результатам обучения всех трех сетей. Для каждой сети было использовано 100 различных значений.

error	pers	rbf	orns
average	0,043	0,052	0,04
max	0,144	0,251	0,205
min	0	0,002	0

Погрешность, имеющая в данном случае интерес и максимально влияющая на результаты, является погрешностью выбранной нейронной сети. Для нас важна точность, с которой она сможет определять дефекты.

Заключение

В ходе проведенной работы была разработана, конечно элементная модель, позволяющая определять продольные и поперечные трещины. Сформирована база сигналов, по которой были рассчитаны информативные признаки, а также выявлены зависимости фазы и амплитуды от различных параметров дефекта и от нескольких частот.

С использованием информативных признаков был проведен корреляционный анализ, показавший наиболее коррелирующие признаки с параметрами дефектов. По результатам данного анализа были выбраны признаки, использованные для обучения нейронных сетей.

Полученные результаты не противоречат фундаментальным физическим законам и принципам. Погрешности лежат в допустимых пределах.

Полученные нейронные сети, могут быть использованы в дальнейших экспериментальных исследованиях по контролю продольные и поперечные дефекты труб.

Литература

1. Brudar B. How to Distinguish Surface and Subsurface Cracks // Electromagnetic NDT Methods: NDT International, Vol. 17, August 1984, p 221-223.

2. Brudar B. Magnetic Leakage Fields Calculated by the Method of Finite Differences// Electromagnetic NDT Methods: NDT International, Vol. 18, No.6, December 1985, p 353-357.

3. В.И. Егоров. Применение ЭВМ для решения задач теплопроводности. Санкт-Петербург, 2006.

4. С.Н. Бозиев. MATLAB 2006a в примерах. РГУ нефти и газа им. И.М. Губкина, 2006.

5. Song S-J. Model-based interpretation of experimental eddy current signals obtained from steam generator tubes by bobbin probe. // Insight. 2003. №5.

Приложение 1

Программа, написанная в среде MatLab для создания базы сигналов.

% параметры геометрии объекта контроля и катушек

air1H=10e-3; %толщина слоя воздуха над ОК

L=50e-3; %длинна трубы

air2H=6.5e-3; %толщина слоя воздуха под ОК

OKH=1.5e-3; %толщина трубы

OKD=8e-3; %внешний диаметр трубы

H_k=2e-3; %высота катушки

l_k=3e-3; %ширина катушки

delta_k=1e-3; %зазор между ОК и катушками

D_k = 3e-3; %расстояние между катушками

delta_izm=0.5e-3; %зазор между ОК и измерительной катушкой

r=0.01; %радиус вторичной катушки для расчетов

%Параметры геометрии дефекта по умолчанию

ld_def=1e-3; %длинна дефекта

x_def=(L/2)-ld_def; %положение центра дефекта по длине ОК

hd_def=1e-3; %глубина дефекта

fd_def=1; %форма - отношение меньшего основания к большему

 %fd = 1 - прямоугольник,

 %1<fd<0.01 - трапеция

 %fd<0.001 -> треугольник

%Параметры эксперимента

x_start=20e-3; %начало зоны контроля

x_end=0e-3; %конец зоны контроля

x_step=-0.5e-3; %шаг съема данных

hd_start=0.4e-3; %начальная глубина дефекта

hd_end=1.2e-3; %конечная глубина дефекта

hd_step=0.2e-3; %шаг по глубине

ld_start=0.1e-3; %начальная протяженность дефекта

ld_end=1.0e-3; %конечная протяженность дефекта

ld_step=0.2e-3; %шаг по ротяженности

fd=[1,0.01,0.3,0.7]; %формы

f=[25e3,100e3,200e3,400e3]; %частоты, в герцах

f_ind=1;

x_size=size((x_start:x_step:x_end)');

x_size=x_size(1);

 

clear data

 

%figure;GEOMPLOT(fem);

% скрипт эксперимента

clear data

data_ind=1;

 

for fd_ind = 1:size(fd')

for ld = ld_start:ld_step:ld_end

for hd = hd_start:hd_step:hd_end

for f_ind = 1:size(f')

 data(data_ind,1)=data_ind;

 data(data_ind,2)=fd(fd_ind);

 data(data_ind,3)=ld;

 data(data_ind,4)=hd;

 data(data_ind,5)=f(f_ind);

 x_ind=1

for x = x_start:x_step:x_end

flclear fem

 % Application mode 1

clear appl

appl.mode.class = 'AzimuthalCurrents';

appl.mode.type = 'axi';

appl.module = 'ACDC';

appl.assignsuffix = '_emqa';

clear prop

prop.analysis='transient';

appl.prop = prop;

clear pnt

pnt.I0 = {};

pnt.name = {};

pnt.ind = [];

appl.pnt = pnt;

clear bnd

bnd.chsrcdst = {};

bnd.murbnd = {};

bnd.sigmabnd = {};

bnd.eta = {};

bnd.d = {};

bnd.index = {};

bnd.Esphi = {};

bnd.pertype = {};

bnd.type = {};

bnd.A0phi = {};

bnd.name = {};

bnd.H0 = {};

bnd.Js0phi = {};

bnd.epsilonrbnd = {};

bnd.murext = {};

bnd.ind = [];

appl.bnd = bnd;

clear equ

equ.Vloop = {};

equ.Sd = {};

equ.magconstrel = {};

equ.srcpnt = {};

equ.M = {};

equ.S0 = {};

equ.Pphi = {};

equ.gporder = {};

equ.coordOn = {};

equ.sigma = {};

equ.name = {};

equ.epsilonr = {};

equ.rOn = {};

equ.dr = {};

equ.cporder = {};

equ.mur = {};

equ.normfH = {};

equ.Br = {};

equ.init = {};

equ.Stype = {};

equ.Drphi = {};

equ.R0 = {};

equ.elconstrel = {};

equ.fH = {};

equ.v = {};

equ.Jephi = {};

equ.usage = {};

equ.srcaxis = {};

equ.user = {};

equ.ind = [];

appl.equ = equ;

fem.appl{1} = appl;

fem.sdim = {'r','z'};

fem.frame = {'ref'};

fem.border = 1;

clear units;

units.basesystem = 'SI';

fem.units = units;

 

air1 = rect2(air1H,L,'base','center', 'pos', [air1H/2+OKD 0]);

OK = rect2(OKH,L,'base','center','pos', [-(OKH/2)+OKD 0]);

air2 = rect2(air2H,L, 'base','center','pos', [-(OKH+air2H/2)+OKD 0]);

kat1 = rect2(H_k,l_k, 'base','center','pos', [delta_k+(H_k/2)+OKD -((D_k/2)+(l_k/2))]);

kat2 = rect2(H_k,l_k, 'base','center','pos', [delta_k+(H_k/2)+OKD ((D_k/2)+(l_k/2))]);

 

p1=point2(OKD+delta_izm,0);

 

defect = geomcoerce('solid',{curve2([0+OKD-OKH 0+OKD-OKH],[x-(ld/2) x+(ld/2)]),...

 curve2([0+OKD-OKH hd+OKD-OKH],[x+(ld/2) x+(ld*fd(fd_ind)/2)]),...

 curve2([hd+OKD-OKH hd+OKD-OKH],[x+(ld*fd(fd_ind)/2) x-(ld*fd(fd_ind)/2)]),...

 curve2([hd+OKD-OKH 0+OKD-OKH],[x-(ld*fd(fd_ind)/2) x-(ld/2)])});

 

clear s p

 

p.objs={p1};

p.name={'p1'};

 

 

s.objs={air1,air2,OK,kat1,kat2,defect};

s.name={'air1','air2','OK','kat1','kat2','defect'};

 

draw=struct('s',s,'p',p);

 

fem.geom = geomcsg(draw);

 

fem.mesh=meshinit(fem,...

 'hmax',0.5e-3,...

 'hmaxvtx',[11,0.05e-3],...

 'hmaxedg',[4,0.2e-3,6,0.0001,7,0.0001,8,0.2e-3,9,0.0001,11,0.0001,12,0.2e-3,15,0.0001,16,0.0001,17,0.0001,18,0.0001,19,0.0001,20,0.0001,21,0.0001,22,0.0001],...

 'hmaxsub',[2,0.2e-3]);

 

% Application mode 1

clear appl

appl.mode.class = 'AzimuthalCurrents';

appl.mode.type = 'axi';

appl.dim = {'Aphi','redAphi'};

appl.sdim = {'x','z','y'};

appl.module = 'ACDC';

appl.sshape = 2;

appl.assignsuffix = '_emqa';

clear prop

prop.analysis='harmonic';

appl.prop = prop;

clear bnd

bnd.type = {'A0','cont','ax'};

bnd.ind = [3,1,1,2,1,2,2,2,2,1,2,2,1,1,2,2,2,2,2,2,2,2,1];

appl.bnd = bnd;

clear equ

equ.sigma = {0,2e6,0,0};

equ.Jephi = {0,0,1e6,1e6};

equ.ind = [1,2,1,1,3,4];

appl.equ = equ;

appl.var = {'nu',f(f_ind)};

fem.appl{1} = appl;

fem.border = 1;

 

% Multiphysics

fem=multiphysics(fem);

 

% Extend mesh

 fem.xmesh=meshextend(fem);

 

% Solve problem

 fem.sol=femstatic(fem,...

 'solcomp',{'Aphi'},...

 'outcomp',{'Aphi'},...

 'blocksize','auto',...

 'ntol',1e-012);

 

 % Integrate

 data(data_ind,5+x_ind)=-postint(fem,'Br_emqa',...

 'unit','T',...

 'recover','off',...

 'dl',11,...

 'edim',0)*i*2*pi*data(data_ind,5)*pi*r^2;

 data(data_ind,5+(2*x_size)-x_ind)=-data(data_ind,5+x_ind);

 x_ind=x_ind+1;

end

data_ind

end

end

end

end

Приложение 2

Программа, написанная в среде MatLab для расчета информативных признаков по сформированной базе сигналов.

function [y] = prizn (P)

 

for k=1:5

 for w=1:100

 y(k,w)=P(k,w);

 end;

end;

% k-ctro4ki

% w-ctolbci

 

for k=6:46

 for w=1:100

 Z(k,w)=P(k,w);

 end;

end;

 

for w=1:100

 

for k=6:46

 g(k)=Z(k,w);

end;

 

rez=real(g);

imz=imag(g);

rez=abs(rez);

imz=abs(imz);

 

mre=max(rez); %mre - max resistanse

for k=6:46

 if mre==rez(k)

 mr=k; %mr - max resistance index

 k=46;

 end

end

 

maxres=g(mr); %maxres - max resistance point (F1)

mrea=angle(maxres);

mrea=(180/pi)*mrea; %mrea - max resistance angle (F2)

 

y(6,w)=mre;

y(7,w)=mrea;

 

mim=max(imz); %max reactance

for k=6:46

 if mim==imz(k)

 mi=k; %mi - max reactance index

 k=46;

 end

end

 

maxreact=g(mi); %maxreact - max reactance point (F3)

mima=angle(maxreact);

mima=(180/pi)*mima; %mima - max reactance angle (F4)

 

y(8,w)=mim;

y(9,w)=mima;

 

absz=abs(g);

maxz=max(absz); %mabs - max impedance

for k=6:46

 if maxz==absz(k)

 mz=k; %mz - max impedance index

 k=46;

 end

end

 

maximp=g(mz); %maximp - max impedance point (F5)

mimpa=angle(maximp);

mimpa=(180/pi)*mimpa; %mimpa - max impedance angle (F6)

 

y(10,w)=maxz;

y(11,w)=mimpa;

 

stang=angle(g(6));

stang=(180/pi)*stang; %stang - starting angle (F7)

endang=angle(g(46));

endang=(180/pi)*endang; %endang - ending angle (F8)

 

y(12,w)=stang;

y(13,w)=endang;

 

c=sqrt( ( (real(g(mz))-real(g(mz-1)) )^2) +((imag(g(mz))-imag(g(mz-1)))^2));

b=sqrt(((real(g(mz+1))-real(g(mz)))^2)+((imag(g(mz+1))-imag(g(mz)))^2));

a=sqrt(((real(g(mz+1))-real(g(mz-1)))^2)+((imag(g(mz+1))-imag(g(mz-1)))^2));

 

turnang=acos(((b^2)+(c^2)-(a^2))/(2*b*c));

turnang=(180/pi)*turnang;

 % turnang - turning fase angle at the point of max impedance (F9)

 

y(14,w)=turnang;

 

L(1)=sqrt( ((real(g(6)))^2) +((imag(g(6)))^2));

for k=7:46

 L(k)=sqrt( ( (real(g(k))-real(g(k-1)) )^2) +((imag(g(k))-imag(g(k-1)))^2));

end

L(47)=sqrt( ( (real(g(46)))^2) +((imag(g(46)))^2));

for k=1:mr

 L1(k)=L(k);

end

mrlen=sum(L1); %mrlen - length up to the max resistance point (F10)

totlen=sum(L); %totlen - total length (F11)

 

y(15,w)=mrlen;

y(16,w)=totlen;

 

end;