Навигация
Енергія електрона в кристалі залежить від компонент хвильового вектора k. Вона є парною функцією хвильового вектора k, тобто
8. Енергія електрона в кристалі залежить від компонент хвильового вектора k. Вона є парною функцією хвильового вектора k, тобто
E(k)=E(-k).
9. При дії на кристал температури і тиску, що приводять до зміни відстані між атомами, буде змінюватися область перекриття хвильових функцій і, отже, величина обмінного інтеграла. Це викличе зміну ширини енергетичних зон, в результаті зміниться і ширина забороненої зони між цими зонами.
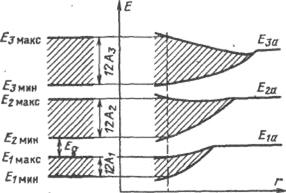
Рис.3.1. Утворення зон енергії з енергетичних рівнів при зближенні атомів, а – постійна гратки кристала.
10. Метод сильного зв'язку непридатний до зовнішніх валентних, електронам атомів кристалів, оскільки із-за великого перекриття хвильових функцій сусідніх атомів ширина енергетичної зони валентних електронів приблизно дорівнює відстані між рівнями енергії в ізольованому атомі або перевищує їх.
Розділ 4. Зони Бріллюена
При
зміні хвильового вектора від 0 до π/а енергія електрона
зростає неперервно, при ![]() виникає перший розрив. Дала енергія знов зростає неперервно, але при
виникає перший розрив. Дала енергія знов зростає неперервно, але при ![]() знов виникає наступний
розрив.
знов виникає наступний
розрив.
Області
значень хвильового вектора ![]() при
якому енергія електрона змінюється неперервно називають зонами
Бріллюєна.
при
якому енергія електрона змінюється неперервно називають зонами
Бріллюєна.
В енергетичній зоні кристала є N енергетичних станів, яким відповідають значення компонент хвильового вектора:
![]() (4.1)
(4.1)
і компонент квазіімпульсу
![]() (4.2)
(4.2)
Де i=x, y, z, а j = 1, 2, 3.
Значенням квазіімпульсу в системі координат (рх, ру, рz) відповідатиме деяка область, побудована навколо початку координат і що містить всі можливі різноманітні стани. Ця область називається першою, або основною, зоною Брілюєна. Для кристала з простий кубічною граткою перша зона Брілюєна є кубом (рис. 4.1, а) об'ємом:
![]() (4.3)
(4.3)
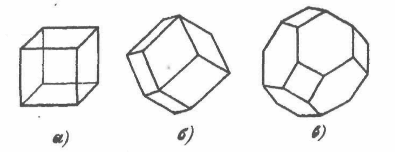
Рис. 4.1 Перша зона Брілюєна для кристала з простою кубічною решіткою (а), кубічною об’ємноцентрованою (б), кубічною гранецентрованою решітками (в).
Оскільки об'єм першої зони Бріллюена для кристала з простими кубічними гратками дорівнює (h/а)3, а об'єм елементарної комірки h3/a3N, то число елементарних комірок в ній складає N, тобто рівне кількості енергетичних станів в зоні. Але в енергетичній зоні може розташовуватися 2N електронів, отже, і в першій зоні Брілюєна може бути 2N електронів, а в її кожній комірці може знаходитися тільки два електрони з протилежно направленими спінами.
Друга і наступні зони Бріллюена, які відповідають відповідно другій і наступним енергетичним зонам, мають складнішу конфігурацію, але їх об'єм залишається постійним. Вони також містять N елементарних комірок, кожну з яких можна надати у відповідність комірку в першій зоні, що описує еквівалентний стан.
4.2. Приведені зониОперація побудови всіх енергетичних зон в межах першої зони, називається приведенням зон до першої зони, а самі зони, побудовані таким чином, називаються приведеними зонами. Приведення зон полягає в зсуві по осі енергій ділянок кривої E(k), що відносяться до різних зон, на відрізки, кратні 2π/а. На рис. 4.4 пунктиром показана 2-а, 3-а і частково 4-а приведені зони, горизонтальними стрілками – напрям зсуву при побудови цих зон, в розривах стрілок вказана величина зсуву. З рисунка видно, що у всіх непарних приведених зон в центрі розташовуються мінімуми, а на межах зон максимуми; у парних зон, навпаки, в центрі розташовуються максимуми, на межах – мінімуми.
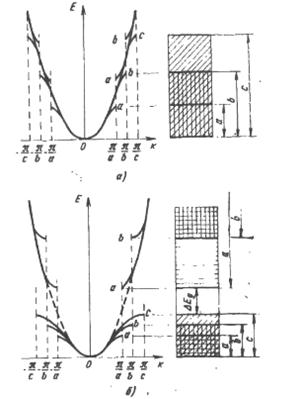
Мал. 4.4. Перекриття енергетичних зон.
а) дозволені зони накладаються на заборонені; б) заборонені зони для різних напрямків кристалів накладаються одна на одну, утворюючи абсолютно заборонену зону для кристала в цілому.
Аналогічним чином будуються приведені зони для тривимірних кристалів. Оскільки періодичність решіток в тривимірному кристалі у різних напрямах може бути різною, то значення k, при яких настає бреггівське відбиття і виникають розриви в енергетичному спектрі електрона, будуть також різними: для напряму, уздовж якого періодичність решітки рівна а, розриви настають при ![]() , для напряму з періодичністю b – при
, для напряму з періодичністю b – при ![]() , для напряму з періодичністю с – при
, для напряму з періодичністю с – при ![]() і так далі. Внаслідок цього область енергій, заборонена для певних напрямів, може перекриватися областями дозволених енергій для інших напрямів (рис. 4.4,а) і енергетичний спектр в цілому виявиться безперервним. Тільки у тому випадку, коли області заборонених енергій для всіх напрямів накладаються один на одного (рис. 4.4,б), в кристалі існуватимуть абсолютно заборонені області енергій і його енергетичний спектр збереже зонний характер.
і так далі. Внаслідок цього область енергій, заборонена для певних напрямів, може перекриватися областями дозволених енергій для інших напрямів (рис. 4.4,а) і енергетичний спектр в цілому виявиться безперервним. Тільки у тому випадку, коли області заборонених енергій для всіх напрямів накладаються один на одного (рис. 4.4,б), в кристалі існуватимуть абсолютно заборонені області енергій і його енергетичний спектр збереже зонний характер.
Розглянемо рух електрона в кристалі під дією зовнішнього поля напруженості Е. Поле діє на електрон із силою F = eE. У випадку цілком вільного електрона ця сила є єдиною. На електрон, який перебуває в кристалі, крім неї діє періодичне поле решітки. Тому рух електрона в кристалі виявляється значно більше складним, чим рух вільного електрона в потенційному ящику. Один з способів опису цього руху полягають у наступному. Швидкість руху електрона в кристалі дорівнює груповій швидкості поширення електронних хвиль і визначається формулою i
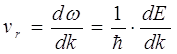 (4.10)
(4.10)
За час dt зовнішня сила F виконує роботу з переміщення електрона, чисельно рівну: ![]() (4.11)
(4.11)
Диференціюючи по часу визначимо прискорення електрона:
![]() (3.12)
(3.12)
![]() (3.13)
(3.13)
Формула (3.13) встановлює зв'язок між прискоренням електрона й зовнішньою силою, що діє на нього з боку зовнішнього електричного поля Е. Вона виражає, отже, другий закон Ньютона. Із цієї формули видно, що під дією зовнішньої сили F електрон у періодичному полі кристала рухається в середньому так, як рухався б під дією цієї сили вільний електрон, якби він мав масу:
![]() (3.14).
(3.14).
Маса ![]() називається ефективною масою електрона. Приписуючи електрону, що перебуває в періодичному полі кристала, масу
називається ефективною масою електрона. Приписуючи електрону, що перебуває в періодичному полі кристала, масу ![]() , ми можемо вважати цей електрон вільним та описувати його рух у зовнішнім полі так, як описується рух звичайного вільного електрона. До речі, для вільного електрона, для якого
, ми можемо вважати цей електрон вільним та описувати його рух у зовнішнім полі так, як описується рух звичайного вільного електрона. До речі, для вільного електрона, для якого ![]() , формула (3.14) дає:
, формула (3.14) дає: ![]() що, потрібно було очікувати.
що, потрібно було очікувати.
Необхідно підкреслити, що введення поняття ефективної маси є лише зручним способом опису поводження електрона в періодичному полі кристала. Сама ж ефективна маса не є масою у звичайному змісті слова. Вона не визначає ні гравітаційних, ні інерційних властивостей електрона. По величині вона може бути як більше, так я менше маси вільного електрона, за знаком – як позитивною, так і негативною.
4.4. Енергетична будова алмазоподібних напівпровідників.Кремній і германій мають кристалічну структуру типу алмаза, що представляє собою дві гранецентровані кубічні решітки, зміщені одна щодо іншої на 1/4 просторової діагоналі. Елементарний осередок містить два атоми. Для них перша зона Брілюєна не є кубом, а має форму чотирнадцятигранника, зображеного на рисунку 4.5, де значення складових хвильового вектора ![]() дані в одиницях 2п/а (а - ребро куба решітки).
дані в одиницях 2п/а (а - ребро куба решітки).
Розрахунок зонної структури напівпровідників являє собою складне завдання. Для германія й кремнію залежність Е (к) для довільно обраної точки к є рівнянням 146-й ступеня. Тому енергія була обчислена лише для деяких симетрично розташованих точок зони Брілюєна, для яких розрахунок сильно спрощується. Але й при цьому довелося чисельно розв’язувати рівняння 16-й степені. Дані для проміжних точок у зоні Брілюєна були отримані інтерполяцією. Результати теоретичних розрахунків уточнювалися порівнянням із даними експериментів, зокрема по циклотронному резонансу.
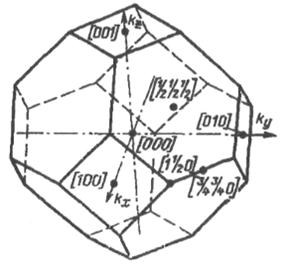
Рис. 4.5. перша зона Брілюєна для напівпровідника типу алмазу.
У атома кремнію є 14 електронів, а в атома германія – 32 електрона, які розподілені по зонах Брілюєна наступним чином:
Si1s22s22р63s23р2
Ge1s22s22р63s23р6d410S 24p2
У них остання оболонка не заповнена, у ній у р – стані є два електрони з паралельними спинами. Оскільки зона провідності й валентна зона кремнію й германія включають р - стан, для якого в кристалі виродження знімається, то кожна з них являє собою накладення трьох різних зон. На рис. 4.6 вони представлені трьома вітками Е(к). Ця залежність неоднакова для різних кристалографічних напрямків.
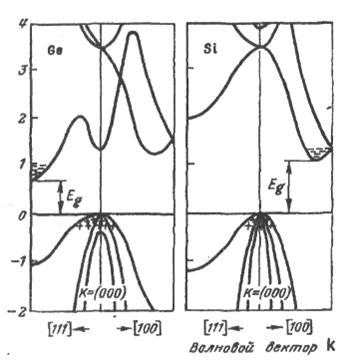
Рис. 4.6. енергетична структура германію та кремнію. Еg – ширина забороненої зони, знаком «+» зображено дірки в валентній зоні, знаком «-» електрони в зоні провідності.
Одна з галузей Е (к) зони провідності як у кремнію, так й у германію (рис. 4.6) лежить значно нижче інших. Положення абсолютного мінімуму енергії визначає дно зони провідності. Мінімуми енергії називають також долинами.
Абсолютний мінімум зони провідності в германію розташований у напрямку осей 11111 (рис. 4.6), тому є вісім еквівалентних мінімумів енергії, координати яких в одиницях 2к/а мають вигляд (1/2, 1/2, 1/2) і лежать на границі зони Бріллюєна (на рис. 4.6 вони показані жирною точкою). Ізоенергетичні поверхні поблизу абсолютних мінімумів енергії (або долин) являють собою еліпсоїди обертання відносно великої напівосі. І на першу зону Брілюєна припадає половина кожного еліпсоїда енергії, а отже, у германію є не вісім, а тільки чотири повних еліпсоїди енергії (рис. 4.7).
Абсолютний мінімум зони провідності в кремнію лежить у напрямку осей (1001) неподалік від границі зони Брілюєна (рис. 4.6). Тому в кремнію є шість еквівалентних мінімумів анергії, а отже, у кремнію на першу зону Брілюєна доводиться шість еліпсоїдних поверхонь постійної енергії, витягнутих уздовж осей 11001 (рис. 4.6). Центри еліпсоїдів розташовані на відстані трьох чвертей від центра зони Брілюєна.
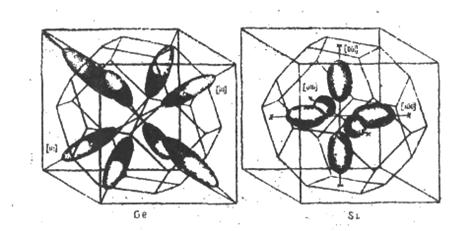
Рис. 4.7. Форми поверхонь постійної енергії в зонах провідності германію та кремнію.
Залежність енергії від хвильового вектора k до поблизу абсолютних мінімумів зони провідності в германії й кремнії виражається формулою
![]()
Мінімальна відстань між дном зони провідності й вершиною валентної зони називається шириною забороненої зони. У кремнію й германію екстремуми енергії електронів і дірок лежать у різних точках зони Брілюєна (рис. 4.7). При кімнатній температурі й нормальному атмосферному тиску ширина забороненої зони в германію достатньо високого ступеня чистоти дорівнює 0,67 еВ, у кремнію вона становить 1,11 еВ.
Розділ. 5. Заповнення зон електронами та електричні властивості напівпровідників
Кожна енергетична зона містить, як ми вияснили, обмежене число енергетичних рівнів. Відповідно до принципу Паулі на кожному рівні може розміститися не більше двох електронів. При обмеженому числі електронів, що утримуються у твердому тілі, заповненими виявляться лише декілька найбільш низьких енергетичних зон.
По характеру заповнення зон електронами всі тіла можна розділити на дві великі групи.
1. До першої групи відносять тіла, у яких над цілком заповненими зонами розташовується зона, заповнена лише частково (рис. 5.1,а). Така зона виникає в тому випадку, коли атомний рівень, з якого вона утвориться, заповнений в атомі лише частково. Типовим прикладом цьому можуть служити лужні метали. У натрію, наприклад, що має електронну конфігурацію
11Na ls2s2p63s1, на рівні 3s перебуває один електрон, у той час як для заповнення цього рівня необхідно два електрони. Тому зона 3s, що утвориться із рівня 3s, виявляється заповненою лише наполовину.
Частково заповнена зона може виникати й внаслідок накладення заповнених зон на порожні або частково заповнені зони, як це має місце в лужноземельних металів (мал. 5.1,б). Наявність зони, заповненої електронами лише частково, характерно для металів.
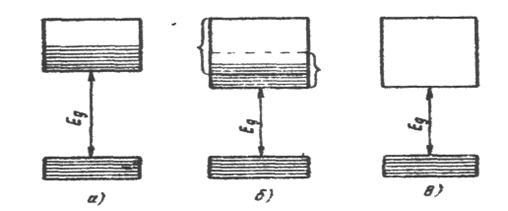
Рис. 5.1. Зонна структура твердих тіл.
2. До другої групи відносять тіла, у яких над цілком заповненими зонами розташовуються порожні зони (мал. 5.15,в). Типовим прикладом твердих тіл із таким характером заповнення зон є елементарні напівпровідники IV групи таблиці Менделєєва: алмаз, кремній, германій. Як уже вказувалося раніше, валентна зона цих елементів, що містить чотири стани на атом, заповнена чотирма валентними електронами, у той час як зона провідності, що містить також чотири стани на атом, виявляється зовсім порожньою.
До цієї ж групи твердих тіл ставляться й багато хімічних сполук. Всі вони є або напівпровідниками або діелектриками.
Відповідно до зонної теорії твердих тіл електрони зовнішніх енергетичних зон мають практично однакову свободу руху у всіх тілах, незалежно від того, є вони металами або напівпровідниками (діелектриками). У відсутності зовнішнього поля цей рух не може, однак, привести до виникнення електричного струму, тому що розподіл електронів по швидкостях є симетричним. Це означає, що якщо в кристалі вибрати електрон, що рухається з даною швидкістю в даному напрямку, то обов'язково знайдеться інший електрон, що має швидкість таку ж по величині, але протилежну по напрямку.
Розглянемо з погляду зонної структури електричні властивості, якими повинні володіти напівпровідники (діелектрики).
У напівпровідників і діелектриків зони валентних електронів (валентні зони) заповнені цілком і відділені від вільної зони досить широким енергетичним інтервалом. Зовнішнє поле, прикладене до такого кристала, не в змозі змінити характер руху електронів у валентній зоні, тому що воно не здатне підняти електрони у вільну зону, яка розташована вище. Усередині ж самої зони, що не містить жодного вільного рівня, воно може викликати лише перестановку електронів місцями, що не порушує симетрії розподілу їх по швидкостях. Тому в таких тілах електричне поле не може викликати появи спрямованого руху електронів, тобто появи електричного струму, незважаючи на наявність «вільних» електронів, здатних рухатися по всьому тілу.
Природно, що такі тіла при абсолютному нулі повинні мати нульову електропровідність, тобто бути ізоляторами. Однак з підвищенням температури, внаслідок термічного порушення електронів валентної зони, частина з них може отримати енергію, достатню для подолання забороненої зони й переходу в зону провідності. Остання перетворюється тоді в частково зайняту, а в раніше цілком заповненій валентній зоні з'являються вакансії, по яких може відбуватися рух електронів. Чим менша ширина забороненої зони й вище температура кристала, тим більше електронів переходить у вільну зону й тем більше вакансій утвориться у валентній зоні. Для тіл, у яких ширина забороненої зони не перевищує 1 еВ, уже при кімнатній температурі в зоні провідності виявляється достатнє число електронів, а у валентній зоні – вакансій, щоб обумовити відносно високу електропровідність. Такі тіла звичайно називають напівпровідниками.
Звідси стає ясним, що розподіл твердих тіл другої групи, на діелектрики й напівпровідників є чисто умовним. У міру того, як у якості напівпровідників починають використовувати матеріали з усе більше широкою забороненою зоною, подібний розподіл поступово втрачає свій сенс.
Розділ 6. Діркова провідність напівпровідників
Електрони валентної зони, у якій є вільні стани, під дією зовнішнього електричного поля можуть переходити на ці стани й створювати в кристалі електричний струм. Визначимо миттєву величину цього струму.
Миттєвий струм, створюваний одним електроном, що рухається зі швидкістю v, дорівнює:
І0 = -ev (6.1)
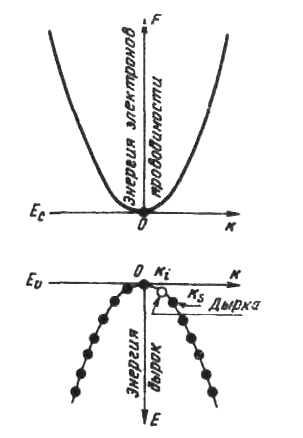
Припустимо, що таким електроном є електрон, стан якого характеризується хвильовим вектором ks (рис. 6.1).
 Результуючий миттєвий струм для всієї сукупності електронів у зоні дорівнює:
Результуючий миттєвий струм для всієї сукупності електронів у зоні дорівнює:
![]() (6.2),
(6.2),
де сумування ведеться по всіх станах, зайнятим електронами. Для зони, повністю укомплектованої електронами, І=0, тому що будь-якому електрону із хвильовим вектором ks, і швидкістю руху v, найдеться електрон із хвильовим вектором -ks, і швидкістю -vs.
Рис. 6.1. Ілюстрація до поняття
дірки у валентній зоні.
Припустимо тепер, що в зоні зайняті всі стани, крім одного, що характеризується вектором kі, і швидкістю руху vі (рис. 6.1). Сумарний струм в такій зоні буде рівний:
![]() (5.3)
(5.3)
Оскільки перша складова правої частини рівняння рівна нулю, то: ![]() (5.4), (6.4)
(5.4), (6.4)
Із виразу (5.4) видно, що сумарний струм всіх електронів у зоні, що має один вакантний стан, еквівалентний струму, утвореному однією частинкою з позитивним зарядом +е, поміщеною в цей стан. Такі фіктивні частинки називаються дірками. Фіктивними вони є тому, що в дійсності не існують. Введення їх пояснюється тим, що вони дозволяють досить складну задачу про рух величезного числа електронів валентної зони по вакантних рівнях замінити значно більш простою задачею про рух невеликого числа дірок, що розташовуються на цих рівнях.
Дірки, як й електрони, мають ефективну масу. По абсолютній величині ефективна маса дірки дорівнює ефективній масі електрона, що раніше займав даний вакантний стан. Оскільки знак заряду дірки протилежний знаку заряду електрона, то для виникнення струму дірок, еквівалентного струму, створюваного колективним рухом електронів, знак ефективної маси дірок повинен бути протилежний знаку ефективної маси електронів, що розташовуються у вершини валентної зони. Як відомо, такі електрони мають негативну ефективну масу. Тому ефективна маса дірок повинна бути позитивною.
У табл. 6.1 наведені ефективні маси електронів і дірок, визначені методом циклотронного резонансу.
Таблиця 6.1. Ефективні маси дірок та електронів.
| Тип кристала | Електрони | Дірки | ||
| Прокольна маса, mi | Поперечна маса, mt | Легкі важкі | Важкі дірки | |
| Германій | 1,58 m | 0,082 m | 0,04 m | 0,3 m |
| Кремній | 0,7 m | 0,19 m | 0,16 m | 0,5m |
| InSb | Ефективна маса ізотропна та рівна 0,014m | |||
Розділ 7. Домішкові рівні у напівпровідниках
Напівпровідники будь-якого ступеня очищення містять завжди домішкові атоми, що створюють свої власні енергетичні рівні, що одержали назву домішкових рівнів. Вони можуть розташовуватися як у дозволений так й у забороненої зонах напівпровідника на різних відстанях від вершини валентної зони й дна зони провідності. У ряді випадків домішки вводять свідомо для надання напівпровіднику потрібних властивостей.
Розглянемо основні типи домішкових рівнів.
7.1. Донорні рівніПрипустимо, що в кристалі германію частина атомів германію заміщена атомами миш’яку (арсену, As). Германій має решітку типу алмаза, кожен атом оточений чотирма атомами, пов'язаними з ним валентними силами. Для зв'язку із цими атомами атом миш'яку витрачає 4 валентних електрони (рис. 7.1).
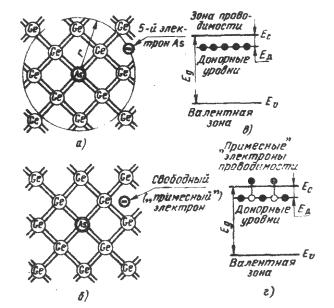
Рис. 7.1. збудження носіїв заряду в напівпровідниках n – типу.
а) при Т = 0 К атоми п’ятивалентного миш’яку в решітці германію знаходяться в неіонізованому стані,
б) «іонізація» атомів миш'яку та утворення «домішкових» електронів провідності при Т>0 К,
в) енергетичні рівні електронів миш'яку,
г) перехід електронів із донорного рівня на рівень провідності при Т > 0 К.
П'ятий електрон в утворенні зв'язку не бере участі. Він продовжує рухатися в поле атомного залишку миш’яку, ослабленому в германії в ε раз, де ε ÷16 - діелектрична постійна германію. Внаслідок такого ослаблення поля орбіта електрона сильно зростає й атом миш'яку стає подібним до атома водню: навколо атомного залишку із зарядом +е на значній відстані від нього рухається один електрон. Тому для визначення енергії зв'язку й радіуса орбіти цього електрона можна скористатися формулами, виведеними для атома водню. Вони мають вигляд:
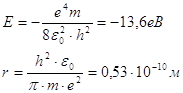 (7.1)
(7.1)
При
переході до атома миш’яку в формулах (6.1) потрібно ![]() замінити на
замінити на ![]() , оскільки сила
взаємодії електрона із ядром, яка в вакуумі рівна
, оскільки сила
взаємодії електрона із ядром, яка в вакуумі рівна ![]() , зменшується в
германії в ε разів, крім того масу вільного електрона потрібно
замінити на ефективну масу електрона в германії
, зменшується в
германії в ε разів, крім того масу вільного електрона потрібно
замінити на ефективну масу електрона в германії ![]() . Провівши такі
перетворення, одержимо:
. Провівши такі
перетворення, одержимо:
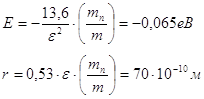 (7.2)
(7.2)
З (5.43) видно, що енергія зв'язку п'ятого електрона атома миш'яку, поміщеного в решітку германія, повинна вимірюватися приблизно сотими частками електрон-вольта, а радіус орбіти цього електрона в багато разів перевищує постійну решітки германія.
У табл. 7.1 наведені експериментальні значення енергії іонізації домішкових атомів п’ятивалентних елементів у германію й кремнію. Для германію вона дорівнює приблизно 0,01 еВ, для кремнію – приблизно 0,04÷0,05 еВ. При наданні електрону такої енергії, він відривається від атома й здобуває здатність вільно переміщатися в кристалі, перетворюючись, таким чином, в електрон провідності (мал. 7.1, б).
Таблиця 1.1. Рівні енергій донорних домішок.
|
| Фосфор | Миш’як | Стибій |
| Si | 0,045 | 0,05 | 0,039 |
| Ge | 0,012 | 0,013 | 0,01 |
З погляду зонної теорії цей процес можна представити в такий спосіб. Між заповненою валентною зоною й вільною зоною провідності розташовуються енергетичні рівні Ед п'ятого валентного електрона домішкових атомів миш'яку (рис. 7.1,в). Ці рівні розміщаються безпосередньо поблизу дна зони провідності, на відстані Ед<<0,01 еВ. При наданні електронам таких домішкових рівнів енергії Ед вони переходять у зону провідності (рис. 7.1, г). Утворені при цьому позитивні заряди локалізуються на нерухомих атомах миш'яку й в електропровідності не беруть участі.
Так як енергія збудження домішкових електронів Ед майже на два порядки нижче енергії збудження власних електронів германія Eg, то при нагріванні будуть збуджуватися в першу чергу електрони домішкових атомів, внаслідок чого їхня концентрація може в багато разів перевершувати концентрацію власних електронів напівпровідника. У цих умовах германій буде володіти в основному домішковою електронною провідністю.
Домішки, що є джерелом електронів провідності, називаються донорами, а енергетичні рівні цих домішок – донорными рівнями. Оскільки один домішковий атом припадає приблизно на 106 атомів основної речовини, то домішкові атоми практично не взаємодіють один з одним. Тому домішкові рівні не утворюють енергетичну зону і їх зображують як один локальний енергетичний рівень ЕD, на якому перебувають "зайві" електрони домішкових атомів, не зайняті в ковалентні зв’язках. Енергетичний інтервал ΔEи= Ec-ED називається енергією іонізації. Величина цієї енергії для різних п’ятивалентних домішок лежить у межах від 0,01 до 0,05 еВ, тому "зайві" електрони легко переходять у зону провідності.
7.2. Акцепторні рівніПрипустимо тепер, що в решітці германію частина атомів германію заміщена атомами тривалентного індію (рис. 7.2, а). Для утворення зв'язків із чотирма найближчими сусідами в атома індію не вистачає одного електрона.
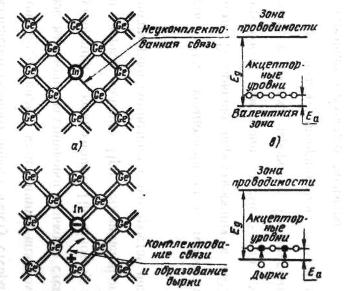
Рис. 7.2. Збудження домішкових носіїв зарядів у напівпровідниках р-типу:
а) атоми тривалентного індію в решітці германію при Т=0 К. Четвертий зв'язок атома індію не укомплектований;
б) при Т>0 К електрони можуть переходити на неукомплектовані рівні домішкових атомів, що веде до утворення іона індію й незаповненого рівня (дірки) у валентній зоні германія Еа;
в) енергетичні рівні неукомплектованих зв'язків домішкових атомів являють собою акцепторні рівні;
г) перехід електронів з валентної зони на акцепторні рівні при Т>0 К приводить до виникнення дірок.
Його можна запозичити в атома германію. У табл. 5.2 приведена енергія, необхідна для забезпечення такого «запозичення» електрона атомами бора, алюмінію, галію й індію з валентної зони германію й кремнію. З даних табл. 7.2 видно, що Еа має той же порядок величини, що й Ед.
Таблиця 7.2. Рівні енергій акцепторних домішок.
|
| Бор | Алюміній | Галій | Індій |
| Si | 0,045 | 0,06 | 0,07 | 0,16 |
| Ge | 0,010 | 0,01 | 0,011 | 0,011 |
![]() Розірваний зв'язок (мал. 7.2,б) являє собою дірку, тому що вона відповідає утворенню у валентній зоні германію вакантного місця.
Розірваний зв'язок (мал. 7.2,б) являє собою дірку, тому що вона відповідає утворенню у валентній зоні германію вакантного місця.
На рис. 7.18,б показана енергетична схема германію, що містить домішку індію. Безпосередньо у вершині валентної зони на відстані Еа розташовуються незаповнені енергетичні рівні атомів індію. Близькість цих рівнів до валентної зони приводить до того, що вже при порівняно низьких температурах електрони з валентної зони переходять на домішкові рівні. Зв'язуючись із атомами індію, вони втрачають здатність переміщуватися в решітці германію й у провідності не беруть участі. Носіями заряду є лише дірки, що виникають у валентній зоні. Тому провідність германію в цьому випадку є в основному дірковою.
Домішки, що захоплюють електрони із валентної зони напівпровідника, називаються акцепторними домішками, а енергетичні рівні цих домішок – акцепторними рівнями.
7.3. Рівні присипанняДо дрібних рівнів ставляться й так звані рівні прилипання, або, як їх іноді називають, пастки захвату. Вони також розташовуються поблизу границь енергетичних зон та активно обмінюються із даними зонами носіями зарядів. Обмін полягає в тому, що електрон зони провідності захоплений рівнем прилипання, розташованим поблизу дна даної зони, не залишається тривалий час на рівні, а внаслідок теплового збудження переходить на в зону провідності (рис. 7.3)
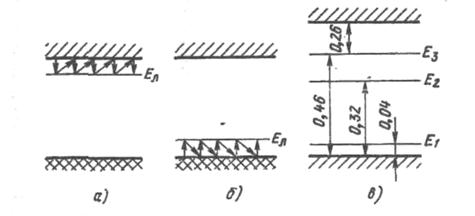
Рис. 7.3. Рівні прилипання (а, б) та глибокі домішкові рівні в напівпровіднику (в).
Аналогічний обмін між дірками відбувається між валентною зоною й рівнями прилипання, розташованими поблизу вершини цієї зони (рис. 7.3, б ). Наявність у напівпровіднику рівнів прилипання може істотно збільшити час життя нерівновагих носіїв заряду.
7.4. Глибокі домішкові рівніДеякі домішки в напівпровідниках приводять до виникнення домішкових рівнів, розташованих далеко від границі енергетичних зон. Такі рівні називаються глибокими. Як приклад на мал. 7.3 показані домішкові рівні атомів міді, введених у германій. При абсолютному нулі температури атом міді є нейтральним. З підвищенням температури він захоплює з валентної зони германію спочатку один, потім два й, нарешті, три електрони, перетворюючись у трикратно негативно заряджений іон. У валентній зоні германію утворяться при цьому три дірки. Цей процес можна розглядати й так: атом міді при Т=0оК має три дірки, які переходять у валентну зону германію с підвищенням температури. Енергії, необхідної для «відриву» від атома міді першої дірки, відповідає рівень Е1 другої дірки – рівень Е2, третьої дірки – рівень Е3. Як видно з мал. 7.3, в, рівні Е2 й Е3 є глибокими рівнями.
Крім міді, глибокі домішкові рівні в германію та кремнію дають атоми золота, марганцю, заліза, нікелю, кобальту й платини. Ці рівні відіграють значну роль у протіканні процесів рекомбінації неосновних носіїв заряду.
Висновки
Метою даної роботи було вивчення зонної структури напівпровідників.
1. У роботі було розглянуто поділ речовин на метали, діелектрики та напівпровідники, встановлено їх основні електрофізичні характеристики.
2. На основі рівняння Шредінгера встановлено зонний характер енергетичних спектрів електронів у кристалах напівпровідників. Розглянуто приблизні розв’язки рівняння Шредінгера для кристала напівпровідника.
3. Дане пояснення поняття зон Бріллюєна, та встановлена енергетична будова таких напівпровідникових матеріалів як германій та кремній.
4. На основі теорії будови напівпровідників показано введення поняття дірки, яка є певною мірою віртуальною частинкою, але введення такого поняття дозволяє складну задачу про рух величезного числа електронів валентної зони по вакантних рівнях замінити значно більш простою задачею про рух невеликого числа дірок, що розташовуються на цих рівнях.
5. У роботі розглянуто вплив домішок на структуру та електрофізичні властивості напівпровідників, утворення донорних та акцепторних рівнів, рівнів прилипання.
Список використаної літератури
1. Епифанов Г. И. Физические основы микроэлектроники. М.:
Советское радио, 1971, 374 с.
2. Шалимова К. В. Физика полупроводников. М.: Энергия, 1976, 417 с.
3. Гаман Н. И. Физика полупроводниковых приборов. Томск.
Издательство Томского университета, 1989. 335 с.
4. Случинская И. А. Основы материаловедения и технологи
полупроводников. М.: Либрус, 2002, 376 с.
5. Киттель И. Квантовая теория твёрдого тела. – М. :Мир, 1967. – 491 с.
6. Харрисон У. Теория твёрдого тела. – М. :Мир. – 1978. – 616 с.
7. Ансельм А. И. Введение в теорию полупроводников. – М.: Мир, 1965. – 588 с.
8. Бир Г.А., Пикус Г.Е. Симметрия и деформационные эффекты в полупроводниках. – М.: Наука, 1972. – 583 с.
9. Каллуей Дж. Теория энергетической зонной структуры. – М. :Мир, 1969. – 354 с.
Похожие работы
... івнює , а в домішкових напівпровідниках має зміст енергії іонізації донорів чи акцепторів. Отже, питома електропровідність напівпровідників експоненційно збільшується з ростом температури, чим останні принципово відрізняються від металів. Розділ VII. Фізика ядра та елементарних часток. § 7.1. Склад і характеристики ядра Ядро атома, як центральну позитивно заряджену масивну частину атома, ...
... параметрів при термоциклюванні, а саме ця особливість є принциповою для практичного використання. Перспективними для вирішення проблеми деградації об’ємних матеріалів з ФПМН є склокерамічні матеріали на основі компонента з фазовим переходом метал-напівпровідник. Такі матеріали можна отримати за керамічною технологією. Важливою вимогою до них, окрім стабільної поведінки при термоциклюванні, є ...
... політипів, які характеризуються також тетраедричним розміщенням атомів. Тип зв’язку в цих кристалах може змінюватися від чисто іонного характеру до ковалентного і змішаного [2]. Моделі структур сфалериту і в’юрциту показані на рис.1(а,б), параметри гратки в таблицях 1,2. Всі халькогеніди цинку і кадмію і в частковості CdTe, ZnTe і ZnSe кристалізуються в структурі цинкової обманки типу (В3). ...
... та контролю температури; германієві та кремнієві площинні діоди. Теоретичні питання знання, яких необхідне для виконання лабораторної роботи: 1. Фізичні процеси, які відбуваються в результаті контакту напівпровідників з різним типом провідності. 2. Електронно-дірковий перехід у рівноважному стані. Енергетична діаграма. 3. Інжекція та екстракція носіїв заряду. 4. Вольт амперна характеристика ( ...

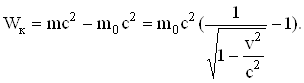



0 комментариев