Свойства металлов определяются электронами на поверхности Ферми или вблизи нее

5. Свойства металлов определяются электронами на поверхности Ферми или вблизи нее.

6. Движение волнового пакета, связанного с волновым вектором  описывается уравнением

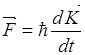
Групповая скорость

 

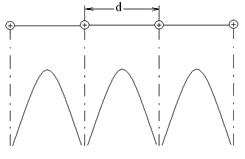
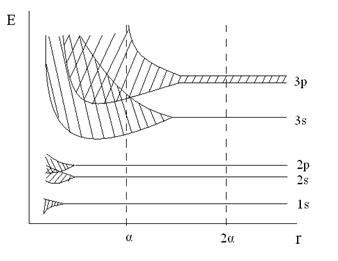
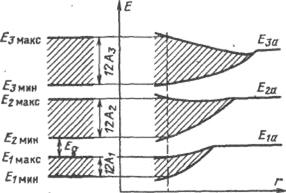
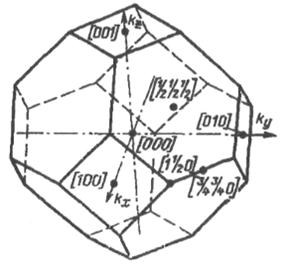
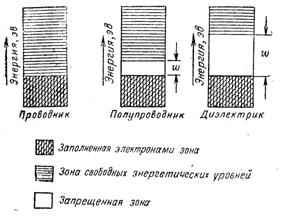
§ Энергетический спектр энергии для свободных электронов в периодическом поле

На рисунке заштрихованные области запрещенных значений энергии (энергетические щели).

Волновая функция имеет вид:

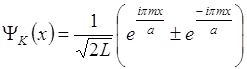
Энергия  не является теперь непрерывной функцией квазиимпульса , она непрерывна только в зонах разрешенных энергий и претерпевает разрывы на границах зон Бриллюэна. Энергетические зоны являются следствием периодической структуры кристалла и представляют собою фундаментальные характеристики электронной структуры твердого тела. – граница зоны, это вектор обратной решетки.

Области значений , при которых энергия электронов изменяется непрерывно, а на границах претерпевает разрыв, называются зонами Бриллюэна.

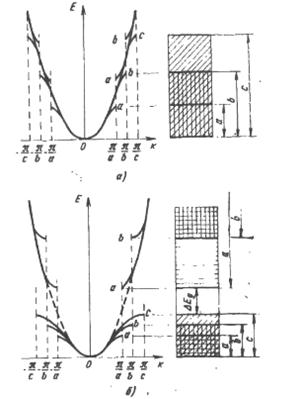
Энергетический спектр электронов и дырок в координатах Е – К. В германии и кремнии зона проводимости описывается двумя значениями масс.

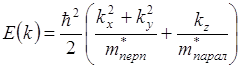
§ Механизм электропроводности собственного полупроводника

 

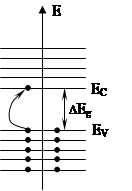
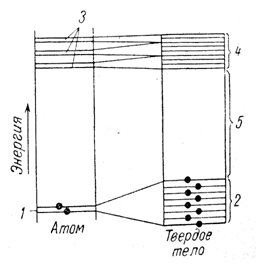
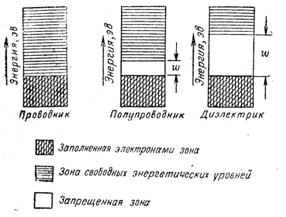
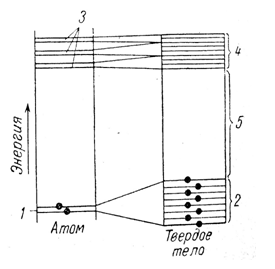
Содержащую электроны зону с наибольшей энергией, называют валентной зоной. Первую зону с незанятыми энергетическими уровнями называют зоной проводимости, так как электроны в этой зоне участвуют в переносе заряда. В проводниках валентная зона и зона проводимости либо совпадают, либо перекрываются. В изоляторах и полупроводниках эти зоны отделены друг от друга.

Если материал находится не в состоянии основном, а обладает дополнительной энергией – тепловым возбуждением. Эта энергия играет важную роль в свойствах электропроводности.

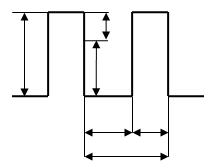
Проводник в основном состоянии, если отсутствует тепловая энергия т.е. Т = 0. Зависимость вероятности заполнения электронами энергетических уровней при КТ = 0 от энергии e отсчитывается от дна зоны.

для всех значений энергии, соответствующих заполненным уровням.

Энергия, отсчитываемая от дна зоны, при которой величина f(E) скачком изменяется от 1 до 0, называется энергией Ферми e_F В данном случае  т.е. работе выхода

При наличии тепловой энергии некоторые электроны возбудятся и перейдут из первоначальных состояний на свободные энергетические уровни. Для электронов с энергией вблизи e_F такие переходы более вероятны, так как требуется меньшая энергия возбуждения. Соответственно, и вероятность заполнения состояний уменьшается с ростом их энергии. Если электроны не подчиняются принципу Паули, то их распределение по энергии описывается классическим распределением Максвелла – Больцмана

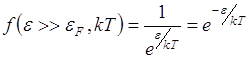Распределение, учитывающее принцип Паули, называется распределением Ферми – Дирака

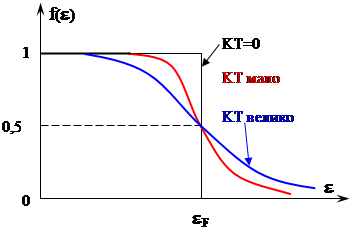
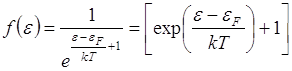
Распределение Ферми – Дирака при различных значениях КТ показано на рисунке. Здесь энергия Ферми имеет смысл энергии уровня, которому отвечает 50%-ная вероятность заполнения.

Число свободных уровней (вакансий) ниже уровня Ферми, и их распределение относительно e_F совпадает с числом и распределением заполненных состояний выше уровня Ферми. Эти состояния отвечают тепловому возбуждению электронной системы и обеспечивают появление кинетической энергии направленного движения. С ростом температуры (увеличение КТ) уменьшается наклон кривой f(e) вблизи e_F и увеличивается вероятность заполнения состояний с большими энергиями.

Из выражений для f(E, K, T) видно, что проводимость материалов сильно зависит от температуры.

В полупроводниках положение уровня Ферми соответствует формально потолку валентной зоны, но это неверно. Пусть с потолка валентной зоны (с энергией e_V) отдельный электрон от возбуждения перешел на дно (с энергией e_C) пустой зоны проводимости.

e_V – потолок валентной зоны

e_C – дно зоны проводимости.

На рисунке уровень Ферми находится в середине запрещенной зоны, учитывая симметрию распределения Ферми – Дирака относительно энергии Ферми e_F и очевидную симметрию функции f(E) в промежутке между потолком валентной зоны и дном зоны проводимости.

* Определим вероятность перехода электрона в зону проводимости для алмаза, ширина запрещенной зоны e_g»5,5 эв. при комнатной температуре КТ = 0,026 эв. для дна зоны проводимости

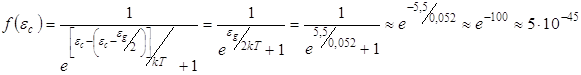
Таким образом, вряд ли даже один из каждых 10⁴⁴ электронов в валентной зоне будет иметь энергию, достаточную для перехода в зону проводимости при комнатной температуре. Поскольку каждый моль вещества содержит около 10²⁴ атомов. Следовательно, алмаз – хороший изолятор.

Определим для  вероятность при КТ = 0,026 эв. (комнатная)

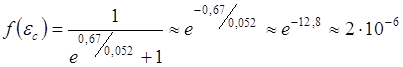
В этом случае приблизительно один валентный электрон из миллиона может при возбуждении перейти на дно зоны проводимости и в зоне проводимости можно найти электроны.

Их будет значительно меньше, чем в случае проводника, у которого f(e) в зоне проводимости составляет порядка единицы. Однако в зоне проводимости полупроводника все же имеется достаточно электронов и они вносят вклад в электропроводность полупроводника. В полупроводниках f(e) сильно зависит от температуры. Возрастание температуры на 10⁰К относительно комнатной (300⁰К) т.е. всего на 3% вероятность перехода электронов в зону проводимости увеличивается приблизительно на 30%. С уменьшением ширины запрещенной зоны чувствительность полупроводников к температуре возрастает.

Возбуждаясь с переходом в зону проводимости, электроны оставляют после себя в валентной зоне незанятые состояния или «дырки». Заполненная первоначально валентная зона становится частично заполненной и, следовательно, в ней возможны энергетические возбуждения электронов, хотя очень небольшого числа. Дырка ведет себя подобно положительно заряженной частице, которая может участвовать в электрической проводимости. Реальному движению электронов соответствует более или менее свободной фиктивное движение дырок в направлении внешнего электрического поля.

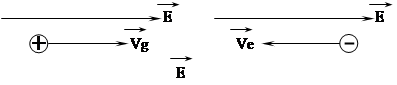
Дырки реагируют на внешнюю силу (например, на внешнее электрическое поле) не так, как свободные электроны, поэтому, чтобы учесть влияние других атомов на подвижность дырок, им приписывают эффективную массу m*, которая немного больше эффективной массы электрона.

Плотность тока электронов и дырок

где n – концентрация электронов,

р – концентрация дырок,

m_n – подвижность электронов,

m_p – подвижность дырок.

Под действием внешнего электрического поля электроны и дырки приобретают скорости направленного движения, дрейфовые скорости

m_nи m_др - подвижности

Для собственных полупроводников n=p

или

где , s - коэффициент

n – сильно зависит от температуры в зоне проводимости, в то время как подвижности слабо зависят от температуры

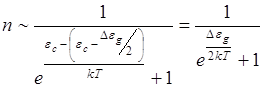
Если концентрация электронов в зоне проводимости мала, то вероятность заполнения каждого уровня мала по сравнению с единицей в знаменателе, то ею можно пренебречь.

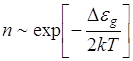 и следовательно , или

Электропроводность собственных полупроводников возрастает с температурой, у проводников уменьшается.

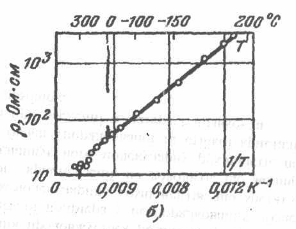
Если прологарифмировать 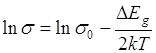и построить график зависимости lns от , то получим прямую линию, угловой коэффициент которого равен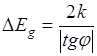

Это дает возможность, измеряя электропроводность полупроводника при различных температурах, определить опытным путем ширину запрещенной зоны  для данного полупроводника

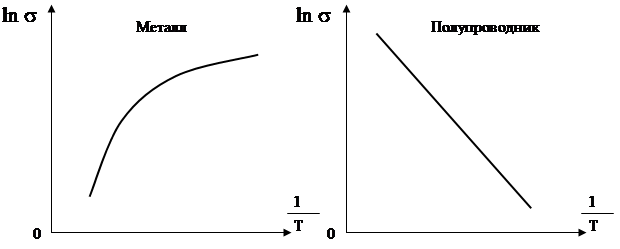
Для металлов с ростом температуры сопротивление увеличивается

R₀ –сопротивление при t = 0⁰С

R_t – сопротивление при t⁰С

a – термический коэффициент сопротивления, равный 1/273

Для металлов

Для полупроводников сопротивление с ростом температуры быстро уменьшается или  где КВ=Е_a, то

где E_a – энергия активизации, она различна для разных интервалов температур.

Наличие энергии активации E_a означает, что для увеличения проводимости к полупроводниковому веществу необходимо подвести энергию. Полупроводники – это вещества, проводимость которых сильно зависит от внешних условий: температуры, давления, внешних полей, облучения ядерными частицами.

Полупроводники – это вещества, имеющие при комнатной температуре удельную электрическую проводимость в интервале от 10^-8 до 10⁶ Сим м^-1, которая зависит сильно от вида и количества примеси, и структуры вещества, и от внешних условий.

* В полупроводнике с собственной проводимостью число электронов равно числу дырок, каждый электрон создает единственную дырку.

Число возбужденных собственных носителей экспоненциально зависит от 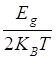, где Е_g – ширина энергетической запрещенной зоны.

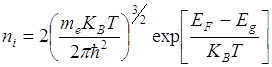
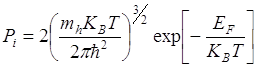
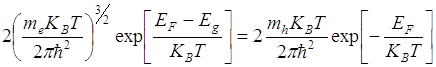
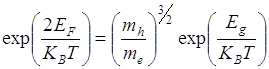
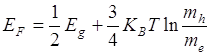
Если m_C=m_h, то 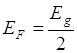т.е. уровень Ферми лежит в середине запрещенной зоны.

Индекс I (intrinsic – собственность)

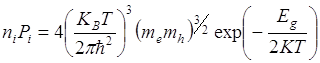
Не содержит уровня Ферми.

Это закон действующих масс, который утверждает, что расстояние уровня Ферми от краев обеих зон должно быть велико по сравнению с КТ = 0,026 эв. При 300⁰К (комнатная температура), при условии m_e = m_h = m, произведение n_iP_i

для германия 3,6 × 10²⁷ см^-6,

для кремния 4,6 × 1019 см^-6.

Энергия активации E_a для собственного полупроводника равна половине ширины запрещенной зоны

Примесные полупроводники

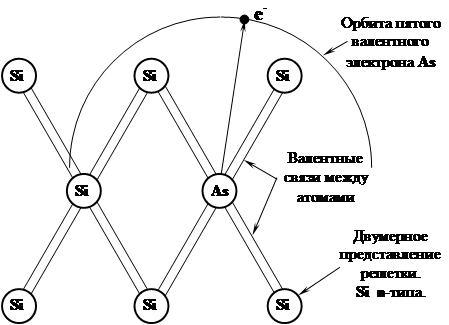
Расположение зарядов в решетке кремния. Четыре электрона A_s образуют тетраэдрические ковалентные связи, подобные связям Si, а пятый электрон A_sосуществляет проводимость. Мышьяк (As) имеет пять валентных электронов, а кремний (Si) – только четыре. Атом мышьяка называется донором, он отдает при ионизации электрон в зону проводимости.

Добавка примеси к полупроводнику называется легированием.

E_d = 0,020 эв., энергия ионизации

При К_ВТ<< E_d (низкая концентрация электронов проводимости)

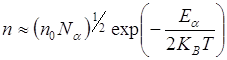где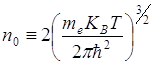

N_d - концентрация доноров

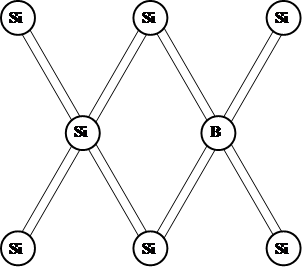
Если в кремний ввести атом бора (В), который имеет три валентных электрона, он может «укомплектовать» свои тетраэдрические связи, лишь заимствовав один электрон из связи Si – Si, образуя дырку в валентной зоне кремния, которая принимает участие в проводимости. Атом бора называется акцептором именно потому, что при ионизации захватывает электрон из валентной зоны.

Примеси, не способные к ионизации, не влияют на концентрацию носителей и могут присутствовать и в больших количествах – электрические измерения не обнаруживают их.

N_a – концентрация акцепторов.

Условием применимости классической статистики является неравенство

, откуда E_F<E_C-KT, т.е. полупроводник является невырожденным (подчиняется классической статистике), если уровень Ферми лежит ниже зоны проводимости не менее, чем на КТ.

Если уровень Ферми лежит выше Е_с более чем на 5КТ, то полупроводник полностью вырожденный. Условие вырождения зависит от температуры и положения уровня Ферми относительно дна зоны проводимости.

Концентрация электронов в невырожденном полупроводнике: F < E_c–KT,

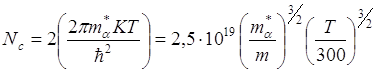
N_c – число состояний в зоне проводимости

Вырожденный полупроводник

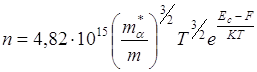
F>E_C+5KT

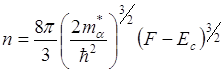она не зависит от температуры.

Уровень Ферми находится в зоне проводимости выше ее дна не менее чем на 5 КТ.

В невырожденном полупроводнике концентрация дырок определяется статистикой Больцмана при условии F > E_v + KT т.е. уровень Ферми лежит выше потолка валентной зоны на величину КТ.

В полностью вырожденном полупроводнике  или F<E_v-KT

т.е. в валентной зоне ниже ее потолка на величину не менее 5КТ. N_v – число состояний в валентной зоне.

Невырожденный полупроводник

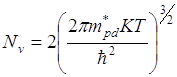
Вырожденный полцпроводник

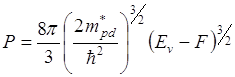
В невырожденном:

не зависит от уровня Ферми

В вырожденном

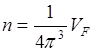где V_F – объем зоны Бриллюэна. Для сферических поверхностей , 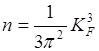где радиус сферы Ферми

Функция распределения электронов:

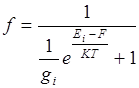
где g_i – степень вырождения, если E_i=E_d принадлежит донорной примеси, то g_i=2. Если E_i=E_a принадлежит акцепторной примеси, то g_i=1/2

Распределение электронов по донорным уровням

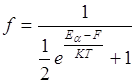
по акцепторным

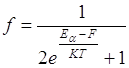
Для дырок:

;

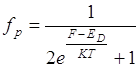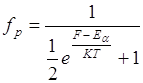
Число электронов:

 

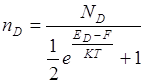
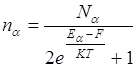
Число дырок:

 

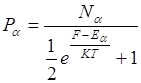
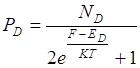
N_D = N_a = 0 собственный полупроводник.

Уравнение электронейтральности n = P. Если N_v = N_c т.е. , тогда откуда положение уровня Ферми от температуры не зависит и лежит посередине запрещенной зоны. Собственный полупроводник является невырожденным.

Генерация электронов и дырок проводимости в собственном полупроводнике:

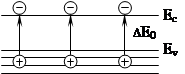
Переход каждого электрона из валентной зоны порождает в ней дырку.

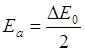
Если N_V ¹ N_C, то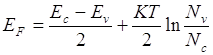

Уровень Ферми при Т = 0, лежит в середине запрещенной зоны, он линейно зависит от температуры.

Температурная зависимость уровня Ферми в собственном полупроводнике. С ростом температуры уровень Ферми приближается к той зоне, которая имеет меньшую плотность состояний и поэтому заполняется быстрее.

или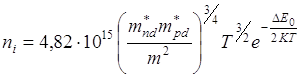

На рисунке график ln n_i от обратной температуры представляет прямую линию:

Зависимостью ln1/T по сравнению с линейным членом можно пренебречь. Угол наклона прямой определяется шириной запретной зоны:  откуда  tg s измеряется по графику (ln n_i, 1/T)

Оценим собственную концентрацию носителей заряда в германии и кремнии 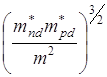 равны 0,299 и 0,719, и при Т»300⁰К,

и

Концентрация носителей заряда при Т ® 0 обращается в нуль, и сопротивление собственного полупроводника должно расти до бесконечности. Однако, в реальных полупроводниках всегда остается примесь, которая обеспечивает проводимость при любых температурах.

Тепловая генерация на рисунке носителей заряда в полупроводнике с донорной примесью.

Низкие температуры: электроны проводимости определяются концентрацией примеси, которая возникает за счет ионизации донорной примеси.

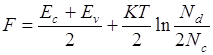
При повышении температуры уровень Ферми повышается, проходит при некоторой температуре через максимум, затем опускается. При K_d=N_2C он снова находится в середине между Е_С и Е_D.

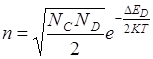
При достаточно высокой температуре N_C >> N_D, то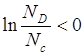

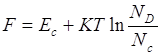
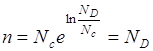
концентрация электронов не зависит от температуры и равна концентрации примеси. (Область истощения примеси). Носители заряда называют основными, если их концентрация больше концентрации собственных носителей заряда n_i при данной температуре, если же концентрация меньше n_i, то их называют неосновными носителями заряда. В области истощения примеси концентрация неосновных носителей заряда должна резко возрастать с температурой

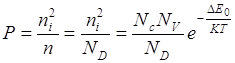
Последнее справедливо до тех пор, пока концентрация дырок остается много меньше концентрации электронов.

P<<n=N_D

Высокие температуры

С ростом температуры число дырок возрастает и может стать сравнимой с концентрацией электронов 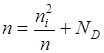 вся примесь ионизирована и необходимо учитывать ионизацию вещества.

Из уравнения

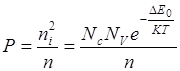
P=N_D или n=2N_DТемпература перехода к собственной концентрации, тем выше, чем больше  и чем больше концентрация примесей.

Акцепторный полупроводник.

Температурная зависимость на рисунке уровня Ферми в полупроводнике с акцепторной примесью.

Оценим температуру, при которой наступает истощение примеси.

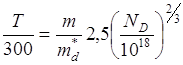
Когда вся примесь ионизирована:

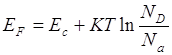
Когда вся примесь ионизирована и происходит ионизация основного вещества: n=N_D+P

Чем шире запрещенная зона и чем больше концентрация примеси, тем при большей температуре происходит переход к собственной проводимости.

Фотопроводимость

Ширину запрещенной зоны можно определить с помощью явления внутреннего фотоэффекта. Если полупроводник облучать монохроматическим светом, постепенно увеличивая частоту световой волны n, то, начиная с некоторой частоты, n₀, можно обнаружить возрастание электропроводности (фотопроводимость). Эта частота соответствует такой энергии фотона hn₀, при которой электрон в основной зоне, поглотив фотон, получает от него энергию, достаточную для перехода в зону проводимости. Это имеет место, если выполняется неравенство

Измеряя частоту света, при которой начинается рост электропроводности, можно получить . Получают хорошие результаты.

Эффект Холла в полупроводнике.

Физические явления, возникающие в веществе, находящемся в магнитном поле, при прохождении через вещество электрического тока под воздействием электрического поля, называют гальваномагнитными эффектами. Другими словами, гальваномагнитные явления наблюдаются в веществе при совместном действии электрического и магнитного полей. К гальваномагнитным явлениям относятся:

1)     эффект Холла;

2)     магниторезистивный эффект, или магнитосопротивление;

3)     эффект Эттингсгаузена, или поперечный гальванотермомагнитный эффект;

4)     эффект Нернота, или продольный гальванотермомагнитный эффект.

Эффект Холла называют также гальваномагнитным эффектом. Указанные выше названия «поперечный» и «продольный» гальванотермомагнитные эффекты отражают направления градиентов температуры относительно тока; по отношению к магнитному полю они могут быть поперечными или продольными.

Гальваномагнитные эффекты можно представить на основе рассмотрения движения заряженной частицы в электрическом и магнитном полях под действием силы Лоренца:

(1)

В параллельных электрическом и магнитном полях частица движется по винтовой линии с непрерывно возрастающим шагом. Частица имеющая в одном магнитном поле скорость V_парал вдоль поля и V_перп перпендикулярно полю, - вращается по окружности радиуса

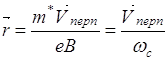(2)

с угловой скоростью 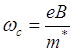 и перемещается вдоль поля со скоростью V_парал

Поскольку электрическое поле не влияет на V _перп, но меняет V_парал, становится очевидным, что движение происходит по винтовой линии с переменным шагом.

В поперечных (или скрещенных) полях  и  частица, не имеющая начальной скорости, движется по циклоиде: частица вращается окружности радиуса 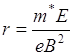 (3)

центр которой движется равномерно в направлении перпендикулярном электрическому и магнитному полям со скоростью дрейфа

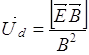 (4)

Если частица имеет начальную скорость V₀, лежащую в плоскости, перпендикулярной магнитному полю, то траекторией частицы является трахоида (удлиненная или укороченная циклоида).

Если скорость движущейся частицы имеет составляющую вдоль магнитного поля, то на эту составляющую скорости не оказывает воздействие ни электрическое, ни магнитное поля.

При движении частицы в твердом теле не6обходимо учесть соударения, которые нарушают направленное движение частиц под действием полей. После каждого соударения частица будет двигаться по винтовой линии или трахоиде, которое характеризуется новыми параметрами.

Для характеристики величины поля необходимо сравнить время релаксации с периодом вращения частицы под действием магнитного поля. Если время релаксации значительно превосходит период , то за время t частица совершит несколько оборотов, двигаясь по циклоиде или винтовой линии. Это возможно при больших магнитных полях. Если частица не совершает даже одного оборота за время t, то магнитные поля считаются малыми. Таким образом, в сильных полях

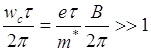(5)

в слабых полях

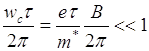(6)

Понятие «сильные» поля или «слабые» зависит не только от величины индукции магнитного поля В, но и от подвижности носителей заряда. Условия (5) и (6) можно связать с радиусом окружности r, по которому движется частица, и длиной свободного пробега l:

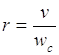
   (7)

Следовательно, в любых магнитных полях r >> 1 – траектория частицы искривляется незначительно, в сильных магнитных полях траектория изменяется очень сильно.

Для понимания одних явлений достаточно учесть только скорость дрейфового движения

в то время как для понимания других эффектов важно иметь в виду разброс скоростей электронов. Все это учитывается кинетическим уравнением, поэтому оно позволяет получить значительно более точное описание кинетических эффектов