Навигация
Найдём связь между изменениями давления и энтропии при постоянном значении внутренней энергии системы
2. Найдём связь между изменениями давления и энтропии при постоянном значении внутренней энергии системы
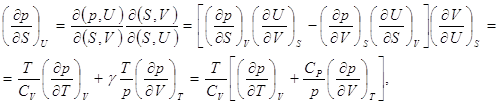 (7.2)
(7.2)
где использованы соотношения (2.7), (2.12), (2.17) и значения соответствующих частных производных от внутренней энергии. Нетрудно заметить, что для газов, при постоянном значении внутренней энергии, увеличение давления сопровождается уменьшением энтропии. Это и понятно, так как энтропия связана с вероятностью, а при увеличении давления уменьшается вероятность состояния системы.
3. Найдём связь между изменениями отдельных параметров системы при постоянном значении внутренней энергии.
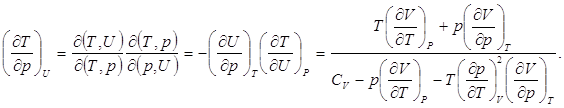 (7.3)
(7.3)
В случае идеального газа имеем:
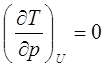 (7.4)
(7.4)
Этого и следовало ожидать, поскольку внутренняя энергия идеального газа зависит от температуры. Поэтому условию U=const соответствует T=const. Для реальных газов условие (7.4) не выполняется.
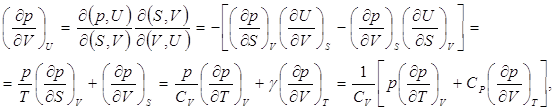 (7.5)
(7.5)
| Гч /-• ^ .6 |
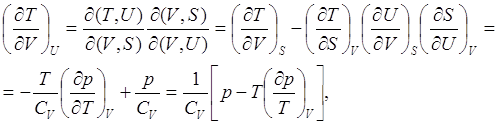 (7.6)
(7.6)
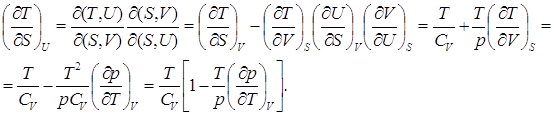 (7.7)
(7.7)
Нетрудно убедиться, что для идеального газа
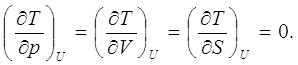 (7.8)
(7.8)
Найдём связь между изменениями отдельных параметров системы и её теплосодержанием.
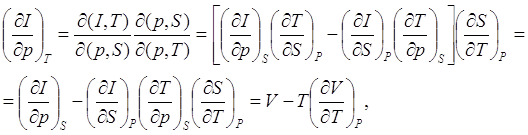 (7.9)
(7.9)
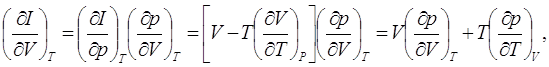 (7.10)
(7.10)
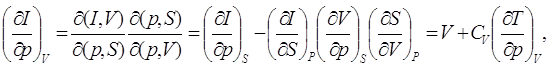 (7.11)
(7.11)
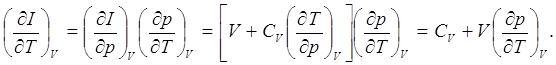 (7.12)
(7.12)
Однако это значение частной производной можно определить и более простым способом, если учесть, что I=U+pV и dI=dU+d(pV). Тогда
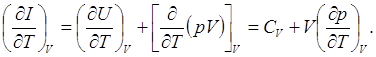
Важно подчеркнуть, что одно и то же значение частной производной, при постоянном значении выбранного параметра, можно получить несколькими способами в зависимости от выбора промежуточных переменных. Учитывая это, при решении задач, можно ввести такие якобианы, тождественно равные единице, которые относительно быстро приведут к цели. Покажем это на одном примере.
a) 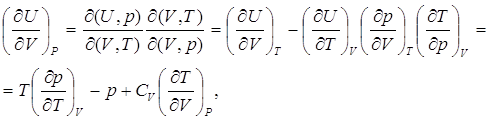 (7.13)
(7.13)
где были использованы (3.1) и (2.2).
b) 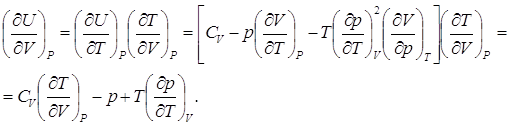 (7.14)
(7.14)
Аналогичное значение, но с помощью введения переменных S и p было получено ранее в выражении (6.9).
Приведённый пример показывает, что для проверки правильности нахождения одной и той же термодинамической величины можно использовать несколько вариантов, хотя и в данном примере использованы не все.
СПОСОБЫ ОПРЕДЕЛЕНИЯ CP ДЛЯ ИДЕАЛЬНОГО ГАЗА.Из объединённого выражения обоих начал термодинамики следует, что если подвод теплоты к системе осуществляется при изобарическом процессе, то TdS=CPdT, или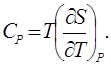
Однако, теплоемкость Cp для идеального газа можно определить как частную производную от тепловой функции по температуре. Действительно, при изобарическом процессе
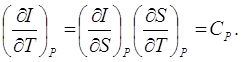 (8.1)
(8.1)
Это соотношение нетрудно понять, поскольку при р=const
dI=TdS+Vdp=TdS=CpdT.
Найдём связь между изменениями температуры и тепловой функции при изохорическом процессе.
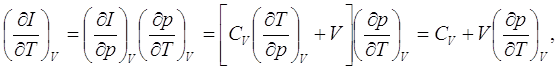 (8.2)
(8.2)
где учтено выражение (7.11).
В случае адиабатического процесса изменения тех же величин дают:
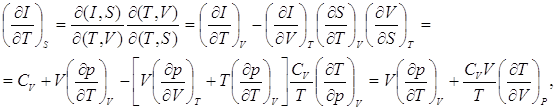 (8.3)
(8.3)
где использованы соотношения (2.2), (2.8), (7.10) и (8.2).
Непосредственной проверкой нетрудно убедиться, что для идеального газа
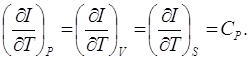 (8.4)
(8.4)
Читателям представляется возможность найти удовлетворительное, с точки зрения законов термодинамики, объяснение выражений (8.4).
По аналогии с вышеприведенными примерами, можно решить большое количество задач, связанных со свободной энергией, энтальпией и термодинамическим потенциалом Гиббса.
Вышеприведенные примеры убедительно доказывают преимущество такого подхода к решению задач термодинамики. Этим способом, в основном, решаются и задачи, связанные с термодинамикой стержней, диэлектриков и магнетиков, примеры которых приведены в [4] и [7], для которых можно учесть электро- и магнитострикционные явления, пьезоэлектрический и пьезомагнитный эффекты, а также и задачи, связанные с химическим потенциалом, когда количество вещества в системе изменяется .
Применение якобианов, особенно после изучения свойств термодинамических функций и их дифференциалов, позволяет более доступным способом решить ту или иную задачу, и, что очень важно, даёт возможность, даже при решении одной задачи, охватывать большой материал, предусмотренный программой. Преимущество такого подхода к рассмотрению отдельных, или группы, вопросов, как показали наши наблюдения, не вызывает сомнений как с точки зрения корректности математических выражений, так и логичности и взаимосвязи явлений термодинамики.
СОСТАВЛЕНИЕ ДЕТЕРМИНАНТОВ ЯКОБИ И ТАБЛИЦЫ ТЕРМОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ ДЛЯ СИСТЕМ, ОПИСЫВАЕМЫХ БОЛЬШИМ ЧИСЛОМ ПЕРЕМЕННЫХ.В качестве примера рассмотрим систему, описываемую тремя независимыми переменными, например, систему с переменным количеством вещества. В этом случае дифференциалы термодинамических функций имеют вид:
dU=TdS-pdV+mdN, (9.1)
dF=-SdT-pdV+mdN, (9.2)
dI=TdS+Vdp+mdN, (9.3)
dФ=-SdT+Vdp+mdN (9.4)
где dN – изменение числа молей вещества , а m – химический потенциал, имеющий размерность энергии в расчете на количество молей.
Из выражения (9.1) получим следующие соотношения:
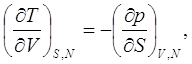 (9.5)
(9.5)
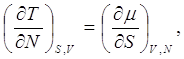 (9.6)
(9.6)
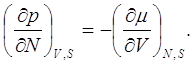 (9.7)
(9.7)
Формула (9.5) даёт:
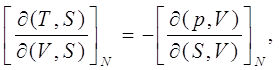
откуда
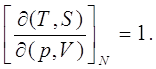 (9.8)
(9.8)
Из (9.6) и (9.7), аналогичным способом, получаем:
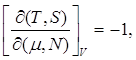 (9.9)
(9.9)
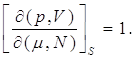 (9.10)
(9.10)
При рассмотрении дифференциалов свободной энергии (9.2) и энтальпии (9.3) получим, соответственно, следующие, новые, соотношения:
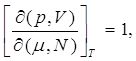 (9.11)
(9.11)
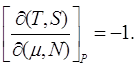 (9.12)
(9.12)
Уместно отметить, что рассмотрение дифференциала термодинамического потенциала Гиббса (9.4) не приводит к установлению нового соотношения. Раскрывая якобианы (9.8) – (9.12) получим:
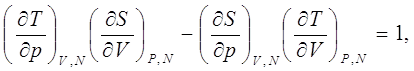 (9.13)
(9.13)
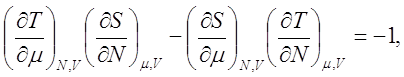 (9.14)
(9.14)
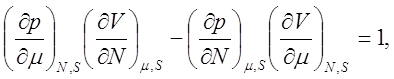 (9.15)
(9.15)
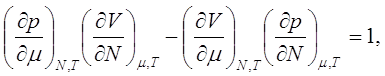 (9.16)
(9.16)
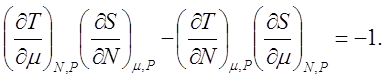 (9.17)
(9.17)
Все коэффициенты выражения (9.13) нами уже определены. Из формул (9.14)–(9.17) составим таблицу термодинамических коэффициентов так, чтобы первая строка не содержала S и р , вторая- S и V , третья- V и Т, четвертая- Т и р.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Устанавливая соответствующую связь между коэффициентами данной таблицы, мы окажемся в состоянии решить все задачи, связанные с однокомпонентной системой, с переменным количеством вещества.
Аналогичным образом составляется таблица коэффициентов для систем, описываемых четырьмя и большим числом независимых переменных, например, для двух- или трёхкомпонентной термодинамической системы.
Если процессы, протекающие в многокомпонентной системе таковы, что
dp=dV=dT=dS=0 (9.19)
| (9.20) |
и
![]() (9.20)
(9.20)
то будем иметь дело с системой, для которой
dU=dF=dI=dФ=0 (9.21)
При выполнении условия (9.19) можно рассматривать только один термодинамический потенциал, при этом неважно выполняется условие (9.20) или нет.
Полезно заметить, что в реальных условиях возможны состояния, при которых условия (9.19)–(9.21) не соблюдаются и тем не менее при неизменных р и Т или V и V мы в течение длительного времени не наблюдаем изменения равновесия системы. Такое равновесие называется ложным (об этом более подробно см. в [8]). При условии
![]() (9.22)
(9.22)
возможен самопроизвольный процесс в прямом направлении в любой гомогенной или гетерогенной системе (например, переход отдельных компонент из одной фазы в другую, возможность протекания химических реакций между различными компонентами и т. д.).
Отметим, что переход данного компонента может происходить самопроизвольно только из фазы, для которой его химический потенциал больше, в фазу, для которой он меньше. Такой переход сопровождается уменьшением химического потенциала компонента в первой фазе и увеличением его во второй. В результате этого разность между химическими потенциалами данного компонента в этих двух фазах уменьшается и когда значения химического потенциала компонент в обеих фазах выравниваются, достигается состояние равновесия.
ЛИТЕРАТУРА1. В.Г.Левич, Курс теоретической физики, t.1, стр. 446, "Наука", 1969.
2. В.И.Смирнов, Курс высшей математики, т.3, ч.2, "Наука", 1974.
3. Д. Тер Хаар, Г.Вергеланд, Элементарная термодинамика, "Мир", 1968.
4. Ю.Б.Румер, М.Ш.Рыбкин, Термодинамика, статистическая физика и кинетика, "Наука",1977.
5. В.И.Тюлин, Введение в теорию излучения и распространения звука, стр.17, "Наука", 1976.
6. Ч.Киттель, Статистическая термодинамика, стр.147, "Наука",1977.
7. Р.Кубо, Термодинамика, "Мир" , 1970.
8. Л.В.Радушкевич, Курс термодинамики, стр.192, "Просвещение", 1971.
СОДЕРЖАНИЕКраткое введение ................………………..………………………………………….. 3
Термодинамические коэффициенты и установление связи между ними…………. 6
Вывод уравнения адиабатического процесса для идеального и реального газов .... 11
Вывод уравнения для вычисления скорости распространения звука в среде………. 13
Способы определения СV для идеального газа ………………………………………... 15
Об изменениях внутренней энергии при других изопроцессах……………………… 17
Вывод некоторых полезных термодинамических соотношений……………………. 21
Способы определения СР для идеального газа………………………………………… 26
Составление детерминантов Якоби и таблицы термодинамических коэффициентов для систем, описываемых большим числом переменных………………………………….. 28
Литература………………………………………………………………………………… 33
Похожие работы
... сложным физическим понятием для учащихся. К этому понятию учащихся подводят на основе опытов по электризации тел. На основе опытов по электризации различных тел (стекла, эбонита, капрона, и т.д.) ищут ответ на следующие вопросы: 1. Только ли эбонит при натирании шерстью электризуется? 2. Обязательно ли натирать тела шерстью? 3. Электризуются оба или одно из натертых тел? 4. Зависит ли род заряда ...
... (молекулярно-кинетическая) и энергия взаимодействия молекул (молекулярно-потенциальная) являются частью внутренней энергии тела. Такой подход правомерен и с научной точки зрения, так как тепловые явления, изучаемые в школе, протекают в пределах среднего температурного диапазона, при котором изменение внутренней энергии тел связано главным образом с изменением кинетической и потенциальной энергии ...
... в другую. Процессы переноса теплоты представляют собой процессы обмена внутренней энергией между элементами рассматриваемой системы в форме теплоты. Общая характеристика и формулировка второго закона термодинамики Естественные процессы всегда направлены в сторону достижения системой равновесного состояния (механического, термического или любого другого). Это явление отражено вторым законом ...
... одного состояния в другое, получили название термодинамических потенциалов. Каждый из термодинамических потенциалов является однозначной функцией состояния системы. В термодинамике понятие термодинамического потенциала относят ко всей системе в целом (тогда как в физике обычно имеют дело с удельным потенциалом). Произведение называют иногда «связанной энергией». Это название станет понятным, ...
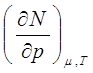
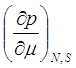
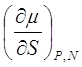
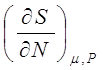



0 комментариев