Навигация
Определение закона изменения внешнего момента, обеспечивающего постоянство угловой скорости
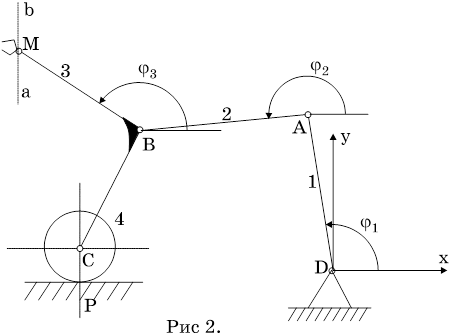
3.2 Определение закона изменения внешнего момента, обеспечивающего постоянство угловой скорости
При действии внешнего момента ![]() , обеспечивающего равномерное вращение механической системы вокруг шарнира
, обеспечивающего равномерное вращение механической системы вокруг шарнира ![]() , последнее слагаемое в левой части равенства (3.1.9) обращается в нуль:
, последнее слагаемое в левой части равенства (3.1.9) обращается в нуль:
![]() ,
, ![]() ; отсюда
; отсюда ![]() .
.
Тогда выражение (3.1.9) примет вид:
![]() (3.2.1)
(3.2.1)
![]() направлен противоположно главному моменту внешних сил, то есть, против часовой стрелки.
направлен противоположно главному моменту внешних сил, то есть, против часовой стрелки.
Внешний момент, обеспечивающий равномерное вращение конструкции, равен:
![]() (3.2.2)
(3.2.2)
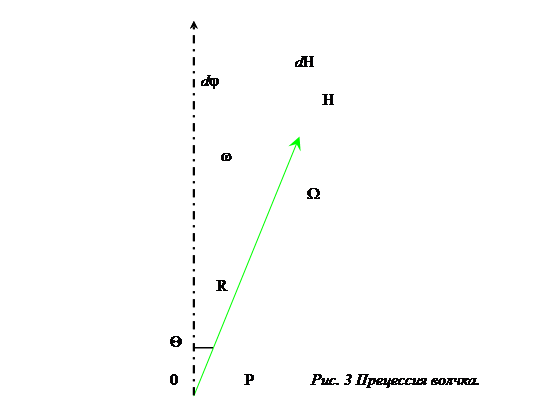
В приложении к курсовой работе изображён график зависимости ![]() (рис. 3).
(рис. 3).
4. Определение реакций в опорах вращающегося тела
Определим реакции в опоре вращающегося тела методом кинетостатики. Он заключается в решении задачи динамики средствами (уравнениями) статики. Для каждой точки механической системы справедливо основное уравнение динамики:
![]() (4.1)
(4.1)
Здесь ![]() и
и ![]() – масса и ускорение некоторой точки системы;
– масса и ускорение некоторой точки системы; ![]() – сумма всех активных сил и реакций связей, приложенных к ней.
– сумма всех активных сил и реакций связей, приложенных к ней.
Основному уравнению динамики (4.1) можно придать вид уравнения статики:
![]() (4.2)
(4.2)
Здесь ![]() – сила инерции точки механической системы.
– сила инерции точки механической системы.
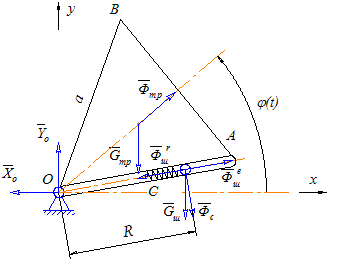
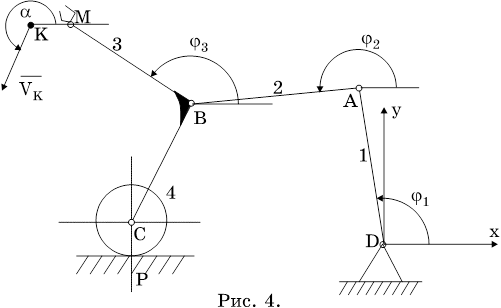
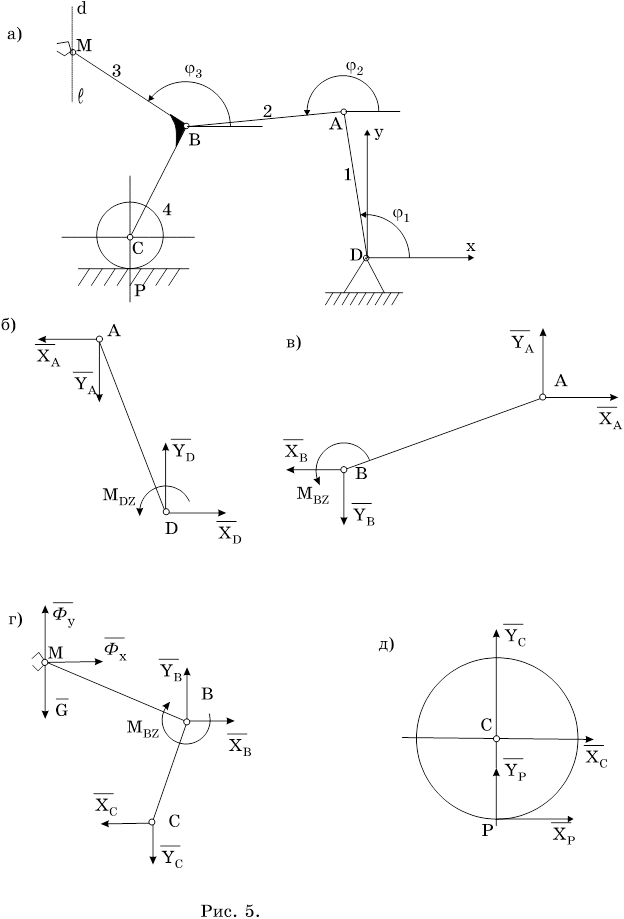
Рисунок 4.1. Определение реакций в опорах вращающегося тела
Для заданной механической системы уравнение статики (4.2) имеет вид:
![]() (4.3)
(4.3)
Для определения реакции шарнира нам необходимо и достаточно взять за координатные оси – неподвижные оси ![]() и
и ![]() , и определить составляющие реакции шарнира на эти оси:
, и определить составляющие реакции шарнира на эти оси:
![]()
![]() (4.4)
(4.4)
Отсюда:
![]()
Подставив значения сил, получим:
![]() (4.5)
(4.5)
Теперь спроецируем (4.2) на неподвижную ось ![]() :
:
![]()
![]() (4.6)
(4.6)
Отсюда:
![]()
Подставив известные значения сил, получим:
![]() (4.7)
(4.7)
Полную реакцию в шарнире ![]() можно найти по формуле:
можно найти по формуле: ![]() , где
, где ![]() и
и ![]() определяются выражениями (4.5) и (4.7); график её зависимости от времени приведён в приложении к курсовой работе (рис. 4).
определяются выражениями (4.5) и (4.7); график её зависимости от времени приведён в приложении к курсовой работе (рис. 4).
5. Исследование движения механической системы с двумя степенями свободы с помощью уравнений Лагранжа II рода
5.1 Составление уравнений движения системы методом Лагранжа
Уравнения второго рода являются одним из наиболее удобных приёмов составления уравнений движения механических систем. Они имеют следующий вид:
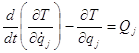
![]() (5.1.1)
(5.1.1)
Здесь ![]() – кинетическая энергия системы;
– кинетическая энергия системы; ![]() ,
, ![]() ,
, ![]() , – обобщённые координаты, скорости и силы соответственно;
, – обобщённые координаты, скорости и силы соответственно; ![]() – число степеней свободы.
– число степеней свободы.
Уравнения (5.1.1) образуют систему ![]() уравнений второго порядка относительно
уравнений второго порядка относительно ![]() функций
функций ![]() , а порядок данной системы равен
, а порядок данной системы равен ![]() . Форма уравнений Лагранжа не зависит от выбора обобщённых координат
. Форма уравнений Лагранжа не зависит от выбора обобщённых координат ![]() . В связи с этим говорят, что уравнения Лагранжа второго рода обладают свойством инвариантности.
. В связи с этим говорят, что уравнения Лагранжа второго рода обладают свойством инвариантности.
Как видно из (5.1.1), для получения уравнений Лагранжа необходимо найти соответствующие производные от кинетической энергии системы и определить обобщённые силы.
Определим кинетическую энергию системы. Она будет складываться из кинетических энергий треугольника и шарика: ![]() .
.
![]()
Подставив значение ![]() из (3.1.5), получим:
из (3.1.5), получим:
![]() (5.1.2)
(5.1.2)
Кинетическая энергия шарика определяется его массой и относительной и переносной скоростями:
![]()
С учётом известных значений скоростей, получим:
![]() (5.1.3)
(5.1.3)
Кинетическая энергия системы равна:
![]() (5.1.4)
(5.1.4)
Найдём производные от кинетической энергии согласно (5.1.1):
![]()
![]() (5.1.5)
(5.1.5) ![]() (5.1.6)
(5.1.6)
![]()
![]() (5.1.7)
(5.1.7) ![]() (5.1.8)
(5.1.8)
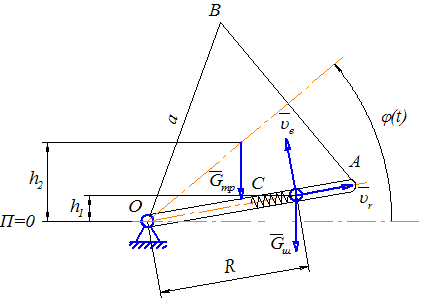
Рисунок 5.1.1. Определение кинетической и потенциальной энергий системы
Теперь, исходя из (5.1.1), нужно определить обобщённые силы. Данная механическая система является консервативной, мы можем определить обобщённые силы через потенциальную энергию по формуле:
![]() (5.1.9)
(5.1.9)
Найдём потенциальную энергию. Она будет складываться из работ консервативных сил по перемещению тела из нулевого положения: ![]() . За нулевой уровень потенциальной энергии выберем начальный момент времени, при
. За нулевой уровень потенциальной энергии выберем начальный момент времени, при ![]() :
:
![]() – энергия положения шарика;
– энергия положения шарика;
![]() – энергия положения прямоугольника;
– энергия положения прямоугольника;
![]() – потенциальная энергия силы упругости;
– потенциальная энергия силы упругости;
Потенциальная энергия системы равна:
![]() (5.1.10)
(5.1.10)
Найдём обобщённые силы:
![]() (5.1.11)
(5.1.11)
![]() (5.1.12)
(5.1.12)
Теперь можем записать систему уравнений Лагранжа II рода:
![]() (5.1.13)
(5.1.13)
![]() (5.1.14)
(5.1.14)
Похожие работы
... производные в уравнения Лагранжа (11): или (j=1,2,…, s). (12) Уравнения (12) называются уравнениями Лагранжа второго рода для консервативной системы. 7 Применение уравнений Лагранжа II рода к исследованию движения механической системы Массы тел механической системы m= 2m; m= 6m; m=m. Начальные условия:,,,. Найти уравнения движения системы в обобщенных координатах ,. Для ...
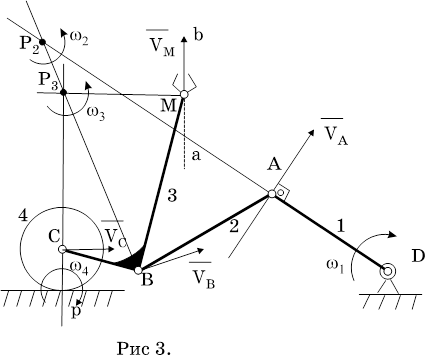
(3) w3z=w3z (j1, j2, j3, VM); w4z=w4z (j1, j2, j3, VM) или Vc=Vc (j1, j2, j3, VM) Из уравнений (3) определяют угловые скорости звеньев для фиксированного момента времени при заданных в этот момент значениях j1, j2, j3. Изменение j1, j2, j3, а следовательно и w1z, w2z, w3z во времени определится,если дополнить систему (3) уравнениями: ...
... и выдвигает новое определение: все системы, допускающие несводимое вероятностное описание, по определению считаются хаотическими [1, с.9]. 3. БРЮССЕЛЬСКАЯ ИНТЕРПРЕТАЦИЯ КВАНТОВОЙ МЕХАНИКИ Э.Шрёдингер 3.1 Альтернативные интерпретации квантовой механики Вероятно, квантовая механика – одна из немногих, если не единственная работающая физическая теория, по поводу интерпретации которой ...
... более прозаично связаны с периодическими колебаниями физических систем и воздействием на них сторонних сил, имеющих также физическую природу. Итак, природные катаклизмы вызываются периодическими колебаниями системы атмосфера – океан – Земля под воздействием Солнца (прецессия), неравномерности прогрева атмосферы (воздействие воздушных масс на Землю), неравномерным прогревом океана (океанические ...
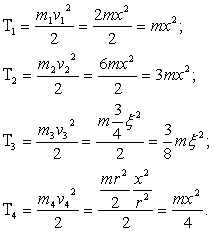
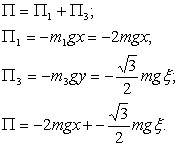

0 комментариев