Навигация
Классическая «Математика в девяти книгах»
1. Классическая «Математика в девяти книгах».
«Математика в девяти книгах» (Цзю чжан Суань шу) – центральное сочинение математического «Десятикнижья». Самое большое по объёму и самое содержательное, оно является одним из замечательных памятников древнего Китая времени династии Ранней Хань (206 г. до н.э. – 7 г.н.э.), правившей в одной из обширных и могущественнейших империй древнего мира.
Математический материал: правила действия дробями, алгоритм Евклида, пропорции и прогрессии, правила извлечения корней, вычисление различных площадей и объёмов, теорему Пифагора и применение подобия прямоугольных треугольников, формулы для пифагоровых чисел, вопросы практической геометрии, решение системы линейных уравнений и т.д.
Сочинение состоит из девяти довольно самостоятельных книг:
книга I «Измерение полей»;
книга II «Соотношение между различными видами зерновых культур»;
книга III «Деление по ступеням»;
книга IV «Шао-гуан» (метод извлечения квадратных кубических корней);
книга V «Оценка работ»;
книга VI «Пропорциональное распределение»;
книга VII «Избыток-недостаток»;
книга VIII «Правило фен-чен»;
книга IX «Соотношение между катетами и гипотенузой в прямоугольном треугольнике».
«Математика в девяти книгах» является первым собственно математическим сочинением из ряда классических в древнем Китае.
2. Сочинение Лю Хуэя по практической геометрии.
Лю Хуэй, математик III в. н.э., известен как основной комментатор «Математики в девяти книгах». Он обозначил метод решения – чжун-ча, т.е. «двухсловная разность» в самостоятельном трактате – « Математический трактат о морском острове». Этот трактат содержит девять задач. Они, по-видимому, сыграли большую роль в науке.
3. Метрологический трактат Сунь-цзы.
Историки установили, что это сочинение не принадлежит знаменитому древнекитайскому полководцу V в. до н.э. Сунь-цзы. Композиция: три книги-цзюня содержит 64 задачи.
4. Математический трактат Чжан Цю-цзяня.
Этот трактат написан примерно через 200 лет после написания «Метрологический трактат Сунь-цзы». Математический трактат Чжан Цю-цзяня – второй по размеру текст в «Десятикнижьи» после «Математики в девяти книгах». Он состоит из трёх книг: первой, средней, последней. Всего в них 92 задачи.
5. Практическое руководство для чиновников пяти ведомств.
Небольшой анонимный «Математический трактат пяти ведомств» относится приблизительно к IV в.
6. Арифметическое пособие Сяхоу Яна.
Текст относится к середине VI в. Трактат состоит из трёх книг, он выделяется особым стремлением к облегчению производства операций на счётном приборе. Всего 73 задачи, причём в первой книге нет задач.
7. Два трактата Чжень Луаня.
Чжень Луань жил в VI столетии н.э., был астрономом во время династии Северная Чжоу (557-583) и участвовал в состоянии календаря Тяньхе. Он изучил буддизм и написал «Трактат о весёлом пути» в трёх свитках. Чжень Луэнь – составитель и комментатор математического «Десятикнижья», автор одного из трактатов этого сборника: «Искусство счёта в Пятикнижие».
8. Трактат Ван Сяо-туна об уравнениях третьей степени.
Весь трактат в целом посвящён чётко одной проблеме – численному решению уравнений третьей степени, а также биквадратных уравнений. Он состоит из трёх групп задач. Ван Сяо-тун употреблял специальную терминологию, возможно принадлежащую ему или общеупотребительную в его время.
9. Трактат о гномоне.
«Математический трактат о Чжоу-би» - самый ранний текст из сохранившихся по истории китайской математики. Он состоит из двух свитков: верхнего и нижнего.
Таким образом, на протяжении пяти столетий были составлены и обработаны все десять трактатов математического «Десятикнижья».
Математика Китая
Техника Вычислений.
Мало известна техника вычислений древнего Китая, которую иногда совсем не упоминают, хотя существенным образом дополняет общую картину развития математики в древности.
Китайская техника счёта была основана на десятичной нумерации, но пользовались позиционным принципом. В древнем Китае большую роль играла счётная доска с осуществлённой на ней позиционной системой счисления.
Китайские источники существенным образом дополняют общую картину развития вычислительных методов в древности. Они позволяют более полно выяснить различные вопросы, например:
- система счисления;
- арифметика целых чисел;
- десятичные дроби;
Понятия числа. Арифметические и теоретико-числовые проблемы.
Здесь рассматривается алгебраический путь перехода от целых чисел к числам рациональным. Тот исторический процесс, который происходил в древнем Китае при освоении понятия числа, носил достаточно общий характер и имел место во всех древних цивилизациях:
- обыкновенные дроби;
- пропорции и прогрессии;
- проблема деления с остатком.
Алгебра. Решение уравнений.
Алгебраические методы характерны для китайской математики. Достижение китайских алгебраистов – наиболее известная часть истории математики в Китае, известная, однако не в полной мере. Заметим, что древняя алгебра излагалась словесно, без символики:
- линейные системы;
- решение уравнений высших степеней численным методом;
Геометрия. Применение алгебраических методов к геометрическим задачам.
Здесь рассматривались методы, которыми пользовались при решении различных задач прикладного характера. Существует обоснованный взгляд на китайскую математику как на вычислительную, для которой характерны алгебраические методы:
- измерение площадей и объёмов;
- теорема Пифагора;
- измерение круга и шара;
- определение расстояний до недоступных предметов.
Заключение
На основании всего вышеизложенного можно сделать вывод о том, что развитие математики в древнем Китае со II в. до н.э. по VII в.н.э. дало сильный толчок для дальнейшего её совершенствования и применение разработанных методов в будущем.
Зарождение группового десятичного счёта и мультипликативного принципа фиксирования чисел ещё в эпоху Инь, изобретение в дальнейшем счётной доски для проведения на ней вычислений привело к появлению позиционной системы счисления вместе с десятичными дробями.
В создании исчислений обыкновенных и десятичных дробей в дальнейшем проявились два различных направления в развитии математики. Первое направление – аналитическое – связано с десятичными дробями, метрологическое происхождение которых в древнекитайской математики находит объяснение в процедуре деления, а также извлечения корней. Второе алгебраическое – связано с обыкновенными дробями и теоретико-числовыми проблемами.
Были хорошо известны среднее арифметическое двух или нескольких чисел, свойства арифметической и геометрической прогрессии, учение о чётных и нечётных, а также о числовых «другой природы». Арифметика остатков, терема Пифагора, конечные числовые последовательности с первыми и вторыми разностями, магические квадраты с их трансформациями и т.д. – всё это свидетельствует об огромной практике в решении теоретико-числовых задач.
Что касается общей модели древней математики, то следует отметить её «линейность» как основу многих методов.
Список литературы
1. Березкина Э.И. Математика древнего Китая/ «Наука», М, 1980 г (с.48-50);
2. Математический энциклопедический словарь/ «Большая Российская Энциклопедия», М, 1995 г (с. 16 – 17);
3. Стройк Д.Я Краткий очерк истории математики/ издание третье/ «Наука», М, 1978 г.
Похожие работы
... , что процессы развития математики как науки на Западе значительно отличались от тех же процессов в странах Востока, Средней Азии и Ближнего Востока. II. Развитие математики в Древнем Китае Наличие у китайских математиков высокоразработанной техники вычислений и интереса к общим алгебраическим методам обнаруживает уже «Математика в девяти книгах» составленная по более ранним источникам ...
... и статьи из журналов “Квант”, “Математика в школе” и других периодических изданий, а также энциклопедические словари. Приложение 3. Вопросы к зачету по курсу “Математика” для студентов I курса исторического факультета СГУЧасть 1. Математика.Понятие множества; элементы множества; мощность множества; отношения принадлежности и включения. Виды множеств. Числовые множества. Операции над множествами, ...
... н.э.. О его жизни известно мало. Книга “Мо-цзы” –плод коллективного творчества моистов. Моизм просуществовал два века.2 Школа моистов во многом отличалась от других философских школ Древнего Китая: Мо-цзы остался единственным выдающимся ее представителем: его философия не оплодотворяла других учений; при Мо-цзы и позднее школа была четко построенной военизированной организацией, неукоснительно ...
... структура, манера изложения — все жестко регламентировалось, любые отклонения от стандарта считались нарушением нормы, порицались и запрещались. Наука - престижно только гуманитарное знание Жители Древнего Китая к знанию и мудрецам относились с почтением, однако под знанием в Поднебесной понимались постулаты почти исключительно из сферы гуманитарных дисциплин. Другие науки — точные, естественные ...

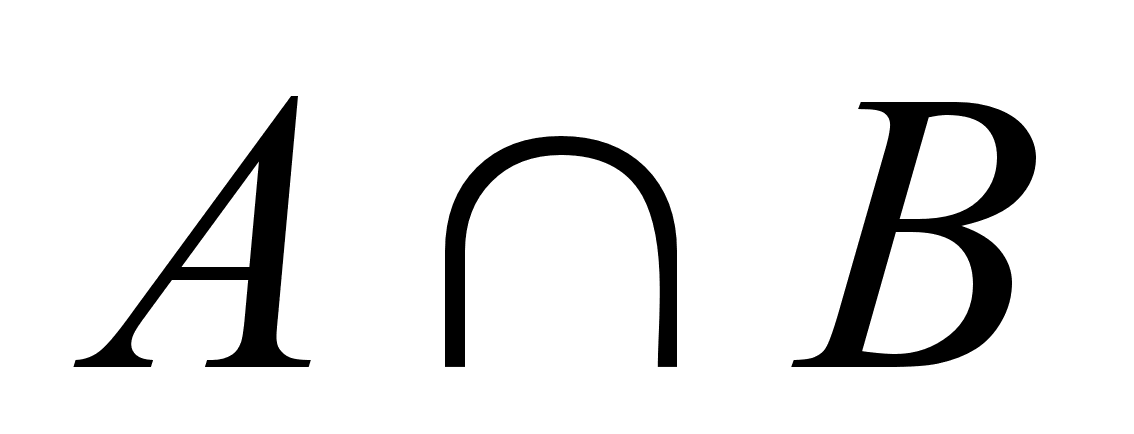
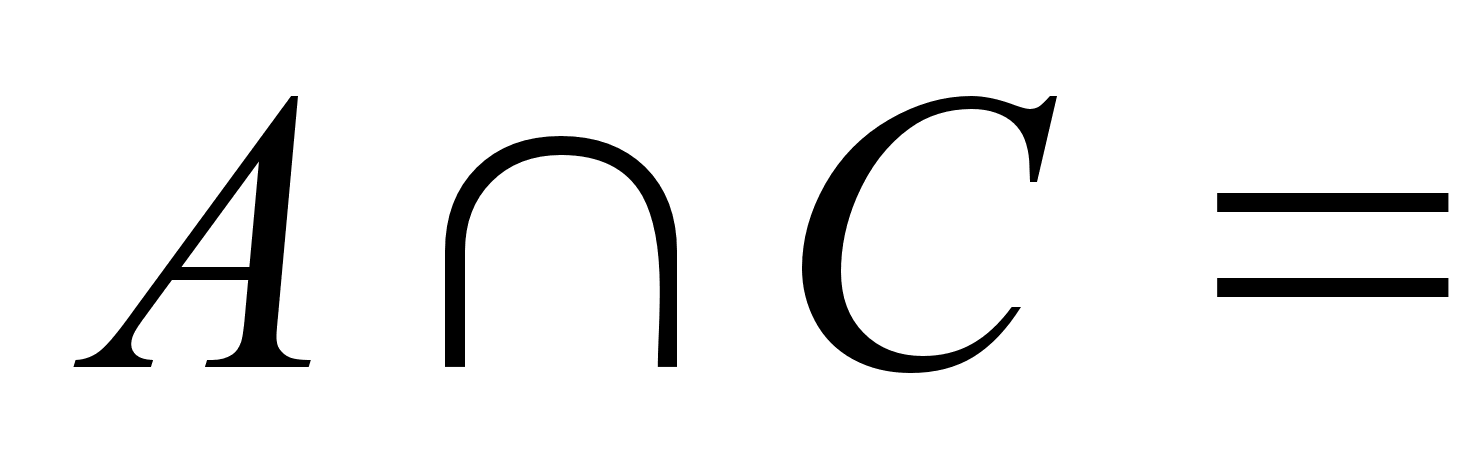
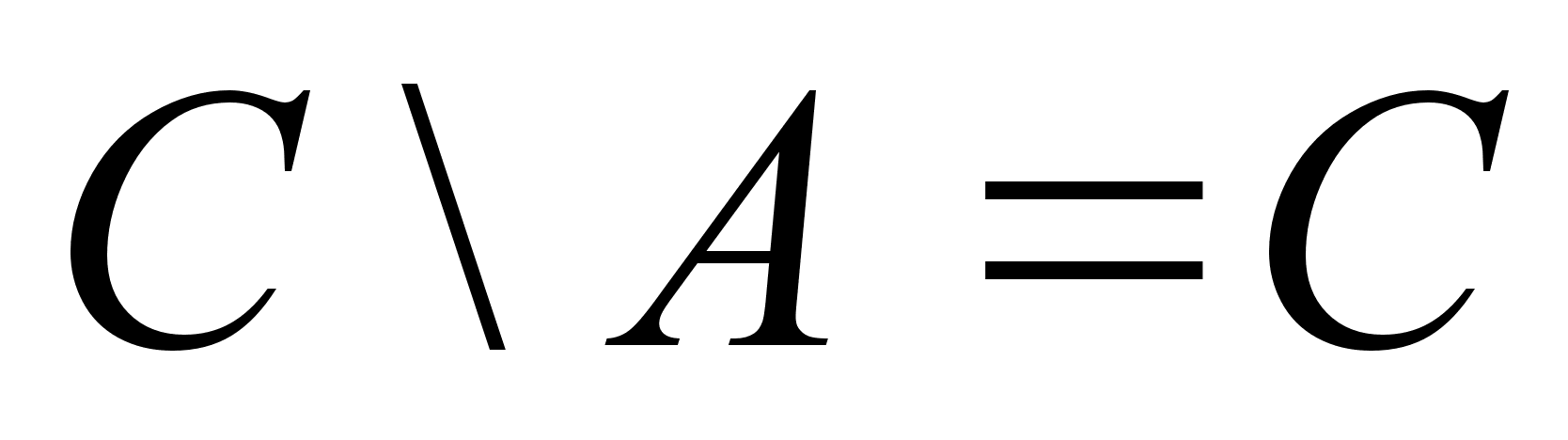






0 комментариев