Навигация
Оценка математического ожидания
1. Оценка математического ожидания
Проверяем
Ø состоятельность оценки для каждого стационарного «куска» ряда.
![]() ,
,
где ![]() – математическое ожидание на стационарном периоде
– математическое ожидание на стационарном периоде
![]() – среднее значение в зависимости от числа данных
– среднее значение в зависимости от числа данных
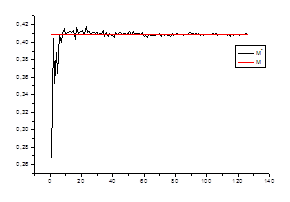



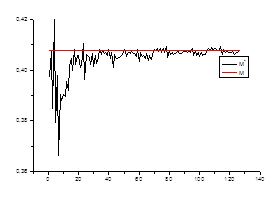

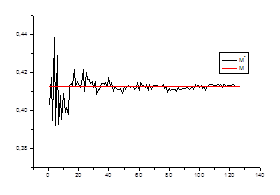
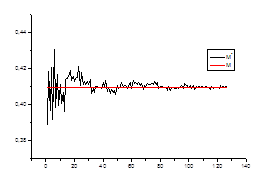
Ø несмещенность оценки
M [a*] = a,
| Номер интервала | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| M [a*] | 0,40938 | 0,41218 | 0,41058 | 0,41152 | 0,40758 | 0,41118 | 0,41259 | 0,40985 |
| a | 0,40714 | 0,40661 | 0,40437 | 0,4080 | 0,40492 | 0,40906 | 0,41206 | 0,41018 |
2. Оценка дисперсии
Проверяем
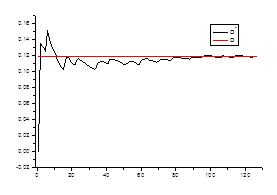
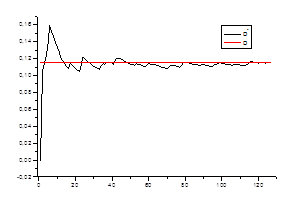
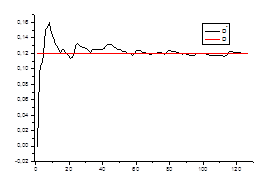
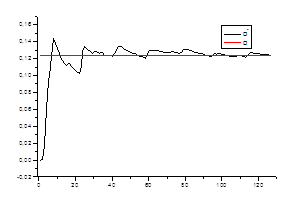
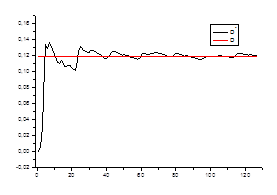
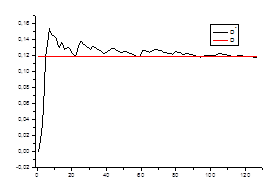
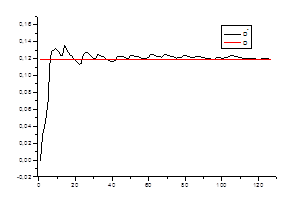
Ø состоятельность оценки для каждого стационарного «куска» ряда.
![]() ,
,
где ![]() – среднеквадратичное отклонение на стационарном периоде
– среднеквадратичное отклонение на стационарном периоде
![]() - среднеквадратичное отклонение в зависимости от числа данных
- среднеквадратичное отклонение в зависимости от числа данных

Ø несмещенность оценки
M [a*] = a,
| Номер интервала | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| M [a*] | 0,11862 | 0,11507 | 0,11944 | 0,1235 | 0,12227 | 0,11891 | 0,11709 | 0,1185 |
| a | 0,11477 | 0,11391 | 0,12122 | 0,11959 | 0,11959 | 0,11674 | 0,12163 | 0,11842 |
3. Вычислить куммулятивную частоту превышения уровня и сделать оценки ее стационарности
![]() – куммулятивная частота превышения уровня а.
– куммулятивная частота превышения уровня а.
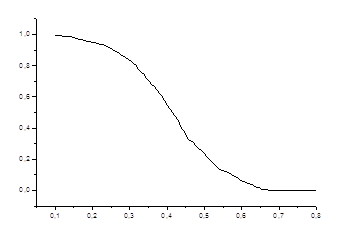
Рис. 3.1. Зависимость куммулятивной частоты от уровня превышения.
Разбиваем исходный ряд на на ![]() отрезков, для каждого «куска» ряда строим функции зависимости куммулятивной частоты от уровня превышения, и оцениваем стационарность полученных
отрезков, для каждого «куска» ряда строим функции зависимости куммулятивной частоты от уровня превышения, и оцениваем стационарность полученных
n-зависимостей критериям, полученным в п. 2.
Анализируя оценки корреляционной функции, математического ожидания и дисперсии, находим период стационарности куммулятивной частоты превышения уровня T=17.85 лет.

Рис. 3.2. Оценка корреляционной функции

Рис. 3.3. Оценки математического ожидания и дисперсии.
4. С помощью пуассоновской статистики дать долгосрочный прогноз превышения уровня. На какой срок Вы гарантируете такой прогноз?
![]()
– искомая формула вероятности того, что за период времени T произойдет ровно m превышений уровня a. Вероятность возникновения таких ситуаций определяется средней частотой превышения уровня a и временем прогноза. Из анализа данных за 176 лет на стационарном периоде находим функцию зависимости средней частоты от уровня a ![]() .
.

Рис. 4.1. Средняя частота превышения уровня
Нас интересуют редкие события, например, превышение уровня ![]() . Соответственно, среднюю частоту превышения такого уровня можно определить из графика
. Соответственно, среднюю частоту превышения такого уровня можно определить из графика ![]() , и она равна
, и она равна ![]() 0.0635
0.0635
Зная среднюю частоту, теперь можно вычислить вероятность того, что за период, например, равный 220 лет, произойдет ровно 1,2,3,4.

Рис. 4.2. Вероятность возникновения ровно m – аварий
Зависимости вероятности от прогнозируемого времени для разного числа превышения уровня (m=1,2,3,4) являются немонотонными, и их максимум приходится на моменты времени ![]()
Как видно из графика, сначала более вероятным является только одно превышение уровня a=0.6, затем два, три…
Например, вероятность того, что за 62 года произойдет три превышения уровня a=0.6, самая высокая и равна p= 0,19775.
5. Рассчитайте среднюю частоту появления выбросов и среднее время выброса
Будем рассматривать выбросы (превышение уровня, например, a=0.6) за период, на котором исходный ряд стационарен.
Выброс характеризуется следующим условием
![]()
Тогда можем найти среднюю частоту выброса за уровень а=0.6 ![]() =0.063
=0.063
Средняя продолжительность выброса для стационарных случайных процессов
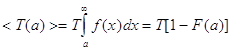
Отсюда, зная функцию распределения случайной величины, порог, начиная с которого процесс ведет к катастрофе, и период прогноза, можно рассчитать среднее время катастрофической ситуации, в нашем случае – превышение заданного уровня.
Среднее число выбросов за период T для стационарного процесса определяется:
![]()
где P – среднюю частоту выброса
Таким образом, среднее число катастроф пропорционально продолжительности времени прогноза и падает с увеличением порогового значения, определяющего возникновение катастрофической ситуации.
Средняя продолжительность выброса может быть вычислена по формуле
![]()
и она не зависит от прогнозируемого времени (для стационарных процессов
Средняя продолжительность выброса за уровень а=0.6 равна ![]() лет.
лет.
6. Попытайтесь сделать краткосрочный прогноз уровня воды, используя линейный и корреляционный анализ. Проверьте его на уже имеющихся данных
1. Линейный прогноз.
Рассматриваем наш ряд на стационарном периоде T. Выбираем n=127 точек. Тогда
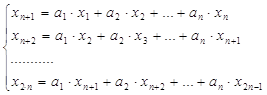
Нам известны значения ![]() . Решая систему уравнений, находим коэффициенты
. Решая систему уравнений, находим коэффициенты ![]() .
.
Тогда можем спрогнозировать любую точку ряда, например, ![]() :
:
![]()
В качестве проверки найденных коэффициентов сделали прогноз с 22-ого по 33-ий год (рис. 6.1) и c 33-ого по 44-ий год (рис. 6.2).
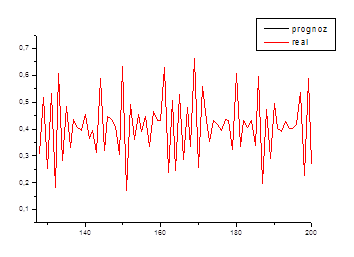
Рис. 6.1. Линейный прогноз с 22-ого по 33-ий год

Рис. 6.2. Линейный прогноз с 33-ого по 44-ый год
2. Корреляционный прогноз
Рассматриваем наш ряд на стационарном периоде T. Тогда можем представить в виде
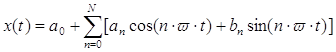
где
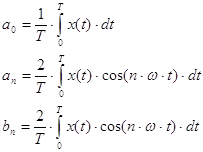
Зная коэффициенты ![]() и
и ![]() можно спрогнозировать уровень воды, например, на 33 года.
можно спрогнозировать уровень воды, например, на 33 года.
В качестве проверки найденных коэффициентов сделали прогноз на первые 22 года (рис. 6.3) и с 22-ого по 33-ий год (рис. 6.4). Как видно из графиков. Результаты совпадают в пределах погрешности.

Рис. 6.3. Корреляционный прогноз на первые 22 года

Рис. 6.4. Корреляционный прогноз с 22-ого по 33-ий год
Анализируя полученные результаты и используя уже известные данные, можно сказать, что корреляционный прогноз более точный.
Похожие работы
... примера Упрощённое уравнение для расчёта температурного режима реки. Температурный режим водных потоков описывается уравнением теплопроводности Фурье –Кирхгофа: Математическое моделирование глобального развития: В настоящее время проблема “Человек и среда его обитания” широко обсуждается во всём мире. Рост населения, истощение природных ресурсов, отрицательные воздействия человека на окружающую ...
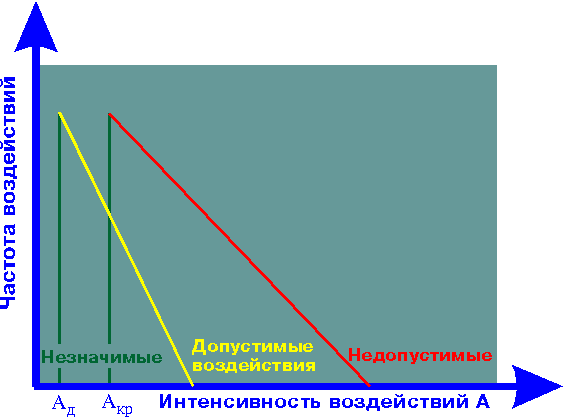
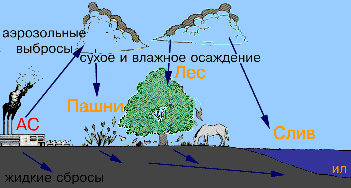
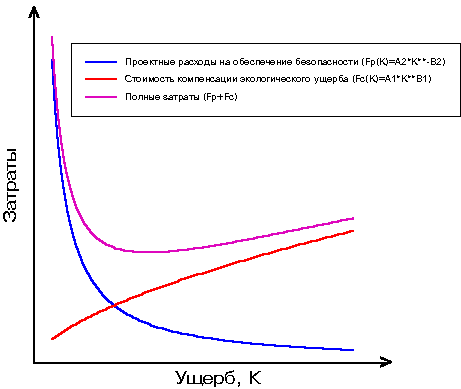
... , должны учитывать и синергетические, т.е. перекрестные эффекты. Однако этого, по-видимому, недостаточно. Для эффективной защиты окружающей среды необходимо законодательно ввести принцип ограничения вредных техногенных воздействий, в частности выбросов и сбросов опасных веществ. По аналогии с принципами радиационной защиты человека, упомянутыми выше, можно сказать, что принципы защиты окружающей ...
... работ – эксперимент по конвекции в жидком гелии (1979). Работа Фейгенбаума стимулировала также изучение и ренормгрупповое описание [10]. § 2. Развитие методов реконструкции математических моделей динамических систем Математические модели являются одним из основных инструментов познания человеком явлений окружающего мира. Под математическими моделями понимают основные закономерности и связи, ...
... контроля за состоянием окружающей среды, при контроле состояния окружающей среды недостаточно полно используются современные информационные технологии, в связи с чем основные направления совершенствования системы управления охраной окружающей среды в Юго-Западном районе должны быть сосредоточены именно в сфере информатизации данного процесса. 2. Исследование методов оценки загрязнения окружающей ...
0 комментариев