Вычисляют параметры основной и расширенной систем (ортогональные базисы, их веса, минимальные псевдоортогональные числа с их рангами и кратности)

1.         Вычисляют параметры основной и расширенной систем (ортогональные базисы, их веса, минимальные псевдоортогональные числа с их рангами и кратности).

2.         Конструируют число  из минимальных псевдоортогональных чисел , , с рангами , которые однозначно определяются выбранной системой оснований . В результате, получают число , где - след числа, а его ранг находят по теореме о ранге суммы:

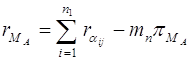, (4.2´)

где  - число переходов по основанию

3.         Расширяют число  по формуле расширения (4.1´). Пользуясь величиной ранга , вычисленной по формуле (4.2´), получают число , которое отличается от искомого числа А цифрами по двум последним основаниям.

4.         Если , то , т. е.  - искомое расширение числа А.

5.         Если , то прибавляют к числу  такое из минимальных псевдоортогональных чисел  кратности , где , которое превратит цифру по основанию  в . В результате, получают число .

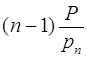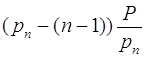6.         Если кратность , то число  является искомым расширением числа А, так как к числу , не превышающему  прибавили число , не превышающее , т. е.  не превышает Р, т. е. величины 1-го интервала.

7.         Если , то число  может располагаться либо в последних 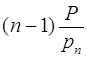 частях 1-го интервала [0; P), либо в младших  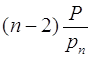частях второго интервала [P; 2P), а тогда искомым является число .

Еще один путь решения поставленной задачи представляет собой перевод числа из СОК в ОПС с дополнительным финальным шагом. Рассмотрим этот метод.

Пусть СОК состоит из оснований , , …, . Объем диапазона этой системы будет 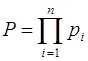. Добавим к числу оснований СОК новое основание . Объем диапазона этой системы 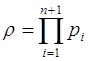. Тогда любое число  из диапазона [0; ) в обобщенной позиционной системе счисления представимо в виде =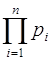++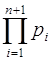…+ ++. Если число  будет лежать в первоначальном диапазоне [0; ), то в ОПС цифра = 0. Этот факт и используется для получения остатка от деления числа  на новое основание СОК .

Пусть число  имело представление (, , …, ) по основаниям , , …, . Добавляем новое основание , тогда число =(, , …, , ) в системе оснований , , …, , , где  – остаток от деления числа  на , т.е. искомая цифра по новому основанию.

Для определения этой цифры рассматриваем алгоритм перевода числа из СОК в ОПС, включая неизвестную цифру  в проводимые операции. При этом мы последовательно будем получать цифры ОПС , , …,  и выражение для цифры . Но так как по предположению число [ 0; ), то цифра = 0. Из полученного соотношения и определяем искомую цифру .

Пример. Пусть задана система модулей = 2, = 3, = 5, = 7, тогда = 2·3·5·7=210. И пусть задано число = 157= (1, 1, 2, 3). Расширим систему оснований, добавляя = 11. Пусть = (1, 1, 2, 3, ) в системе оснований = 2, = 3, = 5, = 7, = 11. Набор констант =  задается матрицей

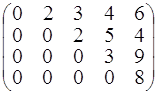
Процесс решения задачи покажем

Расширение оснований модулярного кода

Действия	Модули					Цифры СОК
	2	3	5	7	11
_ х  а1	1 1	1 1	2 1	3 1	1	а1=0
х-а1 ´	0	0 2	1 3	2 4	-1  6
_ х1  а2		0 0	3 0	1 0	6-6  0	а2=0
х1-а2 ´		0	3 2	1 5	6-6  4
_ х2  а3			1 1	5 1	2-2  1	а3=1
х2-а3 ´			0	4 3	2-3  9
_ х3  а4				5 5	7-5  5	А4=5
х3-а4 ´				0	7-10  8
x4					-3	а5=-3

Таким образом, а₅ = – 3, но по условию а₅ = 0, т.е. – 3 = 0, откуда = 3. Получим расширенное представление числа = 157 = (1, 1, 2, 3, 3) по основаниям

= 2, = 3, = 5, = 7, = 11.

Этот алгоритм может быть несколько видоизменен за счет следующего свойства:

.

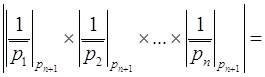
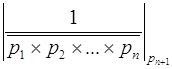Фактически величина 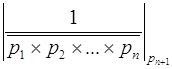 используется только на последнем шаге определения цифры . Поэтому в столбце по новому основанию  с самого начала можно записать ноль и применить алгоритм перевода числа из СОК в ОПС.

Пусть по этому алгоритму будет получено что = для числа (, , …, , 0). Тогда  для числа  можно найти из соотношения:

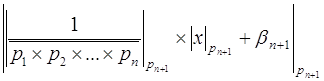= 0.

Рассмотрим на том же примере эту модификацию алгоритма.

 Модифицированный метод расширения оснований модулярного кода

Действия	Модули					Цифры СОК
	2	3	5	7	11
_ х  а1	1 1	1 1	2 1	3 1	0 1	А1=1
х-а1 ´	0	0 2	1 3	2 4	10 6
_ х1  а2		0 0	3 0	1 0	5 0	А2=0
х1-а2 ´		0	3 2	1 5	5 4
_ х2  а3			1 1	5 1	9 1	А3=1
х2-а3 ´			0	4 3	8 9
_ х3  а4				5 5	6 5	А4=5
х3-а4 ´				0	1 8
x4					8

Тогда ,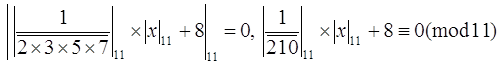

 . Заметим также, что последние умножение на 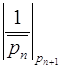 можно не проводить.

Тогда финальный шаг для определения цифры по новому основанию может быть записан как 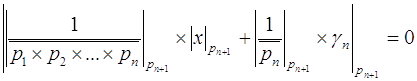, или умножая на , получим 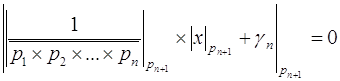, где  - цифра, полученная по основанию  после вычитания цифры . В нашем примере = 1. Таким образом, искомую цифру можно определить из соотношения: 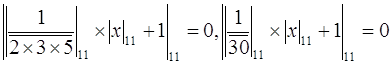, откуда

.

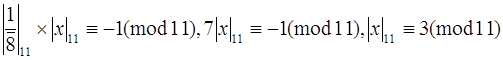Так как результат образования цифры в СОК по новому основанию  зависит только от первых цифр, то операцию расширения можно проводить сразу по нескольким основаниям.

Пример. Пусть задана система оснований

,

 объем диапазона . И пусть задано число  в этой системе оснований.

Найдем расширенное представление этого числа, добавляя модули  и .

Для этого запишем нули в качестве неизвестных цифр и примем вышерассмотренный алгоритм расширения системы оснований.

Константы 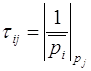 вычислены заранее и записаны в виде матрицы

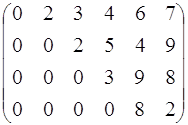
Тогда получаем

Расширение модулярного кода по нескольким основаниям

Действия	Модули						Цифры СОК
_ х  а1	0 0	2 0	2 0	0 0	0 0	0 0	а1=0
х-а1 ´	0	2 2	2 3	0 4	0 6	0 7
_ х1  а2		1 1	1 1	0 1	0 1	0 1	а2=1
х1-а2 ´		0	0 2	6 5	10 4	12 9
_ х2  а3			0 0	2 0	7 0	4 0	а3=0
х2-а3 ´			0	2 3	7 9	4 8
_ х3  а4				6 6	8 6	6 6	а4=6
х3-а4 ´				0	2 8	0 2
x4					5	0

Цифры по основаниям  и  находим из соотношени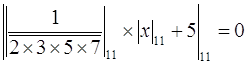й:

 и ,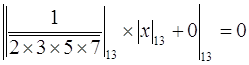

откуда получаем = 6 и = 0.

Таким образом, число  в этой системе оснований

.

Преимущества метода расширения системы основания с помощью перевода в ОПС состоит в том, что:

во-первых, все вычисления идут в параллельных каналах по определенным модулям;

во-вторых, не требуется вычисление большого количества дополнительных величин (необходимо наличие в памяти только констант );

в-третьих, возможно получение расширенного представления числа сразу по нескольким дополнительным основаниям, что не влияет на быстродействие всей операции.

Глава 3. Программная эмуляция алгоритмов перевода чисел из СОК в ПСС и обратно и алгоритма RSA

Программа №1

 

{SN+,E+}{Создание программного кода одинаково пригодного при работе на ПЭВМ с математическим сопроцессором или без него}

program Eyler;

uses crt;

type mas=array[1..20] of longint;

var i,n,b,c,d,v,x,f,f1:longint;

 w:real;

 a,p:mas;

 r:string;

 {Оформление экрана}

 procedure visitka;

 begin

writeln(‘ Министерство образования Российской Федерации ‘);

writeln(‘ Ставропольский государственный университет ‘);

writeln(‘ Кафедра алгебры ‘);

writeln(‘ ‘);

writeln(‘Дипломная работа  ‘);

writeln(‘ ‘);

writeln(‘ Методы перевода чисел из системы остаточных классов‘);

writeln(‘ в позиционную систему счисления ‘);

writeln(‘ ‘);

writeln(‘ Выполнила: Пивоварова Елена Николаевна, ‘);

writeln(‘ФМФ, 5 курс, гр. Б ‘);

writeln(‘Научный руководитель:‘);

writeln(‘заведующая кафедрой алгебры‘);

writeln(‘Копыткова Людмила Борисовна ‘);

writeln(‘‘);

writeln(‘ Нажмите клавишу <Enter> ‘);

writeln(‘ ‘);

writeln(‘Теоретические сведения‘);

writeln(‘ Программа позволяет производить перевод числа‘);

writeln(‘ А=(а₁, а₂, …,а_n), представленного в СОК с основаниями ‘);

writeln(‘ р₁, p₂ ,…,p_n такими, что р₁< p₂ <…<p_n и p(i) – простые ‘);

writeln(‘числа, в позиционную систему счисления методом, ‘);

writeln(‘основанным на применении функции Эйлера. Данный метод‘);

writeln(‘заключается в следующем: для нахождения числа A в‘);

writeln(‘позиционной системе счисления берутся 2 модуля:p(i) и p(i+1),‘);

writeln(‘причем p(i) > p(i+1), и соответствующие им остатки а(i) и а(i+1). ‘);

writeln(‘Находится наименьший неотрицательный вычет по модулю ‘);

writeln(‘p(i) * p(i+1). Применяя эту операцию многократно и переходя ‘);

writeln(‘к составным модулям, осуществляют перевод чисел. ‘)

writeln;writeln;writeln;

 writeln ('Нажмите клавишу <Enter>...');

 readln;

 clrscr;

 end; {visitka}

 {Вычисление наименьшего неотрицательного вычета}

 procedure vich (var v:longint; a,m:longint);

 begin if a<0 then v:=a+m else v:=a mod m

 end;{vich}

 {Тест простого числа}

 function test (ch:longint):boolean;

 var i:longint;

 begin i:=2;

 while (i<=ch) and ((ch mod i)<>0) do

 i:=i+1+(i mod 2);

 if i=ch then test:=true else test:=false;

 end;{test}

 {Ввод данных}

 procedure DataEnter;

 var i:longint;

 begin

 write('Введите число модулей:');

 readln(n);

 writeln('Ввод значения модулей (p(i)<=30, p(i)-простые,');

 writeln('p(i)<p(i+1)):');

 for i:=1 to n do

 begin

 while true do begin

 write('Модуль p',i ,'= ');

 readln(p[i]);

 if (p[i]<=30) and Test(p[i]) then

 begin if i<>1 then begin

 if p[i]>p[i-1] then break;

 end

 else break;

 end;

 end;{while}

 end;{for}

 writeln('Ввод числа в СОК (a(i)>=0 и a(i)<p(i)):');

 for i:=1 to n do

 begin

 while true do begin

 write('a[',i,']=');

 readln(a[i]);

 if (a[i]>=0) and (a[i]<p[i]) then break;

 end;{while}

 end;{for}

 end;{DataEnter}

 {Перевод числа в ПСС}

 procedure Calcx(var x:longint;p,a:mas);

 var i,b,c,f1:longint;

 begin

 f1:=p[2];

 for i:=2 to n do

 begin

 {Вычисление функции Эйлера}

 if p[1]<p[i] then f:=p[i]-1;{f-значение функции Эйлера, если}

 {p[i]-простое число}

 f1:=f1*(p[i]-1);

 if p[1]>p[i] then

 begin b:=p[1];p[1]:=p[i];p[i]:=b;

 c:=a[1];a[1]:=a[i];a[i]:=c;

 f:=f1 {f - значение функции Эйлера, если}

 {f - составное число}

 end;

 {Перевод числа }

 w:=exp((f-1)*ln(p[i]-p[1]));

 vich(d,round(w),p[i]);

 vich(v,a[1]-a[i],p[i]);

 vich(v,d*v,p[i]);

 x:=v*p[1]+a[1];

 p[1]:=p[1]*p[i];

 a[1]:=x;

 end

end;{Calcx}

begin

 repeat

 clrscr;

 visitka;

 dataenter;

 calcx(x,p,a);

 writeln('A= ',x);

 writeln('Повторить? (y/n): ');

 readln(r);

 until (r= 'n')

end.

Министерство образования Российской Федерации

Ставропольский государственный университет

Кафедра алгебры

Дипломная работа

Методы перевода чисел из системы остаточных классов

в позиционную систему счисления

Выполнила:Пивоварова Елена Николаевна,

ФМФ, 5 курс, гр. Б

Научный руководитель:

заведующая кафедрой алгебры

Копыткова Людмила Борисовна

Нажмите клавишу <Enter>

Теоретические сведения

Программа позволяет производить перевод числа

А=(а₁, а₂, …,а_n), представленного в СОК с основаниями

р₁, p₂ ,…,p_n такими, что р₁< p₂ <…<p_n и p(i) – простые

числа, в позиционную систему счисления методом,

основанным на применении функции Эйлера.

Данный метод заключается в следующем:

для нахождения числа A в

позиционной системе счисления берутся 2 модуля:

p(i) и p(i+1), причем p(i) > p(i+1), и

соответствующие им остатки а(i) и а(i+1).

Находится наименьший неотрицательный

вычет по модулю p(i) * p(i+1).

Применяя эту операцию многократно и переходя

к составным модулям, осуществляют перевод чисел.

 

Результаты работы программы

Нажмите клавишу <Enter>…

Введите число модулей:2

Ввод значения модулей (p(i)< =30, p(i)-простые,

p(i)< p(i+1)):

Модуль р1=17

Модуль р2=19

Ввод числа в СОК (а(i)>=0 и (а(i)<p(i)):

a[1]=2

a[2]=3

A=155

Повторить? (у/n):

y

Введите число модулей:3

Ввод значения модулей (p(i)< =30, p(i)-простые,

p(i)< p(i+1)):

Модуль р1=2

Модуль р2=3

Модуль р3=5

Ввод числа в СОК (а(i)>=0 и (а(i)<p(i)):

a[1]=1

a[2]=2

a[3]=4

A=29

Повторить? (у/n):

n

Программа №2

program COK_Poliandr;

type mas1=array [1..10] of integer;

 mas2= array [1..10,1..10] of integer;

var p, a, o: mas1;

 t: mas2;

 Aonc, PP, i, j, y, k, n, f : integer;

begin

writeln ('Перевод чисел из СОК в обобщенную систему счисления ');

write ('Введите размер системы оснований = ');

readln (n);

writeln ('Введите каждое основание ');

PP:=1;{Присвоение начального значения объему диапазона}

for i:=1 to n do begin {Ввод системы оснований и вычисление объёма

 диапазона}

 write ('p[',i,']= ');

 readln (p[i]);

 PP:=PP*p[i];

 end;

writeln ('Объем диапазона Р =',PP);

writeln ('Введите число в СОК по цифрам: ');

for i:=1 to n do begin{Ввод исходного числа в СОК}

 write (i,' цифра = ');

 readln (a[i]);

 end;

write('Переведём число А = ( '); {Вывод на экран исходного числа}

for i:=1 to n do write (a[i],',');

writeln(') в ОПС.');

writeln ('На первом этапе получим матрицу констант ');

for k:=1 to n do

for J:=k to n do{Вычисление матрицы обратных элементов по

умножению для чисел p_k по модулю p_j}

begini:=0; f:=0;

 repeat if (1+i*p[j]) mod p[k] =0 then begin

t[k,j]:=(1+i*p[j]) div p[k];f:=1;{Флаг поднят, если произошло вычисление константы}

end;

 i:=i+1;

 until (i>n) or (f=1);{Выход из цикла, если поднят флаг или превышено значение параметра}

end;

for k:=1 to n do begin{Вывод полученной матрицы}

for J:=1 to n do write(t[k,j],' ');

writeln;

 end;

write ('Затем получим цифры ОПС: ');

for j:=1 to n do begin o[j]:=a[j];{Получение очередной цифры}

for i:=j to n do begin

 if a[i]>=o[j] then a[i]:=a[i]-o[j] {Первое действие}

 else a[i]:=a[i]+p[i]-o[j];

 a[i]:=a[i]*t[j,i]; {Второе действие}

 if a[i]>p[i] then a[i]:=a[i] mod p[i];

 end;

write(o[j],' ');{Вывод очередной цифры ОПС}

 end;

writeln;

write ('В итоге, получим число: ');

Aonc:=0; y:=1;{Обнуление результата}

for i:=1 to n do begin{Получение числа в позиционной системе счисления по его цифрам }

Aonc:= Aonc+y*o[i];

y:=y*p[i];

 end;

writeln (Aonc);{Вывод полученного результата}

readln;{Задержка результата на экране

до нажатия клавиши ENTER}

end.

Результаты работы программы

Перевод чисел из СОК в обобщенную систему счисленияВведите размер системы оснований = 5

Введите каждое основание

p[1]=2

p[2]=3

p[3]=5

p[4]=7

p[5]=11

Объем диапазона Р =2310

Введите число в СОК по цифрам: 1 цифра = 1

2 цифра = 2

3 цифра = 1

4 цифра = 4

5 цифра = 7Переведём число А = ( 1, 2, 1, 4, 7,) в ОПС.

На первом этапе получим матрицу констант 0 0 2 3 4 5

0 0 0 2 5 4

0 0 0 0 3 9

0 0 0 0 0 8

0 0 0 0 0 0

Затем получим цифры ОПС: 1 2 1 0 7

В итоге, получим число: 1481

Применение СОК не ограничивается только переводом чисел из СОК в ПСС и обратно. Например, ещё СОК можно использовать для шифровки сообщений.

Программа №3

В данной программе реализуется шифрование и расшифрование сообщения методом RSA.

Блок-схема алгоритма нахождения А^-1 mod N

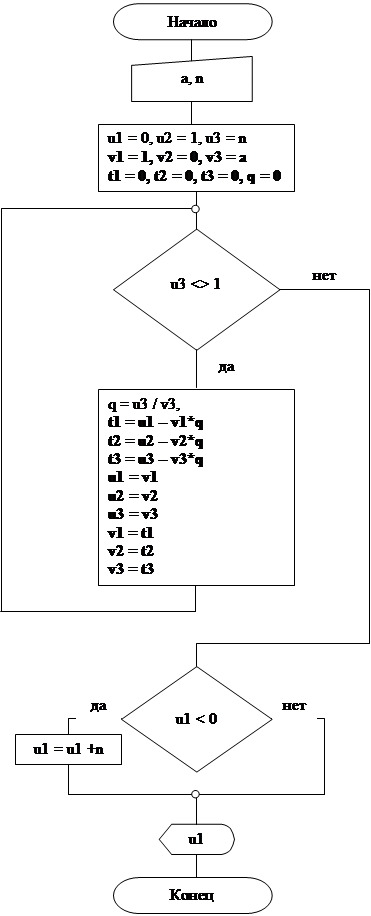
Блок-схема алгоритма вычисления a^d (mod N)

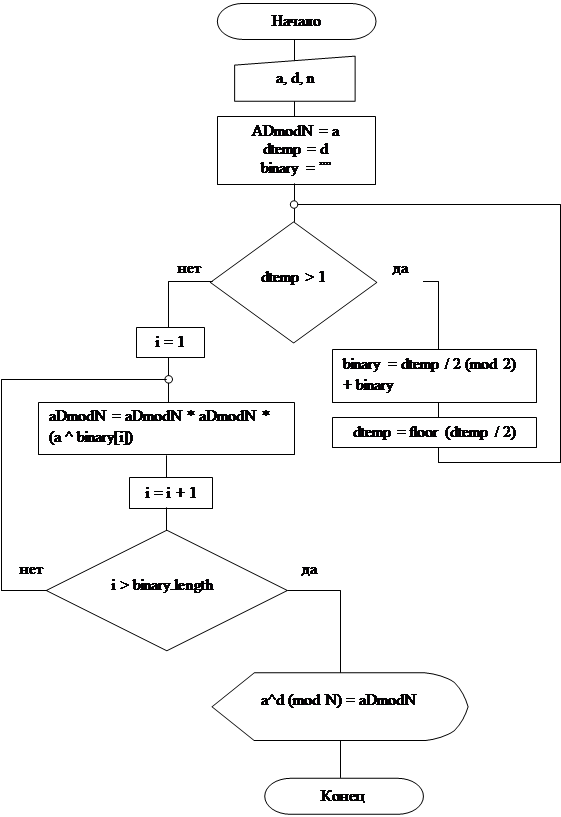
Блок-схема алгоритма нахождения простых чисел не превышающих N

 

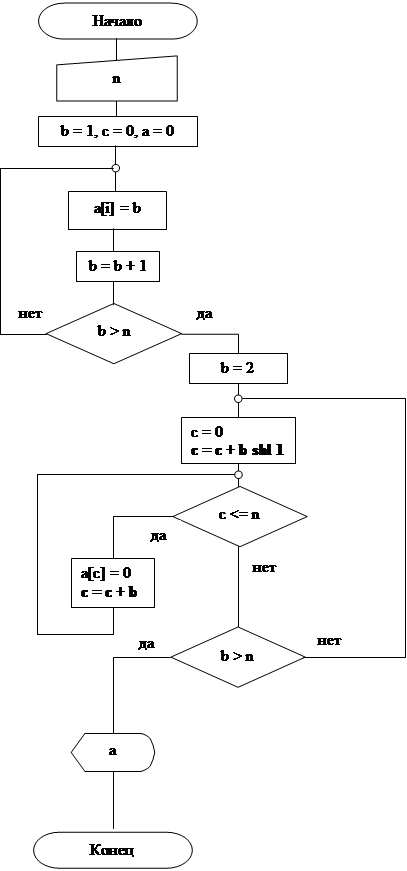
Блок-схема реализации алгоритма RSA

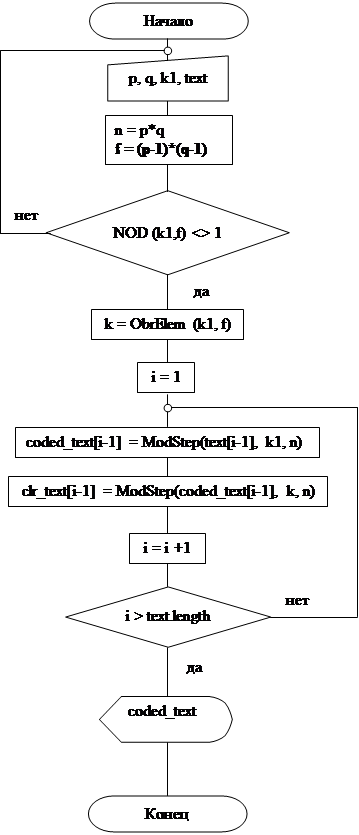
Листинг программы

#include <vcl.h>

#pragma hdrstop

#include "Unit1.h"

#include <math.h>

#pragma package(smart_init)

#pragma resource "*.dfm"

using namespace std;

TForm1 *Form1;

__fastcall TForm1::TForm1(TComponent* Owner)

 : TForm(Owner)

{

}

void __fastcall TForm1::Button2Click(TObject *Sender)

{

 Close();

}

void __fastcall TForm1::Button1Click(TObject *Sender)

{

 Log->Lines->Clear();

 srand( GetTickCount() );

// Ввод P и Q

 

 int p = StrToInt( Edit1->Text );

 int q = StrToInt( Edit2->Text );

 Log->Lines->Add( "p = " + IntToStr( p ) );

 Log->Lines->Add( "q = " + IntToStr( q ) );

// Вычисление N

 int N = p * q;

 Log->Lines->Add( "N = p*q = " + IntToStr( N ) );

// Вычисление f(N)

 int f = (p-1)*(q-1);

 Log->Lines->Add( "f(n)=(p-1)(q-1) = " + IntToStr( f ) );

// Ввод открытого ключа K1

 int k1 = StrToInt( edtOK->Text );

 Log->Lines->Add( "k1 = " + IntToStr( k1 ) );

// Проверка условий существования открытого ключа

 if( NOD( k1, f ) != 1 )

 {

 Log->Lines->Add( "открытый ключ и f(n) не взаимно простые. введите новые параметры" );

 return;

 }

// Нахождение секретного ключа

 int k = ObrElem( k1, f );

 Log->Lines->Add( "k = k1^(-1) mod f(n) = " + IntToStr( k ) );

 AnsiString clear = Edit3->Text;

 AnsiString coded;

// Шифрование и расшифрование сообщения

 coded = "";

 int *clear_c = new int[clear.Length()];

 int *coded_c = new int[clear.Length()];

 int *clr_c = new int[clear.Length()];

 for( int i = 1; i <= clear.Length(); i++ )

 {

 clear_c[i-1] = (int)clear[i];

 coded_c[i-1] = ModStep( clear_c[i-1], k1, N );

 clr_c[i-1] = ModStep( coded_c[i-1], k, N );

 char temp[256];

 wsprintf( temp, "%c = %c = %c", clear[i], (char)coded_c[i-1], (char)clr_c[i-1] );

 Log->Lines->Add( temp );

 wsprintf( temp, "%c", (char)coded_c[i-1] );

 coded += temp;

 }

 delete[] clr_c;

 delete[] coded_c;

 delete[] clear_c;

// Вывод полученных результатов

 Log->Lines->Add( "clear text = " + clear );

 Log->Lines->Add( "coded text = " + coded );

 Log->Lines->Add( "" );

}

// Модуль нохождения НОД (a, b)

int __fastcall TForm1::NOD(int a, int b)

{

if( ( a == 0 )||( b == 0 ) )

 {

return abs( a + b );

}

 while( a != b )

{

 if( a > b )

{

a -= b;

}

else

{

b -= a;

}

}

 return b;

}

//Модуль нахождения обратного элемента по модулю N

int __fastcall TForm1::ObrElem(int a, int N)

{

int u1 = 0, u2 = 1, u3 = N;

int v1 = 1, v2 = 0, v3 = a;

int t1, t2, t3, q;

while(u3 != 1)

{

q = u3 / v3;

t1 = u1 - v1*q;

t2 = u2 - v2*q;

t3 = u3 - v3*q;

u1 = v1;

u2 = v2;

u3 = v3;

v1 = t1;

v2 = t2;

v3 = t3;

}

 return u1 < 0 ? u1 + N : u1;

}

// Модуль возведения числа в степень по модулю N

int __fastcall TForm1::ModStep(int a, int d, int n)

{

 int aBmodN = a;

 int dtemp = d;

 AnsiString binary = "";

 while( dtemp > 1 )

 {

 binary += IntToStr( dtemp % 2 );

 dtemp = floor( dtemp / 2 );

 }

 binary += dtemp;

 for( int i = 1; i < binary.Length(); i++ )

 {

 aBmodN = aBmodN*aBmodN * ( binary[binary.Length() - i] == '0' ? 1 : a ) % n;

 }

 return aBmodN;

}

void __fastcall TForm1::Button3Click(TObject *Sender)

{

 int q = 0;

 int p = 0;

 int *a = new int[256];

 prost( a, 64 );

 srand( GetTickCount() );

 while( ( p == 0 )||( p > 64 ) )

 {

 p = a[ rand() % 64-1 ];

 }

 while( ( q == 0 )||( q > 64 ) )

 {

 q = a[ rand() % 64-1 ];

 }

 Edit1->Text = FloatToStr( p );

 Edit2->Text = FloatToStr( q );

 delete[] a;

}

// Модуль нахождения простых чисел на превышающих N методом решета Эратосфера

void __fastcall TForm1::prost( int *a, int n )

{

int b, c;

 for( b = 1; b <= n; b++ )

{

 a[b] = b;

}

 for( b = 2; b <= floor( sqrt( n ) ); b++ )

{

 c = 0;

 c += ( b << 1 );

 while( c <= n )

 {

 a[c] = 0;

 c += b;

 }

 }

}

Цитированная литература

1.  Бухштаб А. А. Теория чисел – М: Наука, 1975 г.

2.  Айерленд К. Классическое введение в современную теорию чисел. М: Мир, 1987.

3.   Акушинский И. Л., Юдицкий Д. И. Машинная арифметика в остаточных классах. – М. Советское радио, 1968.

4.  Амербаев В. М. Теоретические основы мащинной арифметики, - Алма –Ата: Наука, 1976.

5.  Червяков Н. И. Применение нейронных сетей для прямого и обратного преобразования кодов в СОК. Вестник СГУ, Физ.-мат. науки, 1999.

6.  Червяков Н. И. Применение системы остаточных классов в цифровых системах обработки и передачи информации. – Ставрополь: СВВиУС, 1984.

7.  Червяков Н. И. Преобразование цифровых позиционных и непозиционных кодов в системах управления и связи. – Ставрополь: СВВиУС, 1985.

8.  Коляда А. А., Пак И. Т. Модулярные структуры конвейерной обработки цифровой информации, - Минск: Университетское, 1992.

9.  Онищенко С. М. Применение гиперкомплексных чисел в теории инерциальной навигации. Автономные системы, - Киев: Наукова думка, 1983.