Связный ориентированный граф G (Х, Г) задан множеством вершин X={x1, x2, …, xn} и отображением Гxi={x|I±k|, x|I±l|}, i =1, 2,…, n. Здесь i - текущий номер вершины, n- количество вершин графа. Значение индексов n, k и l возьмем из табл.1 в соответствии с номером варианта. Индексы k и l формируют значения индексов a, b , g… переменной x в отображении Гxi = {xa, xb, xg,…}. Если значения индексов a, b, g… переменной x не соответствуют ни одному из номеров вершин графа, то эта переменная не учитывается во множестве Гxi.
Выполнить следующие действия:
а) определить исходный граф и ассоциированный с ним неориентированный граф графическим, матричным и аналитическим способами;
б) установить центры и периферийные вершины графов, найти радиусы и диаметры графов;
в) выделить в ориентированном графе два подграфа. Найти объединение, пересечение и разность подграфов;
г) описать систему уравнений, соответствующую сигнальному графу, считая, что передача между вершинами xi и xj
![]() i*j при i ³ j;
i*j при i ³ j;
Kij =
1/ (p+1) при i<j .
Найти передачу между вершинами x1и xn, используя правило Мезона. Построить структуру кибернетической системы, определяемой топологией графа;
Таблица 1
| № варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| N | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | 6 | 6 |
| K | 2 | 3 | 4 | 1 | 1 | 1 | 3 | 5 | 2 | 4 | 2 | 3 | 4 | 5 | 6 |
| L | 1 | 1 | 1 | 2 | 3 | 4 | 2 | 1 | 3 | 3 | 1 | 1 | 1 | 1 | 1 |
| № варианта | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| N | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 7 | 7 |
| K | 1 | 1 | 1 | 1 | 3 | 2 | 5 | 5 | 2 | 3 | 4 | 5 | 6 | 5 | 3 |
| L | 2 | 3 | 4 | 5 | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 2 | 1 | 3 | 5 |
Решение:
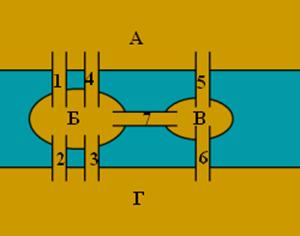
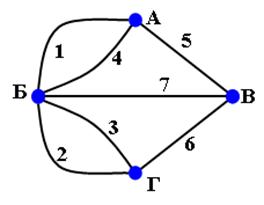
Множество вершин
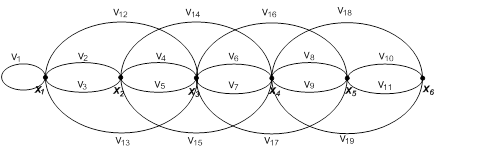
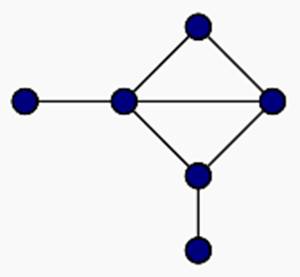
X = {x1, x2, x3, x4, x5, x6 }, n = 6 k = 2, l = 1 Гxi={x|I±k|, x|I±l|}.
а) определим исходный граф и ассоциированный с ним неориентированный граф графическим, матричным и аналитическим способами:
Определим граф аналитическим способом:
Гx1 = { x1, x3, x2 };
Гx2 = { x4, x1, x3 };
Гx3 = { x1, x5, x2, x4 };
Гx4 = { x2, x6, x3, x5 };
Гx5 = { x3, x4, x6 };
Гx6 = {x4, x5 }.
Ориентированный граф графическим способом:
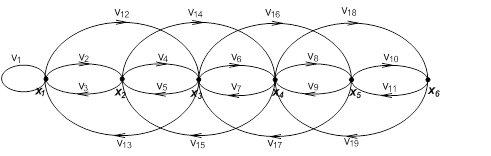
Неориентированный граф графическим способом:
Ориентированный граф матричным способом:
RG - матрица смежности 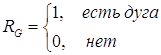
| x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | 1* | 1 | 1 | 0 | 0 | 0 |
| x2 | 1 | 0 | 1 | 1 | 0 | 0 |
| x3 | 1 | 1 | 0 | 1 | 1 | 0 |
| x4 | 0 | 1 | 1 | 0 | 1 | 1 |
| x5 | 0 | 0 | 1 | 1 | 0 | 1 |
| x6 | 0 | 0 | 0 | 1 | 1 | 0 |
AG - матрица инцидентности 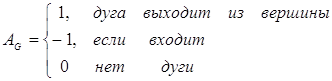
| v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 | v10 | v11 | v12 | v13 | v14 | v15 | v16 | v17 | v18 | v19 | |
| x1 | 1* | 1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 |
| x2 | 0 | -1 | 1 | 1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | -1 | 0 | 0 | 0 | 0 |
| x3 | 0 | 0 | 0 | -1 | 1 | 1 | -1 | 0 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 1 | -1 | 0 | 0 |
| x4 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | -1 | 0 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 1 | -1 |
| x5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | -1 | 0 | 0 | 0 | 0 | -1 | 1 | 0 | 0 |
| x6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 |
Неориентированный граф матричным способом:
RD - матрица смежности
| x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | 1* | 2 | 2 | 0 | 0 | 0 |
| x2 | 2 | 0 | 2 | 2 | 0 | 0 |
| x3 | 2 | 2 | 0 | 2 | 2 | 0 |
| x4 | 0 | 2 | 2 | 0 | 2 | 2 |
| x5 | 0 | 0 | 2 | 2 | 0 | 2 |
| x6 | 0 | 0 | 0 | 2 | 2 | 0 |
AD - матрица инцидентности
| v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 | v10 | v11 | v12 | v13 | v14 | v15 | v16 | v17 | v18 | v19 | |
| x1 | 1* | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| x2 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| x3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| x4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| x6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
б) установить центры и периферийные вершины графов, найти радиусы и диаметры графов:
![]() - матрица отклонений имеет вид:
- матрица отклонений имеет вид:
| x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | 1 | 1 | 1 | 2 | 2 | 3 |
| x2 | 1 | 0 | 1 | 1 | 2 | 2 |
| x3 | 1 | 1 | 0 | 1 | 1 | 2 |
| x4 | 2 | 1 | 1 | 0 | 1 | 1 |
| x5 | 2 | 2 | 1 | 1 | 0 | 1 |
| x6 | 3 | 2 | 2 | 1 | 1 | 0 |
![]() - вектор отклонения
- вектор отклонения
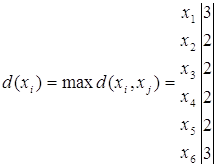 =>
=>
х2, х3, х4, х5 - центры графа с наименьшей удаленностью. Радиус ρ (G) = 2.
Периферийными вершинами являются вершины х1, х6с наибольшей удаленностью. Диаметр графа D (G) = 3.
в) выделим в ориентированном графе два подграфа и найдем объединение, пересечение и разность подграфов.


Выделяем два подграфа: G1 и G2
X1 - {x1, x2}, Г1х1 = {x1, x2}, Г1х2 = {x1},
X2 - {x1, x2,x3}, Г2х1 = {x2}, Г2х2 = {x3}, Г2х3 = {x2}.
Объединение ![]() ,
,
![]() ,
,![]() ,
, ![]() ,
, ![]() .
.
G 
Пересечение
![]() ,
,![]() ,
,![]() ,
, ![]() .
.
G 
Разность
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
G 
г) Считая, что передача между вершинами xi и xj
![]() i*j при i ³ j;
i*j при i ³ j;
Kij =
1/ (p+1) при i<j .
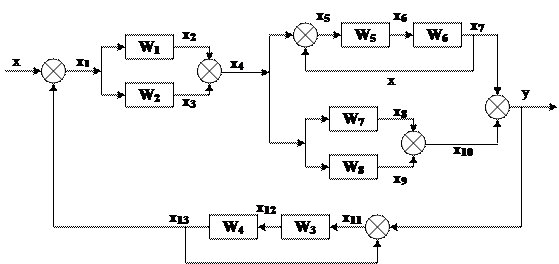
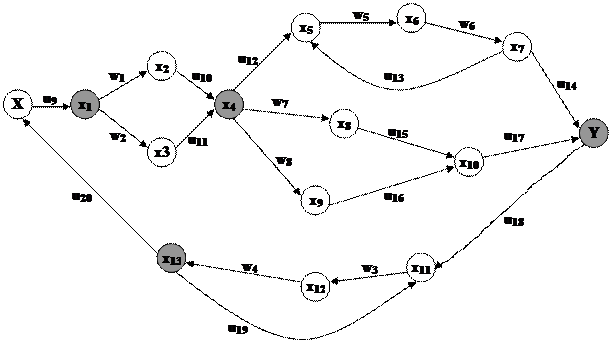
Сигнальный граф имеет вид
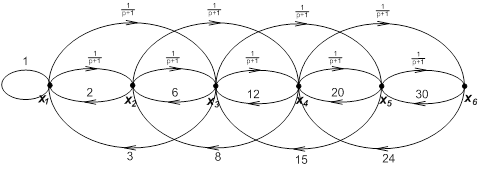
Система уравнений, соответствующая сигнальному графу имеет вид
x1 = x1 +2x2 +3x3
x2 =![]() x1 +6 x3 +8 x4
x1 +6 x3 +8 x4
x3 =![]() x1 +
x1 +![]() x2+12x4 +15x5
x2+12x4 +15x5
x4 = ![]() x2 +
x2 +![]() x3 +20 x5 +24x6
x3 +20 x5 +24x6
x5 = ![]() x3 +
x3 +![]() x4 +30x6
x4 +30x6
x6 =![]() x4 +
x4 +![]() x5
x5
Определить передачу k16 по правилу Мезона. Формула Мезона имеет вид
![]()
PS - передача пути,
DS - алгебраическое дополнение,
D - определитель.
![]()
Пути из х1 в х6 и передаточные функции для каждого из них имеют вид:
![]()
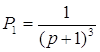
![]()
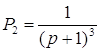
![]()
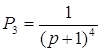
![]()
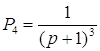
![]()
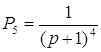
![]()
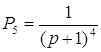
Контура:
![]() ;
;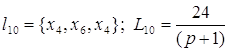
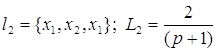 ;
;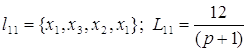 ;
;
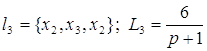 ;
;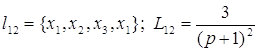 ;
;
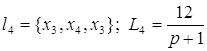 ;
;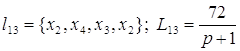 ;
;
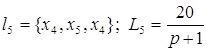 ;
;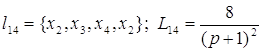 ;
;
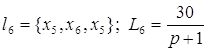 ;
;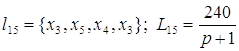 ;
;
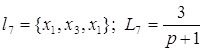 ;
;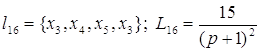
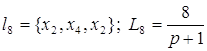 ;
;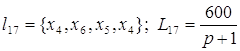 .
.
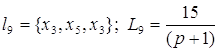 ;
;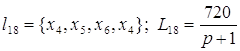 .
.
Пары несоприкасающихся контуров
L1L3, L1L4, L1L5, L1L6, L1L8, L1L9, L1L10, L1L13, L1L14, L1L15, L1L16, L1L17, L1L18;
L2L4, L2L5, L2L6, L2L8, L2L9, L2L10, L2L15, L2L16, L2L17, L2L18;
L3L5, L3L6, L3L10, L3L17, L3L18;
L4L6, L5L7; L5L11, L5L12, L6L7, L6L8, L6L11, L6L12, L6L13, L6L14;
L7L8, L7L10, L7L17, L7L18;
L8L9, L9L10, L10L11, L10L12, L11L17, L11L18, L12L17, L12L18.
Независимые тройки
L1L3L5,L1L3L6,L1L3L10,L1L3L17,L1L3L18,L1L4L6,L1L6L8,L1L6L13,L1L6L14,L1L8L9,L1L9L10,L2L4L6,L2L9L10,L6L7L8.
Отсюда
D = 1 - (L1 +L2 +L3 +L4 +L5 + L6 +L7 + L8 +L9 +L10 +L11 +L12 +
+L13 +L14+L15 +L16+L17 +L18)+ (L1L3+L1L4+L1L5+L1L6+L1L8+L1L9+L1L10+L1L13+L1L14+L1L15+L1L16+L1L17+L1L18+L2L4+L2L5+L2L6+L2L8+L2L9+L2L10+L2L15+L2L16+L2L17+L2L18 +L3L5+L3L6+L3L10+L3L17+L3L18 L4L6+L5L7+L5L11+L5L12+L6L7+L6L8+L6L11+L6L12+L6L13+L6L14+L7L8+L7L10+L7L17+L7L18+L8L9+L9L10+L10L11+L10L12+L11L17+L11L18+L12L17+L12L18) -
(L1L3L5+L1L3L6+L1L3L10+L1L3L17+L1L3L18+L1L4L6+L1L6L8+L1L6L13+L1L6L14+L1L8L9+L1L9L10+L2L4L6+L2L9L10+L6L7L8).
D1 = 1- L8;
D2 = 1;
D3 = 1;
D4 = 1 - L9;
D5 = 1;
D6 = 1.
![]() .
.
Структура кинематической системы представлена на рисунке:
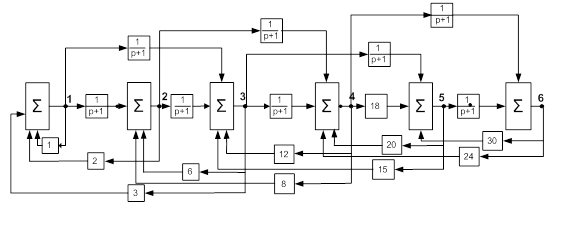
Задача 2. Задача о максимальном потоке и потоке минимальной стоимости
Транспортная сеть задана в виде ориентированного графа, приведенного на рисунке.
На каждом из ребер проставлены значения пропускной способности С (n) ребра n.
Для заданной сети определить максимальный поток jmax транспортировки груза между указанной парой вершин, считая одну из них источником, а другую — стоком.
Решение:
Максимальный поток jmax транспортировки груза между указанной парой вершин, считая одну из них источником, а другую — стоком:
Первый шаг.1. Находим какой-либо путь из х1 в х9 с положительной пропускной способностью.
Tаблица 1.
| x1 | x2 (1) | x3 (1) | x4 (1) | x5 (2) | x6 (3) | x7 (3) | x8 (2) | x9 (6) | |
| x1 | 7 | 9- | 4 | ||||||
| x2 | 0 | 8 | 3 | 6 | |||||
| x3 | 0+ | 5 | 8- | 4 | |||||
| x4 | 0 | 0 | 0 | 9 | 2 | ||||
| x5 | 0 | 2 | |||||||
| x6 | 0+ | 5 | 3- | ||||||
| x7 | 0 | 0 | 0 | 7 | 6 | ||||
| x8 | 0 | 0 | 0 | 0 | 8 | ||||
| x9 | 0+ | 0 | 0 |
В результате получен путь l1 = (x1, х3, х6, х9). Элементы этого пути Cij помечаем знаком минус, а симметричные элементы Cji - знаком плюс.
Определяем пропускную способность найденного пути, которая равна наименьшей из пропускных способностей дуг:
![]()
Определяем остаточные пропускные способности дуг найденного пути и симметричных ему дуг. Для этого из элементов ![]() табл.1 вычитаем C1, а к элементам
табл.1 вычитаем C1, а к элементам ![]() прибавляем C1. В результате получим новую табл.2 с измененными пропускными способностями.
прибавляем C1. В результате получим новую табл.2 с измененными пропускными способностями.
Tаблица 2
| x1 | x2 (1) | x3 (1) | x4 (1) | x5 (2) | x6 (3) | x7 (3) | x8 (2) | x9 (7) | |
| x1 | 7 | 6- | 4 | ||||||
| x2 | 0 | 8 | 3 | 6 | |||||
| x3 | 3+ | 5 | 5 | 4- | |||||
| x4 | 0 | 0 | 0 | 9 | 2 | ||||
| x5 | 0 | 2 | |||||||
| x6 | 3 | 5 | 0 | ||||||
| x7 | 0+ | 0 | 0 | 7 | 6- | ||||
| x8 | 0 | 0 | 0 | 0 | 8 | ||||
| x9 | 3 | 0+ | 0 |
Второй шаг.1. Помечаем столбцы табл.2, находим второй путь l2 = (x1,x3, х7, х9) и расставляем знаки.
2. Пропускная способность пути l2
![]()
Изменим пропускные способности помеченных дуг на С2 в табл.3.
Tаблица 3
| x1 | x2 (1) | x3 (1) | x4 (1) | x5 (2) | x6 (3) | x7 (4) | x8 (2) | x9 (7) | |
| x1 | 7 | 2 | 4- | ||||||
| x2 | 0 | 8 | 3 | 6 | |||||
| x3 | 7 | 5 | 5 | 0 | |||||
| x4 | 0+ | 0 | 0 | 9- | 2 | ||||
| x5 | 0 | 2 | |||||||
| x6 | 3 | 5 | 0 | ||||||
| x7 | 4 | 0+ | 0 | 7 | 2- | ||||
| x8 | 0 | 0 | 0 | 0 | 8 | ||||
| x9 | 3 | 4+ | 0 |
Третий шаг.1. Пометив столбцы, находим l3 = (x1, х4, х7,x9).
Величина потока по пути l3
![]()
Вычислив новые пропускные способности дуг, приходим к табл.4.
Таблица 4
| x1 | x2 (1) | x3 (1) | x4 (1) | x5 (2) | x6 (3) | x7 (4) | x8 (2) | x9 (8) | |
| x1 | 7- | 2 | 2 | ||||||
| x2 | 0+ | 8 | 3 | 6- | |||||
| x3 | 7 | 5 | 5 | 0 | |||||
| x4 | 2 | 0 | 0 | 7 | 2 | ||||
| x5 | 0 | 2 | |||||||
| x6 | 3 | 5 | 0 | ||||||
| x7 | 4 | 2 | 0 | 7 | 0 | ||||
| x8 | 0+ | 0 | 0 | 0 | 8- | ||||
| x9 | 3 | 6 | 0+ |
Четвертый шаг.1. Помечаем столбцы табл.4, находим четвертый путь l4 = (x1, х2, х8, х9) и расставляем знаки.
2. Пропускная способность пути l4
![]()
Изменим пропускные способности помеченных дуг на С4 в табл.5.
Таблица 5
| x1 | x2 (1) | x3 (1) | x4 (1) | x5 (2) | x6 (3) | x7 (4) | x8 (4) | x9 (8) | |
| x1 | 1 | 2 | 2- | ||||||
| x2 | 6 | 8 | 3 | 0 | |||||
| x3 | 7 | 5 | 5 | 0 | |||||
| x4 | 2+ | 0 | 0 | 7 | 2- | ||||
| x5 | 0 | 2 | |||||||
| x6 | 3 | 5 | 0 | ||||||
| x7 | 4 | 2 | 0 | 7 | 0 | ||||
| x8 | 6 | 0+ | 0 | 0 | 2- | ||||
| x9 | 3 | 6 | 6+ |
Пятый шаг.1. Помечаем столбцы табл.5, находим четвертый путь l5 = (x1, х4, х8, х9) и расставляем знаки.
2. Пропускная способность пути l5
![]()
Изменим пропускные способности помеченных дуг на С5 в табл.6.
Таблица 6
| x1 | x2 (1) | x3 (1) | x4 (1) | x5 (2) | x6 (3) | x7 (4) | x8 (5) | x9 | |
| x1 | 1 | 2 | 0 | ||||||
| x2 | 6 | 8 | 3 | 0 | |||||
| x3 | 7 | 5 | 5 | 0 | |||||
| x4 | 4 | 0 | 0 | 7 | 0 | ||||
| x5 | 0 | 2 | |||||||
| x6 | 3 | 5 | 0 | ||||||
| x7 | 4 | 2 | 0 | 7 | 0 | ||||
| x8 | 6 | 2 | 0 | 0 | 0 | ||||
| x9 | 3 | 6 | 8 |
Шестой шаг. Просматривая строки и помечая столбцы, убеждаемся в том, больше не существует ни одного пути с положительной пропускной способностью из вершины x1 в вершину x9. Подмножество R образуют помеченные вершины х1,х2, х3, х4, х5, х6, х7,х8, а подмножество ![]() - одна непомеченная вершины х9. Разрез с минимальной пропускной способностью образуют дуги, начальные вершины которых принадлежат подмножеству R, а конечные -
- одна непомеченная вершины х9. Разрез с минимальной пропускной способностью образуют дуги, начальные вершины которых принадлежат подмножеству R, а конечные - ![]() . Таким образом, разрез с минимальной пропускной способностью
. Таким образом, разрез с минимальной пропускной способностью ![]() . Удалив дуги этого разреза, блокируем все пути из источника в сток. Пропускная способность разреза
. Удалив дуги этого разреза, блокируем все пути из источника в сток. Пропускная способность разреза
![]()
Заключительный шаг. Вычитая из элементов табл.1 соответствующие элементы табл.6, получим табл.7
Таблица 7.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | |
| x1 | 6 | 7 | 4 | ||||||
| x2 | -6 | 0 | 0 | 6 | |||||
| x3 | -7 | 0 | 3 | 4 | |||||
| x4 | -4 | 0 | 0 | 2 | 2 | ||||
| x5 | 0 | 0 | |||||||
| x6 | -3 | 0 | 3 | ||||||
| x7 | 4 | 2 | 0 | 0 | 6 | ||||
| x8 | -6 | -2 | 0 | 0 | 8 | ||||
| x9 | -3 | -6 | -8 |
Величина максимального потока равна сумме элементов x1-й строки табл.7 или сумме элементов x9-го столбца.
Максимальный поток равен ![]() .
.
Сеть Петри задана графически (рис.23…30). В табл.1 в соответствии с вариантом и указанным номером рисунка приведены различные начальные маркировки сети.
Выполнить следующие действия:
Описать сеть аналитическим и матричным способами.
Проверить условия срабатывания каждого из переходов и найти новые маркировки, к которым приведет срабатывание соответствующих переходов, путем выполнения матричных преобразований.
Построить дерево достижимости заданной сети.
Проверить, является ли достижимой одна из маркировок, получаемых на четвертом шаге построения дерева, составив и решив матричные уравнения.
Таблица 1
| № варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| m1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 2 | 2 | 0 | 1 | 3 | 0 | 1 | 1 |
| m2 | 1 | 2 | 2 | 2 | 3 | 1 | 2 | 2 | 1 | 2 | 3 | 1 | 1 | 2 | 0 |
| m3 | 2 | 3 | 1 | 0 | 1 | 1 | 1 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 3 |
| m4 | 3 | 1 | 3 | 4 | 0 | 2 | 1 | 1 | 0 | 1 | 1 | 2 | 1 | 1 | 2 |
| m5 | 1 | 2 | 5 | 1 | 2 | 2 | 3 | 0 | 3 | 3 | 2 | 0 | 3 | 2 | 1 |
| № рисунка | Рис.23 | Рис.27 | Рис.28 | Рис.29 | |||||||||||
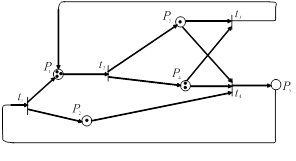
Решение:
Опишем сеть аналитическим и матричным способами. Приведем графическое представление сети Петри, в которой позиции P = {p1, p2, p3, p4, p5} и переходы T = {t1, t2, t3 , t4 }.
Начальная маркировка сети обозначается вектором μ0 [μ1,μ2,μ3,μ4,μ5], μ0 [1 3 0 1 2]. Отсюда получим:
При аналитическом способе задания сеть Петри задается как C = (P,T,F,H,μ0), где, кроме множеств позиций Р и переходов Т, задаются входная F и выходная Н функции.
Через F (tj) обозначается множество входных позиций, а через H (tj) - множество выходных позиций перехода tj; μ0 - начальная маркировка сети.
F (t1) = {p5},H (t1) = {p1,p2 },
F (t2) = {p1},H (t2) = {p3, p4},
F (t3) = {p3, p4}H (t3) = {p1 },
F (t4) = {p2, p3, p4}H (t4) = {p5 }.
μ0 [1 3 0 1 2]
Матричная форма определения сети Петри эквивалентна аналитическому способу задания C = (P,T,D-,D+,μ0). Здесь D- и D+ - матрицы входных и выходных инциденций соответственно размером m × n, где m - число переходов и n - число позиций.
Элемент dij- матрицы D- равен кратности дуг, входящих в i-й переход из j-й позиции.
Элемент dij+ матрицы D+ равен кратности дуг, выходящих из i-ro перехода в j-ю позицию.
Для рассматриваемой сети Петри
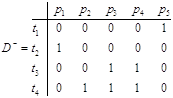
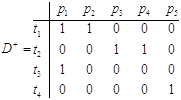
![]()
![]()
Матрица D = D+ - D - называется матрицей инцидентности сети Петри,
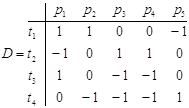
2. При начальной маркировке μ0 [1 3 0 1 2] сети Петри разрешенными являются переходы t1 и t2.
Условия срабатывания для перехода t3 и t4 не выполняется.
Переход t1
[μ0] ≥ [1000]* D- = [1000] · 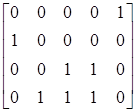 ; [1 3 0 1 2] ≥ [00001] –
; [1 3 0 1 2] ≥ [00001] –
условие выполняется, переход разрешен.
Новая маркировка при срабатывании перехода t1 равна:
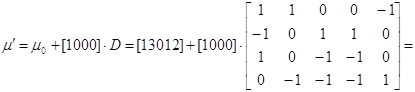
![]() .
.
Переход t2
[μ0] ≥ [0100]* D- = [0100] 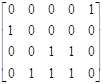 ·;[1 3 0 1 2] ≥ [10000] –
·;[1 3 0 1 2] ≥ [10000] –
условие выполняется, переход разрешен.
Новая маркировка при срабатывании перехода t2 равна:
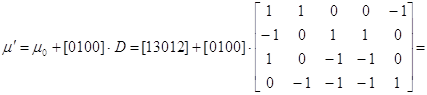
![]() .
.
Переход t3
[μ0] ≥ [0010]* D- = [0010] 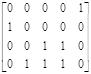 ·;[1 3 0 1 2] ≥ [00110] - условие не
·;[1 3 0 1 2] ≥ [00110] - условие не
выполняется, переход запрещен.
Переход t4
[μ0] ≥ [0001]* D- = [0001] 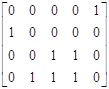 ·;[1 3 0 1 2] ≥ [01110] –
·;[1 3 0 1 2] ≥ [01110] –
условие не выполняется, переход запрещен.
Построим дерево достижимости заданной сети.
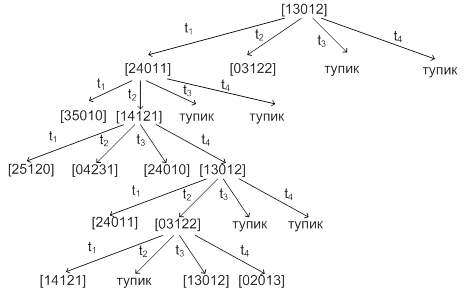
Проверим, является ли достижимой одна из маркировок, полученных на пятом шаге построения дерева, составив и решив матричные уравнения.
Уравнение ![]() принимает вид
принимает вид
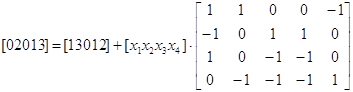
Перенесем ![]() в левую часть и выполним умножение, тогда
в левую часть и выполним умножение, тогда
![]() .
.
Приравняем составляющие векторов
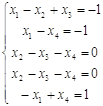
Система имеет решение x1 = 1; x2 = 2; x3 = 0; x4 = 2.
Это значит, что исследуемая маркировка достижима и в последовательности срабатываний переход t1 срабатывает один раз, переходы t2 и t4 - по два раза, переход t3 не срабатывает.
Задача 4. Элементы математической логики и теории автоматовКонечный автомат задан графом, определенным в задаче 1. Вершины графа отождествляются с состояниями автомата таким образом, что множество состояний Q = {q1, q2 ,…, qn}. Переход автомата из одного состояния в другое осуществляется под воздействием множества входных сигналов X={x1, x2, x3, x4}. Переходы определяются законом отображения Г вершин графа, причем каждому переходу соответствует только одна из букв множества X. При задании графа эти буквы расставить произвольно.
Автомат позволяет вырабатывать выходные сигналы Y={y1, y2, y3}:
y1 - переход из состояния qi в состояние qi (петля);
y2- переход из состояния qiв qj при i<j;
y3- переход из состояния qi в qj при i>j.
Осуществить структурный синтез конечного автомата. Реализацию осуществить на элементах, указанных в табл.1, в соответствии с номером варианта. Обязательной является минимизация реализуемых функций.
Таблица 1
| № варианта | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Тип элементов | И НЕ | И ИЛИ НЕ | И НЕ | ИЛИ НЕ | И НЕ | И ИЛИ НЕ | И НЕ | ИЛИ НЕ | И ИЛИ НЕ | И НЕ |
| Тип триггера | D | JK | T | D | RS | RSD | D | JK | T | D |
Решение:
Множество вершин X = {x1, x2, x3, x4, x5, x6},
Вершины графа отожествляются с состояниями автомата таким образом, что множество состояний Q = {q1, q2, q3, q4, q5, q6}. Переход автомата из одного состояния в другое осуществляется под воздействием множества входных сигналов X={x1, x2, x3, x4}.
Автомат позволяет вырабатывать выходные сигналы Y={y1, y2, y3}.
На основании аналитического описания ориентированного графа из задания № 1 запишем закон отображения состояний автомата:
Гq1 = {q1 (x1/y1), q3 (x2/y2), q2 (x3/y2)},
Гq2 = {q4 (x3/y2), q1 (x4/y3), q3 (x1/y2)},
Гq3 = {q1 (x1/y3), q5 (x2/y2), q2 (x3/y3), q4 (x4/y2)},
Гq4 = {q2 (x1/y3), q6 (x2/y2), q3 (x3/y3), q5 (x4/y2)},
Гq5 = {q3 (x4/y3), q4 (x1/y3), q6 (x2/y2)}, Гq6= {q4 (x3/y3), q5 (x4/y3)}.
Обобщенная таблица переходов и выходов соответствующего конечного автомата представлена в табл.2.
Таблица 2
| X | Q | q1 | q2 | q3 | q4 | q5 | q6 |
| X1 | q1/y1 | q3/y2 | q1/y3 | q2/y3 | q4/y3 | ─ | |
| X2 | q3/y2 | ─ | q5/y2 | q6/y2 | q6/y2 | ─ | |
| X3 | q2/y2 | q4/y2 | q2/y3 | q3/y3 | ─ | q4/y3 | |
| X4 | ─ | q1/y3 | q4/y2 | q5/y2 | q3/y3 | q5/y3 | |
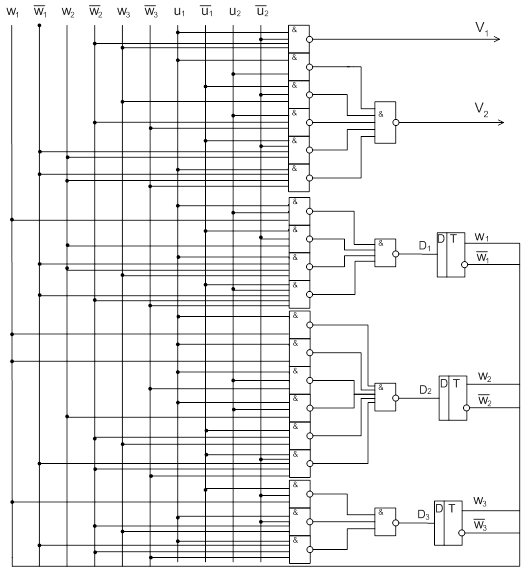
Осуществим структурный синтез автомата, заданного табл.1. В качестве элементов памяти используем D-триггеры, в качестве элементной базы используем логические элементы И-НЕ.
Количество букв входного алфавита n = 4
Количество входовp ≥ log2 n = log2 4 = 2;
Количество букв выходного алфавита m = 2
Количество выходовe ≥ log2 m = log2 3 = 2;
Количество состояний r = 6
Количество триггеровz ≥ log2 r = log2 6 = 3.
Приступаем к кодированию:
x | u | u1 | u2 |
|
| x1 | 1 | 0 | 5 | |
| x2 | 1 | 1 | 4 | |
| x3 | 0 | 0 | 5 | |
| x4 | 0 | 1 | 5 | |
| v1 | v2 |
| |
| y1 | 1 | 0 | 1 |
| y2 | 0 | 1 | 9 |
| y3 | 0 | 0 | 9 |
| q | w | w1 | w2 | w3 |
|
| q1 | 0 | 0 | 1 | 3 | |
| q2 | 0 | 1 | 0 | 3 | |
| q3 | 0 | 0 | 0 | 4 | |
| q4 | 1 | 0 | 0 | 4 | |
| q5 | 0 | 1 | 1 | 3 | |
| q6 | 1 | 1 | 0 | 2 | |
На основании результатов кодирования строим обобщенную таблицу переходов и выходов структурного автомата (табл.3), заменяя состояния, входные и выходные переменные их кодами.
Таблица 3
| u1u2 | w1w2w3 | 001 | 010 | 000 | 100 | 011 | 110 |
| 10 | 001/10 | 000/01 | 001/00 | 010/00 | 100/00 | ─ | |
| 11 | 000/01 | ─ | 011/01 | 110/01 | 110/01 | ─ | |
| 00 | 010/01 | 100/01 | 010/00 | 000/00 | ─ | 100/00 | |
| 01 | ─ | 001/00 | 100/01 | 011/01 | 000/00 | 011/00 | |
Используя таблицу переходов D-триггера и данные предыдущей таблицы, составим обобщенную таблицу функционирования структурного автомата (табл.4). Функции возбуждения трех триггеров обозначены через D1, D2, D3, соответственно.
Таблица 4
| u1 | u2 | w1 (t) | w2 (t) | w3 (t) | w1 (t+1) | w2 (t+1) | w3 (t+1) | v1 | v2 | D1 | D2 | D3 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | * | * | * | * | * | * | * | * |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | * | * | * | * | * | * | * | * |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | * | * | * | * | * | * | * | * |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | * | * | * | * | * | * | * | * |
| 1 | 1 | 1 | 1 | 0 | * | * | * | * | * | * | * | * |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
По этой таблице запишем СДНФ выходных функций V и функций возбуждения триггеров D1, D2, и D3, зависящих от набора переменных u1, u2, w1 (t), w2 (t), w3 (t). В результате получим систему логических функций для построения комбинационной части автомата:
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
Минимизируем функции согласно картам Карно:
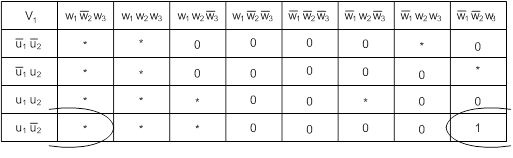
![]()
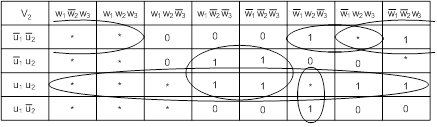
![]()

![]()
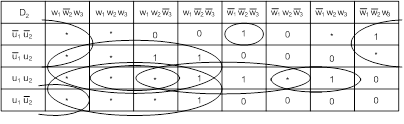
![]()
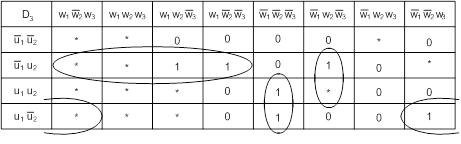
![]()
После минимизации имеем набор функций в базисе И-НЕ
![]()
![]() =
=
![]()
![]() .
.
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]() .
.
Функциональная схема структурного автомата:
Похожие работы
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... противоположные подходы, но нельзя считать ни один из них "юридически законным" или вытекающим из каких ни будь законов природы, нельзя считать стиль управления системой на основе системного анализа "правильным", "современным", "куль-турным". Другое дело — не знать о возможности применения системного подхода к вопросам управления — вот это неправильно, некультурно. Пример системного подхода ...
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... Рассела и во многом базируется на работе Бертрана Рассела и Альфреда Уайтхэда «Principia Mathematica» (этот фундаметальный трёхтомник математической логики до сих пор не издан на русском языке)[8]. Заключение Прародителем информатики является кибернетика, основанная американским математиком Норбертом Винером, опубликовавшим в 1948 году одноименную книгу. Основоположником ...
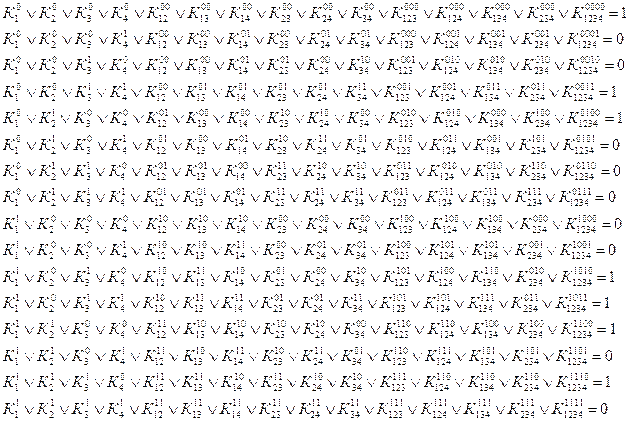
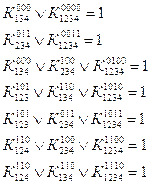
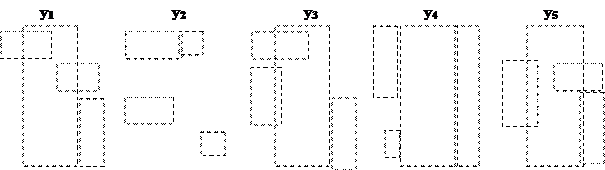
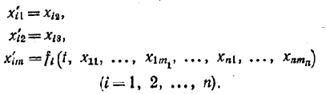

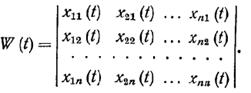
0 комментариев