ФОРМУЛЫ В MICROSOFT EXCEL

3 ФОРМУЛЫ В MICROSOFT EXCEL

Формулы представляют собой выражения, по которым выполняются вычисления на странице. Формула начинается со знака равенства (=).

Формула также может включать следующие элементы:

-   функции;

-   ссылки;

-   операторы (знак или символ, задающий тип вычисления в формуле. Существуют математические, логические операторы, операторы сравнения и ссылок);

-   константы (постоянное (не вычисляемое) значение).

Ссылка указывает на ячейку или диапазон ячеек листа и передает в Microsoft Excel сведения о расположении значений или данных, которые требуется использовать в формуле. При помощи ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать в нескольких формулах значение одной ячейки. Кроме того, можно задавать ссылки на ячейки других листов той же книги и на другие книги. Ссылки на ячейки других книг называются связями.

Существуют относительные, абсолютные и смешанные ссылки.

Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейку, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка.

Абсолютная ссылка ячейки в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется.

Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка столбцов приобретает вид $A1, $B1 и т. д. Абсолютная ссылка строки приобретает вид A$1, B$1 и т. д.

4 Общие сведения об алгоритмах.

Алгоритм – предписание последовательности действий, направленных на решение поставленной задачи. В Exel алгоритм записывается в виде последовательности операторов, включающих значение, ссылки и формулы.

Алгоритм обладает свойствами:

1)   однозначности – исключает произвольное толкование и приводит к одному и тому же результату при одинаковых исходных данных;

2)   массовости – применяется к другим подобным задачам;

3)   результативность – пошаговое выполнение задачи приводит к конечному результату.

Выделяется несколько типов алгоритмических структур:

1.   Линейная структура.

2.   Разветвляющая структура:

а)   с одной ветвью;

б)   с двумя ветвями;

в)   со множеством ветвей.

3.   Циклическая структура.

Принято выделять две циклические структуры с логическим условием до и после тела цикла.

Применительно к электронным таблицам это не совсем точно и справедливо, так как важен и способ организации выхода из цикла, а это:

-   бесконечный цикл;

-   вложенные циклические структуры;

-   цикл с заданным заранее количеством повторений;

-расчетно-динамический цикл (новый, характерный для электронной таблицы), количество повторений которого определяется в ходе пересчета таблицы, а параметры задаются в результате ссылки на ячейку, где содержаться расчетно-переменные данные.

-   итерационный цикл (количество повторений заранее неизвестно и зависит от осуществления или достижения заданной точности или последовательности приближений к искомому значению, где вычисление последующего члена производится через предыдущий член);

5 Метод половинного деления

 

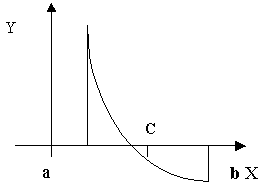
Этот метод отличается от выше рассмотренных методов тем, что для него не требуется выполнения условия, что первая и вторая производная сохраняют знак на интервале [a, b]. Метод половинного деления сходится для любых непрерывных функций f(x) в том числе недифференцируемых.

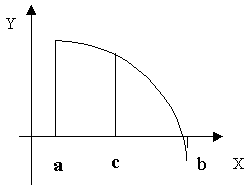
Разделим отрезок [a, b] пополам точкой Если (что практически наиболее вероятно), то возможны два случая: либо f(x) меняет знак на отрезке [a, c] (Рис. 1), либо на отрезке [c, b] (Рис. 2)

Рис. 1

Рис. 2

Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

6 РЕШЕНИЕ ЗАДАЧИ

Дана следующая функция:

F(х)=60*sin(5.5*x*pi/180)-69*cos(2.7*x*pi/180)-exp(x/192)-181/x

где Х изменяется от 0 до 400. Найти точки пересечения функции с точкой А (А=0).

Для нахождения точек пересечения используем метод половинного деления. Для этого от данной функции отнимем А (F(x)-А).

Построим алгоритм (приложение А).

Для того, что бы найти точки пересечения функции с точкой А, построим график (приложение В) по данным приведенным в таблице (приложение Г).

В графе Е2 введем формулу для нахождения значений где происходит смена знака =ЕСЛИ(В2*В3<=0; “смена знака”;” “).

По полученным данным найдем точки пересечения данной функции с точкой А в точках где происходит смена знака.

Например, смена знака происходит при значении Х=15, тогда в ячейку G2 введем значение Х1=15,а в ячейку G3 введем формулу =ЕСЛИ(J2*L2<=0;G2;I2). В ячейку Н2-значение Х2=20, а в ячейку Н3 введем формулу =ЕСЛИ(J2*L2<=0;I2;H2), это значит, что на этом интервале про исходит пересечение функции с координатной осью, то есть с точкой А. Для нахождения среднего значения в ячейку I2 введем формулу =(G2+H2)/2. В ячейки J2, K2, L2 введем формулы заданной в условии функции, где Х, для каждой из заданных ячеек, будет принимать значение Х1, Х2, Хср. соответственно.

Для того, чтобы определить на какой половине происходит смена знака в ячейку М2 введем формулу

 =ЕСЛИ(J2*L2<=0;”смена знака на 1-ой половине”;”cмена знака на 2-ой половине”).

В столбце N приведено количество шагов, за которое будит достигнута точность определения значения (х) не ниже 0,001.

Для определения погрешности, в ячейку О2 введем формулу =0-L2. Таким образом из приведенной таблицы видно, что значение Х с точностью до 0,001 определено за 14 шагов.

 

X1	X2	Xср	F(x1)	F(x2)	F(xcр)		Кол-во шагов	Погреш-ность
15,000	20,000	17,500	-6,129	5,665	1,368	смена знака на 1-ой половине	1	-1,3678
15,000	17,500	16,250	-6,129	1,368	-1,969	смена знака на 2-ой половине	2	1,9692
16,250	17,500	16,875	-1,969	1,368	-0,199	смена знака на 2-ой половине	3	0,1991
16,875	17,500	17,188	-0,199	1,368	0,610	смена знака на 1-ой половине	4	-0,6096
16,875	17,188	17,031	-0,199	0,610	0,212	смена знака на 1-ой половине	5	-0,2116
16,875	17,031	16,953	-0,199	0,212	0,008	смена знака на 1-ой половине	6	-0,0078
16,875	16,953	16,914	-0,199	0,008	-0,095	смена знака на 2-ой половине	7	0,0952
16,914	16,953	16,934	-0,095	0,008	-0,044	смена знака на 2-ой половине	8	0,0436
16,934	16,953	16,943	-0,044	0,008	-0,018	смена знака на 2-ой половине	9	0,0179
16,943	16,953	16,948	-0,018	0,008	-0,005	смена знака на 2-ой половине	10	0,0050
16,948	16,953	16,951	-0,005	0,008	0,001	смена знака на 1-ой половине	11	-0,0014
16,948	16,951	16,949	-0,005	0,001	-0,002	смена знака на 2-ой половине	12	0,0018
16,949	16,951	16,950	-0,002	0,001	0,000	смена знака на 2-ой половине	13	0,0002
16,950	16,951	16,950	0,000	0,001	0,001	смена знака на 1-ой половине	14	-0,0006

G H I J K L M N O

 По полученным данным с помощью мастера диаграмм построим график погрешности.

 

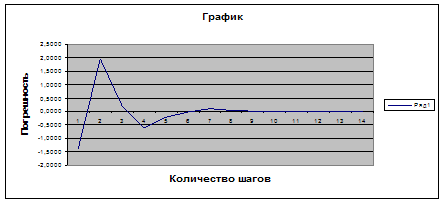
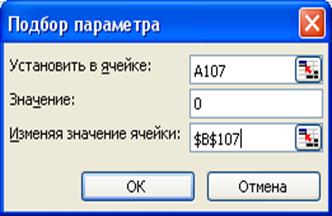
Для определения правильности решения произведем проверку с помощью подбора параметров.

Для этого в ячейку А107 введем формулу заданной функции, а в ячейку В107 введем значение Х при котором происходит смена знака. Далее необходимо поставить курсор в ячейку А107 и из меню сервис выбрать подбор параметра. В появившемся окне ввести необходимые данные, нажать кнопку ОК.

 

	А	В
105	Подбор параметров
106	F(X)	X
107	0,0000	16,950
108	0,0005	28,806
109	0,0003	54,235
110	0,0000	98,448
111	-0,0002	146,365
112	0,0000	158,039
113	0,0000	185,884
114	0,0001	230,163
115	0,0000	318,118
116	0,0009	361,607

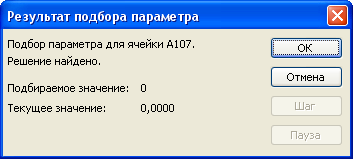
В появившемся окне Результат подбора параметра нужно нажать

кнопку ОК, после чего в ячейках А107 и В107 появится результат поиска.