Понятие оптимизационных задач и оптимизационных моделей

7 Понятие оптимизационных задач и оптимизационных моделей

 

Экономико-математические задачи, цель которых состоит в нахождении наилучшего, то есть оптимального с точки зрения одного или нескольких критериев варианта использования имеющихся ресурсов, называются оптимизационными.

Оптимизационные задачи решаются с помощью оптимизационных моделей методами математического программирования.

Математическое программирование – это раздел прикладной математики, который изучает задачи оптимизации и методы их решения с ориентацией на современные средства компьютерной техники.

Структура оптимизационной модели включает целевую функцию, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде также состоит из трех элементов:

·     управляемых переменных;

·     неуправляемых переменных;

·     формы функции (вида зависимости между ними).

Область допустимых решений – это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами и условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.

Главная задача математического программирования – это нахождение экстремума функций при выполнении указанных ограничений. Если система ограничений несовместима, то область допустимых решений является пустой.

Сущность задач оптимизации: определить значение переменных х₁, х₂,..., х_n, которые обеспечивают экстремум целевой функции Е, с учетом ограничений, наложенных на аргументы этой функции. При этом сложность решения задач зависит:

·     от вида функциональных зависимостей, то есть от связи функции Е с элементами решения;

·     от размерности задачи, то есть от количества элементов решения;

·     от вида и количества ограничений, накладываемых на элементы решения.

8 РЕШЕНИЕ ЗАДАЧИ

 

Кондитерская фабрика для производства трех видов карамели А, В и С использует три вида сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья на производство 1 кг. Карамели заданы в таблице.

Наименование сырья	Нормы расхода (кг./кг.)
	A	B	C
Сахарный песок	0,6	0,5	0,6
Патока	0,4	0,4	0,3
Фруктовое пюре	0,1	0,2	0,2

Запасы сырья на складе соответственно равны V1, V2 и V3 кг. Прибыль от реализации 1 кг. Продукции каждого вида определяется значениями РА, РВ и РС. Найти план производства карамели, обеспечивающий максимальную прибыль.

Запасы сырья (кг.)			Прибыль от реализации (руб./кг.)
V1	V2	V3	Pa	Pb	Pc
800	600	120	1,08	1,12	1,28

Подготовим задачу к решению.

Пусть х₁ – карамель вида А (кг.)

 х₂ – карамель вида В (кг.)

 х₃ – карамель вида С (кг.).

 Тогда система ограничений и целевая функция запишутся следующим образом:

Ра*Х1+Рв*Х2+Рс*Х3 =>mах (целевая функция);

х1*0,6+х2*0,5+х3*0,6<=800

х1*0,4+х2*0,4+х3*0,3<=600 ограничения на запасы сырья (сахарный

х1*0.1+х2*0,2+х3*0,2<=120 песок, патока, фруктовое пюре)

х1>=0; x2>=0; x3>=0;

x1, x2, x3- целые числа.

Для решения задачи в Excel запишем ее в виде, представленном на таблице 1.

Таблица 1 – Таблица для решения задачи

	Кг.		ограничение
х1	0		800	>=		0
х2	0		600	>=		0
х3	0		120	>=		0
Mах прибыль:		0

В соответствии с условием прибыль должна быть максимальной, поэтому в таблице 1 добавлена строка «Mах прибыль». В ней буду суммировать прибыль от реализации продукции.

Вызываю Поиск решения из меню Сервис.

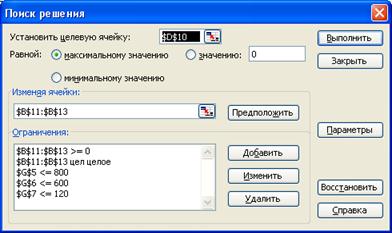
Определяю целевую ячейку – $D$8, устанавливаю переключатель в максимальное значение. Ввожу диапазон изменяемых ячеек ($B$11:$В$13) и вношу ограничения. Прежде всего, количество продукта не может быть отрицательным ($B$11:$В$13>=0), далее добавляю ограничения на запасы сырья, которое должно быть не более нормативного (800>=G$5; 600>=G$6; 120>=G$7). Нажимаю кнопку Выполнить.

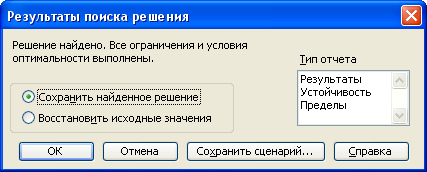
В появившемся окне Результаты поиска решения нажимаю кнопку ОК и получаю решение задачи (приложение Д).Из полученных данных видно, что максимальная прибыль при производстве карамели составила 1296 рублей, причем такая прибыль будет получена при производстве 1200кг. Карамели вида А.

Для проверки правильности решения введем дополнительные ограничения.

В первом варианте я ввела ограничение на карамель вида В и получила результат приведенный в таблице 1.

Таблица 1

Вариант 1				Запасы сырья (кг.)		Ограничение
Х1	1170			800	>=	709,5
Х2	15			600	>=	474
Х3	0			120	>=	120
Целевая функция	1280,4	Дополнительное ограничение		Х2>=15

Из таблицы видно, что прибыль по сравнению с данными полученными в приложении Д уменьшилась на 15,6 рублей, при этом уменьшилось и производство карамели вида А на 30кг.

Во втором варианте я ввела ограничение на карамель вида С и получила следующий результат

Вариант 2		Запасы сырья (кг.)		Ограничение
Х1	1180	800	>=	714
Х2	0	600	>=	475
Х3	10	120	>=	120
Целевая функция	1287,2	Дополнительное ограничение		Х3>=10

Из полученных данных видно, что прибыль, так же как и в первом варианте, уменьшилась относительно данных из приложения Д на 8,8 рубля, а производство карамели вида А уменьшилось на 20кг.

По полученным данным можно сделать вывод, что исходное решение задачи было верным.

ЗАКЛЮЧЕНИЕ

В данной курсовой работе были решены оптимизационные задачи с использованием программных средств Microsoft Excel.

В процессе решения первой задачи были построены: график функции F(x) с учетом параметра А=0 в заданном диапазоне значений переменной Х, которые изменяются в диапазоне от 0 до 400. Были найдены интервалы значений переменной Х в пределах, которых функция принимает значение параметра А. При использовании метода половинного деления были найдены значения переменной Х, при которых функция принимает значение параметра А, в соответствии с заданной точностью, равной 0,001. Проверка правильности вычислений была осуществлена с помощью «Подбора параметра».

Решение второй задачи осуществлялось с помощью «Поиска решений» средствами Microsoft Excel. Была составлена целевая функция и ограничения (соответствующие условию задачи). В результате был выбран оптимальный вариант решения задачи. Для проверки этого варианта были внесены дополнительные ограничения, которые показали, что исходно оптимальный вариант решения был верен.

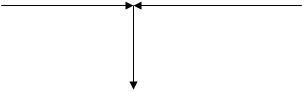
ПРИЛОЖЕНИЕ А

Начало

Описание F(х), А, ∆

Ввод а, b

с=(a+b)/2

F(a), F(b), F(c)

 нет да

(F(a)-A)+(F(c)-A)<=0

a: = c b: = c

нет да

(b-a)<=∆

Выво с,F(c), F(c)-A

Конец

ПРИЛОЖЕНИЕ Б

ПРИЛОЖЕНИЕ В

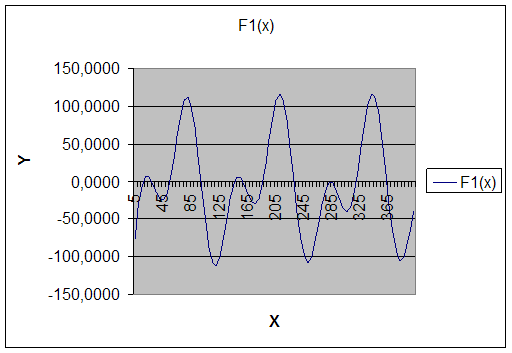
ПРИЛОЖЕНИЕ Г

А В С D E

X		F(x)		A		F(x)-A		Смена знака
5		-76,6150		0		-76,6150
10		-31,4838		0		-31,4838
15		-6,1292		0		-6,1292		смена знака
20		5,6646		0		5,6646
25		5,7512		0		5,7512		смена знака
30		-2,4673		0		-2,4673
35		-13,9441		0		-13,9441
40		-23,0017		0		-23,0017
45		-24,6667		0		-24,6667
50		-15,8988		0		-15,8988		смена знака
55		3,6061		0		3,6061
60		31,2394		0		31,2394
65		61,9826		0		61,9826
70		89,4820		0		89,4820
75		107,4577		0		107,4577
80		111,1312		0		111,1312
85		98,3486		0		98,3486
90		70,1426		0		70,1426
95		30,6047		0		30,6047		смена знака
100		-13,9123		0		-13,9123
105		-56,0851		0		-56,0851
110		-89,1227		0		-89,1227
115		-108,1489		0		-108,1489
120		-111,1603		0		-111,1603
125		-99,3512		0		-99,3512
130		-76,7403		0		-76,7403
135		-49,1871		0		-49,1871
140		-23,0264		0		-23,0264
145		-3,6307		0		-3,6307		смена знака
150		5,7743		0		5,7743
155		4,7747		0		4,7747		смена знака
160		-4,2332		0		-4,2332
165		-16,7039		0		-16,7039
170		-27,1093		0		-27,1093
175		-30,3377		0		-30,3377
180		-23,0020		0		-23,0020
185		-4,3520		0		-4,3520		смена знака
190		23,4221		0		23,4221
195		55,5727		0		55,5727
200		85,7823		0		85,7823
205		107,5385		0		107,5385
210		115,5876		0		115,5876
215		107,1397		0		107,1397
220		82,5521		0		82,5521
225		45,3337		0		45,3337
230		1,4645		0		1,4645		смена знака
	235		-41,8225		0		-41,8225
	240		-77,5282		0		-77,5282
	245		-100,3165		0		-100,3165
	250		-107,5698		0		-107,5698
	255		-99,8416		0		-99,8416
	260		-80,6115		0		-80,6115
	265		-55,4037		0		-55,4037
	270		-30,4751		0		-30,4751
	275		-11,3711		0		-11,3711
	280		-1,6789		0		-1,6789
	285		-2,2580		0		-2,2580
	290		-11,1210		0		-11,1210
	295		-23,9866		0		-23,9866
	300		-35,3741		0		-35,3741
	305		-39,9858		0		-39,9858
	310		-34,0560		0		-34,0560
	315		-16,3539		0		-16,3539		смена знака
	320		11,3948		0		11,3948
	325		44,7702		0		44,7702
	330		77,5536		0		77,5536
	335		103,0577		0		103,0577
	340		115,5964		0		115,5964
	345		111,7635		0		111,7635
	350		91,2325		0		91,2325
	355		56,8943		0		56,8943
	360		14,2986		0		14,2986		смена знака
	365		-29,4800		0		-29,4800
	370		-67,3017		0		-67,3017
	375		-93,4252		0		-93,4252
	380		-104,6518		0		-104,6518
	385		-100,9012		0		-100,9012
	390		-85,0963		0		-85,0963
	395		-62,3901		0		-62,3901
	400		-38,9164		0		-38,9164		смена знака

ПРИЛОЖЕНИЕ Д

A	B	C	D	E	F	G
Наименование сырья	Нормы расхода (кг./кг.)			Запасы сырья (кг.)		Ограничение
	A	B	C
Сахарный песок	0,6	0,5	0,6	800	>=	720
Патока	0,4	0,4	0,3	600	>=	480
Фруктовое пюре	0,1	0,2	0,2	120	>=	120
Прибыль от реализации (руб./кг.)	1,08	1,12	1,28
		Целевая функция	1296
x1	1200			А=х1
x2	0			В=х2
x3	0			С=х3

Литература

1.         Банди Б. Основы линейного программирования. – М.: Радио и связь, 1989.

2.          Карпов Б. Microsoft Excel 2000. Справочник.- Питер, 2002.

3.          Семенищенков А. Microsoft Excel. Параметры и методы практического программирования. – Брянск, 1998.

4.          Рычков В. Microsoft Excel 2000. – Питер, 2000.