Навигация
Полученные оценки модели и ее параметров позволяют использовать ее для прогноза
2. Полученные оценки модели и ее параметров позволяют использовать ее для прогноза.
Рассчитаем ![]() . Тогда
. Тогда ![]() .
.
3. Средняя ошибка прогноза
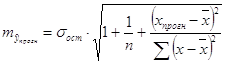 ,
,
где
 ,
,
![]() .
.
Строим доверительный интервал с заданной доверительной вероятностью ![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Найденный интервальный прогноз достаточно надежен (доверительная вероятность ![]() ) и достаточно точен, т.к.
) и достаточно точен, т.к. ![]() .
.
Задание 2
Имеются данные о деятельности крупнейших компаний в течение двенадцати месяцев 199Х года. Данные приведены в табл. 4.
Известны – чистый доход (у), оборот капитала (х1), использованный капитал (х2) в млрд у.е.
Таблица 4| у | х1 | х2 |
| 1,5 | 5,9 | 5,9 |
| 5,5 | 53,1 | 27,1 |
| 2,4 | 18,8 | 11,2 |
| 3,0 | 35,3 | 16,4 |
| 4,2 | 71,9 | 32,5 |
| 2,7 | 93,6 | 25,4 |
| 1,6 | 10,0 | 6,4 |
| 2,4 | 31,5 | 12,5 |
| 3,3 | 36,7 | 14,3 |
| 1,8 | 13,8 | 6,5 |
| 2,4 | 64,8 | 22,7 |
| 1,6 | 30,4 | 15,8 |
Задание:
1. Рассчитайте параметры линейного уравнения множественной регрессии.
2. Дайте оценку силы связи факторов с результатом с помощью средних коэффициентов эластичности.
3. Оцените статистическую зависимость параметров и уравнения регрессии в целом с помощью соответственно критериев Стьюдента и Фишера (α=0,01).
4. Рассчитайте среднюю ошибку аппроксимации. Сделайте вывод.
5. Составьте матрицы парных и частных коэффициентов корреляции и укажите информативные факторы.
6. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение
Результаты расчетов приведены в табл. 5.
Таблица 5
| y | x1 | x2 | yx1 | yx2 | x1x2 | x12 | x22 | y2 | |
| 1,5 | 5,9 | 5,9 | 8,85 | 8,85 | 34,81 | 34,81 | 34,81 | 2,25 | |
| 5,5 | 53,1 | 27,1 | 292,05 | 149,05 | 1439,01 | 2819,61 | 734,41 | 30,25 | |
| 2,4 | 18,8 | 11,2 | 45,12 | 26,88 | 210,56 | 353,44 | 125,44 | 5,76 | |
| 3 | 35,3 | 16,4 | 105,90 | 49,20 | 578,92 | 1246,09 | 268,96 | 9 | |
| 4,2 | 71,9 | 32,5 | 301,98 | 136,50 | 2336,75 | 5169,61 | 1056,25 | 17,64 | |
| 2,7 | 93,6 | 25,4 | 252,72 | 68,58 | 2377,44 | 8760,96 | 645,16 | 7,29 | |
| 1,6 | 10 | 6,4 | 16,00 | 10,24 | 64,00 | 100,00 | 40,96 | 2,56 | |
| 2,4 | 31,5 | 12,5 | 75,60 | 30,00 | 393,75 | 992,25 | 156,25 | 5,76 | |
| 3,3 | 36,7 | 14,3 | 121,11 | 47,19 | 524,81 | 1346,89 | 204,49 | 10,89 | |
| 1,8 | 13,8 | 6,5 | 24,84 | 11,70 | 89,70 | 190,44 | 42,25 | 3,24 | |
| 2,4 | 64,8 | 22,7 | 155,52 | 54,48 | 1470,96 | 4199,04 | 515,29 | 5,76 | |
| 1,6 | 30,4 | 15,8 | 48,64 | 25,28 | 480,32 | 924,16 | 249,64 | 2,56 | |
|
| 32,4 | 465,8 | 196,7 | 1448,33 | 617,95 | 10001,03 | 26137,30 | 4073,91 | 102,96 |
| Средн. | 2,7 | 38,8 | 16,4 | 120,69 | 51,50 | 833,42 | - | - | 65,80 |
|
| 1,2 | 27,1 | 8,8 | - | - | - | - | - | - |
|
| 1,4 | 732,4 | 77,2 | - | - | - | - | - | - |
Рассматриваем уравнение вида:
![]() .
.
Параметры уравнения можно найти из решения системы уравнений:
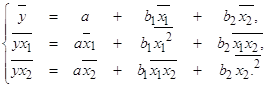
Или, перейдя к уравнению в стандартизированном масштабе:
![]() , где
, где
 – стандартизированные переменные,
– стандартизированные переменные,
![]() – стандартизированные коэффициенты:
– стандартизированные коэффициенты:
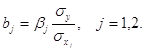
Коэффициенты ![]() определяются из системы уравнений:
определяются из системы уравнений:

![]()
 ,
,  ;
;
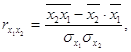
 ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() .
.
Стандартизированная форма уравнения регрессии имеет вид:
![]() .
.
Естественная форма уравнения регрессии имеет вид:
![]() .
.
Для выяснения относительной силы влияния факторов на результативный признак рассчитываются средние коэффициенты эластичности:
 ,
,
![]() ,
,
![]() .
.
Следовательно, при увеличении оборота капитала (x1) на 1% чистый доход (y) уменьшается на 0,14% от своего среднего уровня. При повышении использованного капитала на 1% чистый доход повышается на 0,73% от своего среднего уровня.
Линейные коэффициенты частной корреляции для уравнения определяются следующим образом:
 ,
,
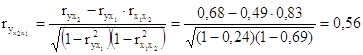 .
.
Линейный коэффициент множественной корреляции рассчитывается по формуле
![]() .
.
Коэффициент множественной детерминации ![]() .
.
 ,
,
где
![]() - объем выборки,
- объем выборки,
![]() - число факторов модели.
- число факторов модели.
В нашем случае
![]() .
.
Так как ![]() , то
, то ![]() и потому уравнение незначимо.
и потому уравнение незначимо.
Выясним статистическую значимость каждого фактора в уравнении множественной регрессии.
Для этого рассчитаем частные ![]() -статистики.
-статистики.
 .
.
Так как ![]() , то
, то ![]() и следует вывод о нецелесообразности включения в модель фактора
и следует вывод о нецелесообразности включения в модель фактора ![]() после фактора
после фактора ![]() .
.
 .
.
Так как ![]() , то следует вывод о нецелесообразности включения в модель фактора
, то следует вывод о нецелесообразности включения в модель фактора ![]() после фактора
после фактора ![]() .
.
Результаты расчетов позволяют сделать вывод :
1) о незначимости фактора ![]() и нецелесообразности включения его в уравнение регрессии;
и нецелесообразности включения его в уравнение регрессии;
2) о незначимости фактора ![]() и нецелесообразности включения его в уравнение регрессии.
и нецелесообразности включения его в уравнение регрессии.
Задание 3
1. Используя необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое уравнение модели.
2. Определите тип модели.
3. Определите метод оценки параметров модели.
4. Опишите последовательность действий при использовании указанного метода.
5. Результаты оформите в виде пояснительной записки.
Модель денежного и товарного рынков:
Rt = a1+b12Yt+b14Mt+e1,
Yt = a2+b21Rt+ b23It+ b25Gt+e2,
It = a3+b31Rt+e3,
где
R – процентные ставки;
Y – реальный ВВП;
M – денежная масса;
I – внутренние инвестиции;
G – реальные государственные расходы.
Решение
1. Модель имеет три эндогенные (RtYtIt) и две экзогенные переменные (MtGt).
Проверим необходимое условие идентификации:
1-е уравнение: D=1, H=2, D+1=H - уравнение идентифицировано.
2-е уравнение: D=1, H=1, D+1=2 - уравнение сверхидентифицировано.
3-е уравнение: D=1, H=2, D+1=H - уравнение идентифицировано.
Следовательно, необходимое условие идентифицируемости выполнено.
Проверим достаточное условие:
В первом уравнении нет переменных It, Gt
Строим матрицу:
| It | Gt | |
| 2 ур. | b23 | b23 |
| 3 ур. | 0 | 0 |
det M = det ![]() , rank M =2.
, rank M =2.
Во втором уравнении нет переменных Mt
det M ¹ 0
В третьем уравнении нет переменных Yt, Mt, Gt
Строим матрицу:
det M ![]() /
/
Следовательно, достаточное условие идентифицируемости выполнено.
Система точно идентифицируема.
Похожие работы
... уравнения. 4. Найти среднюю ошибку аппроксимации. 5. Рассчитать прогнозное значение результата, если прогнозное значение факторов составит: х1 = 35 лет, х2 = 10 лет, х3 = 20 штук в смену. Решение. Для оценки мультиколлинеарности факторов используем определитель матрицы парных коэффициентов корреляции между факторами. Определим парные коэффициенты корреляции. Для этого рассчитаем ...
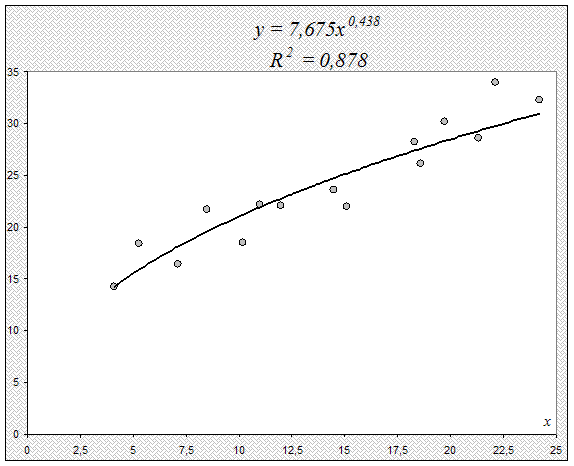
... а также любые колебания, в которых прослеживается закономерность. В качестве примера можно назвать модель экспоненциального сглаживания Брауна. 3. Пример проведения прогнозирования прибыли с использованием пакета SPSS Постановка задачи: Необходимо построить модель, дающую возможность предсказывать размер прибыли некоторой торговой фирмы, если известны данные о ежемесячной прибыли за последние ...
... , и , то можно предположить о правильном распределении объектов и уже существующих двух классах и верно выполненной классификации объектов подмножества М0. 3.2 Пример решения задачи дискриминантным анализом в системе STATISTICA Исходя из данных по 10 странам (рис. 3.1), которые были выбраны и отнесены к соответствующим группам экспертным методом (по уровню медицинского обслуживания), ...
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...



0 комментариев