Навигация
Оцінка значущості параметрів моделі. Побудування інтервалів довіри
3. Оцінка значущості параметрів моделі. Побудування інтервалів довіри.
I. Оцінімо параметр b0. Для цього розрахуємо коефіцієнт статистику t0.
b0 = 1,3053
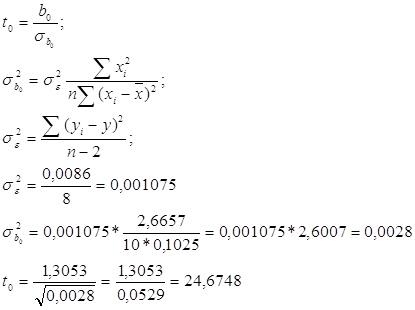
Висуваємо гіпотези:
H0: β0 = 0
H1: β0 ≠ 0
Рівень значущості α = 0,05
Кількість ступенів свободи k = n – 2; k = 10 – 2 = 8.
За допомогою таблиці теста Стьюдента визначимо, що t0,05 = 2,31.
![]()
Висновок: за п’ятивідсоткового рівня значущості можна стверджувати, що з імовірністю, більшою за95% оцінка b0 є статистично значущою, що потребує розрахунку інтервалу довіри.
β0 = b0 ± t0,05*σb0 = 1,3053 ± 2,31*0,0529 = 1,3053 ± 0,122199
Р(1,183101< β0 < 1,427499) = (1 – α) *100% = 95%
Таким чином, в генеральній сукупності β0 з імовірністю 95% знаходиться в інтервалі (1,183101; 1,427499).
II. Оцінімо параметр b1.
b1 = 0,0115
Визначимо t-статистику для b1:
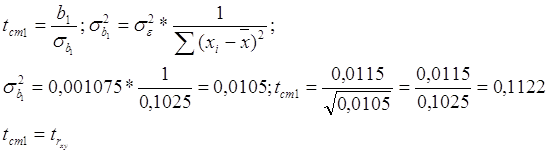
В нашому випадку tст1 ≈ trxy. Приблизна рівність допустима (trxy = 0,1166) і означає, що в розрахунках були погрішності, якими можна зневажати.
Висуваємо гіпотези:
H0: β0 = 0
H1: β0 ≠ 0
tст1 = 0,1122
Рівень значущості α = 0,05.
Кількість ступенів свободи k = n – 2; k = 10 – 2 = 8.
За допомогою таблиці теста Стьюдента визначимо, що t0,05 = 2,31.
tст1< t0,05.
Висновок: за п’ятивідсоткового рівня значущості можна стверджувати, що з імовірністю, більшою за 95%, оцінка параметра b1 не є статистично значущою, звідки робимо висновок, що інтервал довіри не розраховується.
4. Точкове прогнозування yn+1 для ![]() , де р = 0,95.
, де р = 0,95.
ŷn+1 = b0 + b1*xn+1
ŷn+1 = 1,3053 + 0,0115*11 = 1,4318.
Висновок: отже, за прогнозними даними в 11-му періоді значення залежної змінної дорівнюватиме 1,4318. Але, як було вказано раніше, ці прогнозні значення навряд чи можна вважати достовірними, тому що коефіцієнти детермінації та кореляції відповідають дуже слабкому рівню зв’язку між змінними.
Розв’язання завдання 2
1. Кореляційна матриця.
За допомогою Пакету аналізу Excel побудуємо кореляційну матрицю, використовуючи операцію Кореляція (рис.1).
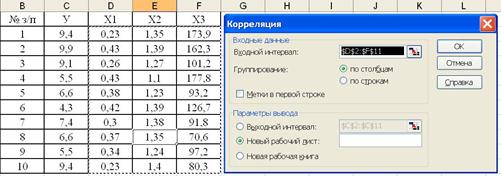
Рис.1. Процес побудови кореляційної матриці.
Таблиця 1. Кореляційна матриця Excel
| Стовпчик 1 | Стовпчик 2 | Стовпчик 3 | |
| Стовпчик 1 | 1 | ||
| Стовпчик 2 | -0,30202801 | 1 | |
| Стовпчик 3 | 0,279578475 | -0,25820294 | 1 |
За допомогою команди Регресія Аналізу даних Excel (рис.2) проведемо регресійний аналіз.

Рис.2. Процес проведення регресійного аналізу.
Виходячи з даних таблиці 2, маємо наступні висновки:
1. Коефіцієнт множинної детермінації показує, що приблизно 50% зміни змінної У залежить від змін змінних Х. Це свідчить про доволі щільний зв’язок, враховуючи як мінімум три фактори впливу (три змінні).
2. Рівень спостережень (10) дозволяє судити про достатній рівень для оцінки множинної регресії.
3. F більша за значимість F. Це означає, що з 5% -м ризиком помилки можна стверджувати, що з імовірністю, більшою за 95%, можна стверджувати, що між змінними Х1, Х2 та Х3 існує лінійна залежність.
4. Мультиколлінеарність – це становище, за якого одна чи більше незалежних змінних, що входять до рівняння регресії, є точними лінійними функціями від однієї чи більше інших незалежних змінних того самого рівняння. Наявність мультиколлінеарності визначає коефіцієнт детермінації. Його значення, що свідчить про залежність незалежних змінних одна від одної. Отже, спостерігаємо наявність мультиколлінеарності.
Виходячи з результатів даного аналізу маємо наступне рівняння регресії (найкраще):
![]()
Таблиця 2
Результати регресійного аналізу Excel
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0,711739446 | |||||||
| R-квадрат | 0,506573039 | |||||||
| Нормированный R-квадрат | 0,259859559 | |||||||
| Стандартная ошибка | 1,70239339 | |||||||
| Наблюдения | 10 | |||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 3 | 17,85214 | 5,950713 | 2,053285 | 0, 208003285 | |||
| Остаток | 6 | 17,38886 | 2,898143 | |||||
| Итого | 9 | 35,241 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 1,705455824 | 9,48843 | 0,179741 | 0,863273 | -21,51189547 | 24,92280712 | -21,51189547 | 24,92280712 |
| Переменная X 1 | -14,451294 | 7,646333 | -1,88996 | 0,107657 | -33,16119756 | 4,258609463 | -33,16119756 | 4,258609463 |
| Переменная X 2 | 6,506205971 | 6, 202293 | 1,049 | 0,334583 | -8,670259371 | 21,68267131 | -8,670259371 | 21,68267131 |
| Переменная X 3 | 0,017365132 | 0,015039 | 1,154705 | 0,292119 | -0,019432971 | 0,054163235 | -0,019432971 | 0,054163235 |
Додаток 1
Таблиця проміжних розрахунків до Завдання 1.
| i | x | y | х2 | х*y | ŷ | у-уср | (у-уср) 2 | (ŷ - уср) 2 | (у - ŷ) 2 | х-х | (х-х) 2 | (х-х) (у-у) |
| 1 | 0,15 | 1,35 | 0,0225 | 0, 2025 | 1,3071 | 0,0400 | 0,0016 | 0,00000861 | 0,0018 | -0,2550 | 0,0650 | -0,0102 |
| 2 | 0,34 | 1,39 | 0,1156 | 0,4726 | 1,3093 | 0,0800 | 0,0064 | 0,00000056 | 0,0065 | -0,0650 | 0,0042 | -0,0052 |
| 3 | 0,09 | 1,27 | 0,0081 | 0,1143 | 1,3064 | -0,0400 | 0,0016 | 0,00001314 | 0,0013 | -0,3150 | 0,0992 | 0,0126 |
| 4 | 0,05 | 1,1 | 0,0025 | 0,055 | 1,3059 | -0,2100 | 0,0441 | 0,00001669 | 0,0424 | -0,3550 | 0,1260 | 0,0746 |
| 5 | 0,48 | 1,23 | 0,2304 | 0,5904 | 1,3109 | -0,0800 | 0,0064 | 0,00000074 | 0,0065 | 0,0750 | 0,0056 | -0,0060 |
| 6 | 0,41 | 1,39 | 0,1681 | 0,5699 | 1,3101 | 0,0800 | 0,0064 | 0,00000000 | 0,0064 | 0,0050 | 0,0000 | 0,0004 |
| 7 | 0,62 | 1,38 | 0,3844 | 0,8556 | 1,3125 | 0,0700 | 0,0049 | 0,00000612 | 0,0046 | 0,2150 | 0,0462 | 0,0151 |
| 8 | 0,5 | 1,35 | 0,25 | 0,675 | 1,3111 | 0,0400 | 0,0016 | 0,00000120 | 0,0015 | 0,0950 | 0,0090 | 0,0038 |
| 9 | 1,2 | 1,24 | 1,44 | 1,488 | 1,3191 | -0,0700 | 0,0049 | 0,00008369 | 0,0063 | 0,7950 | 0,6320 | -0,0557 |
| 10 | 0,21 | 1,4 | 0,0441 | 0,294 | 1,3078 | 0,0900 | 0,0081 | 0,00000504 | 0,0085 | -0, 1950 | 0,0380 | -0,0176 |
| Σ | 4,05 | 13,1 | 2,6657 | 5,3173 | 0,0860 | 0,00013578 | 0,0859 | 1,0255 | 0,0118 | |||
| Σ/і | 0,4050 | 1,3100 | 0,2666 | 0,5317 | 0,0086 | 0,00001358 | 0,0086 | 0,1025 | 0,0012 |
Похожие работы
... і мультиколінеарності не існує. Відповідь: Коефіцієнт детермінації R2=0.863,автокореляція та загальна мультиколінеарність відсутні. Завдання 4. Проаналізуйте модель виробничої функції типу Кобба-Дугласа,що описує залежність між продуктивністю праці y=y/l та фондоозброєністю x=k/l з урахуванням впливу технічного ...
... комбiнацiю просторової i часової вибірок n × m × T. Проблема формування сукупності спостережень та її однорiдностi досить важлива в економетричному моделюванні, бо економетрична модель кiлькiсно описує закономiрнiсть формування економічних процесів та явищ. А ця закономiрнiсть доволі повно може проявитись лише тоді, коли сукупність спостережень достатньо велика. Якщо дослідник задає ...
... інтервалу [1,36; 2,64], то можна говорити про відсутність автокореляції. Подальше проведення розрахунків за критерієм фон-Неймана та застосування методу Ейткена є недоцільним. ЗАДАЧА 4 ОЦІНКА ПАРАМЕТРІВ СИСТЕМИ ЕКОНОМЕТРИЧНИХ РІВНЯНЬ Оцінити параметри економетричної моделі, що складається з двох рівнянь: (4.1) Перше рівняння відображає залежність грошового обігу від оборотності грошей ...
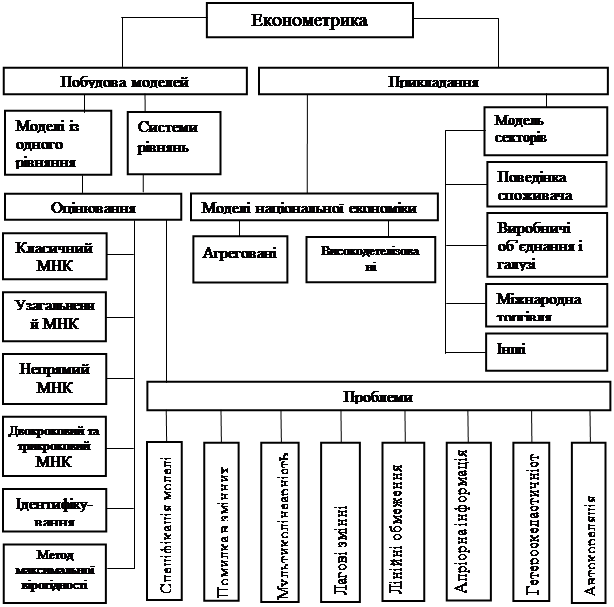
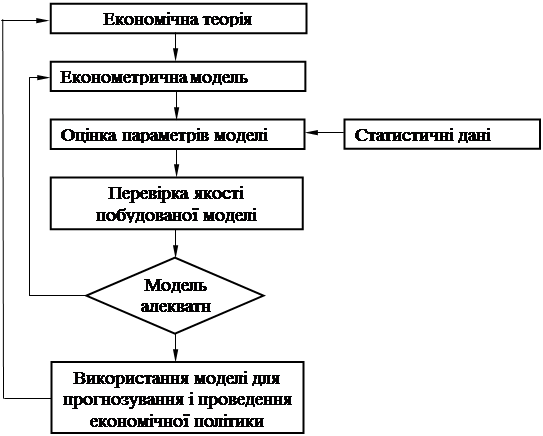
... ); - оцінка параметрів побудованої моделі; - перевірка якості знайдених параметрів моделі; - використання побудованих моделей, для пояснення поводження досліджуваних економічних показників, прогнозування й пророкування. Структура економетрики В економетриці, як дисципліні на стику економіки (включаючи менеджмент) і статистичного аналізу, природно виділити ...
0 комментариев