Навигация
1.3 Игры с природой
Модели в виде стратегических игр, в экономической практике могут не в полной мере оказаться адекватными действительности, поскольку реализация модели предполагает многократность повторения действий (решений), предпринимаемых в похожих условиях. В реальности количество принимаемых экономических решений в неизменных условиях жестко ограничено. Нередко экономическая ситуация является уникальной, и решение в условиях неопределенности должно приниматься однократно. Это порождает необходимость развития методов моделирования принятия решений в условиях неопределенности и риска.
Традиционно следующим этапом такого развития являются так называемые игры с природой. Формально изучение “игр с природой“, так же как и стратегических, должно начинаться с построения платежной матрицы, что является, по существу, наиболее трудоемким этапом подготовки принятия решения. Ошибки в платежной матрице не могут быть компенсированы никакими вычислительными методами и приведут к неверному итоговому результату.
Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игроком 1. Игрок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре. Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально, хотя вполне могут встретиться ситуации, в которых «игроком» 2 действительно может быть природа (например, обстоятельства, связанные с погодными условиями или с природными стихийными силами).
2. ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ СМЕШАННЫХ СТРАТЕГИЙ
2.1 Постановка задачи
Выбрать оптимальный режим работы новой системы ЭВМ, состоящей из двух ЭВМ типов А1 и А2. Известны выигрыши от внедрения каждого типа ЭВМ в зависимости от внешних условий, если сравнить со старой системой.
При использовании ЭВМ типов А1 и А2 в зависимости от характера решаемых задач В1 и В2 (долговременные и краткосрочные) будет разный эффект. Предполагается, что максимальный выигрыш соответствует наибольшему значению критерия эффекта от замены вычислительной техники старого поколения на ЭВМ A1 и А2.
Итак, дана матрица игры (табл. 1), где A1, А2 - стратегии руководителя; В1, В2 - стратегии, отражающие характер решаемых на ЭВМ задач.
Таблица 2.1.
| Игрок 2 Игрок 1 | В1 | В2 | ai |
| А1 | 0,3 | 0,8 | 0,3 |
| А2 | 0,7 | 0,4 | 0,4 |
| bj | 0,7 | 0,8 |
Требуется найти оптимальную смешанную стратегию руководителя и гарантированный средний результат g, т.е. определить, какую долю времени должны использоваться ЭВМ типов A1 и А2.
2.2 Описание алгоритма решения
Запишем условия в принятых обозначениях:
а11 = 0,3; а12 = 0,8; а21 = 0,7; а22 = 0,4.
Определим нижнюю и верхнюю цены игры:
a1 = 0,3; a2 = 0,4; a = 0,4; b1=0,7; b2 = 0,8; b = 0,7.
Получаем игру без седловой точки, так как
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
Максиминная стратегия руководителя вычислительного центра – А2.
Для этой стратегии гарантированный выигрыш равен a = 0,4 (40%) по сравнению со старой системой.
Определим g, pl и р2 графическим способом (рис. 2.1).
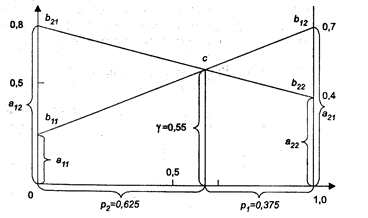
Рис. 2.1. Графическая интерпретация алгоритма решения
Алгоритм решения:
1. По оси абсцисс отложим отрезок единичной длины.
2. По оси ординат отложим выигрыши при стратегии А1.
3. На вертикали в точке 1 отложим выигрыши при стратегии А2.
4. Проводим прямую b11b12, соединяющую точки а11, а21.
5. Проводим прямую b21b22, соединяющую точки а12, а22.
6. Определяем ординату точки пересечения с линий b11b12 и b21b22. Она равна g.
7. Определим абсциссу точки пересечения с. Она равна р2, а р1 = l – р2.
Выпишем решение и представим оптимальную стратегию игры:
р1 = 0,375; (2.3)
р2 = 0,625; ![]() (2.4)
(2.4)
g =0,55. (2.5)
Вывод. При установке новой системы ЭВМ, если неизвестны условия решения задач заказчика, на работу ЭВМ А1 должно приходиться 37,5% времени, а на работу ЭВМ А2 - 62,5%. При этом выигрыш составит 55% по сравнению с предыдущей системой ЭВМ.
Похожие работы
... на конкретные факты. Таким образом, интерес к процессу, способу решения превращается в интерес к теории, к основанию знания. Глава 2. Эмпирическое исследование влияния сюжетно-ролевой игры на мотивацию дошкольников 2.1 Цели, задачи, методы, база исследования и организация практической работы по изучению мотивации старших дошкольников Мотивационная готовность предполагает наличие у ...
... теорий мотивации имело явно эволюционный, а не революционный характер. Они эффективно используются в решении ежедневно возникающих задач побуждения людей к эффективному труду. 1.3.1. Теории содержания мотивации Содержательные теории мотивации в первую очередь стараются определить потребности и факторы, побуждающие людей к действию, особенно при определении объема и содержания работы. При ...
... которыми оно пользуется в своем воздействии на людей, - это видимость и обман»33. Как видим, именно через такое воззрение на искусство мы можем определить отношение одного из представителей немецкой классической философии к категории игры. Итак, Гегель определяет искусство как «приятную игру». В этом прямая перекличка с Кантом - отнесение игры к сфере незаинтересованного удовольствия. Теперь ...
... различные качества и особый общественно-культурный смысл. Многие исследователи игры связывают ее происхождение с религиозной культурой, к примеру, народные и праздничные игры, сохранившиеся в духовной жизни людей, возникшие из языческих религиозных обрядов. П.Лавров, — русский философ, социолог, публицист (1823-1900), в работе "Переживания доисторического периода" указывает на прямую связь забав с ...

0 комментариев