Определение расчетных сочетаний усилий в сечениях рамы

6. Определение расчетных сочетаний усилий в сечениях рамы

Нагрузки от собственного веса конструкций, снега и ветра действуют на раму в сочетании друг с другом. Расчет рамы следует выполнить с учетом наиболее неблагоприятных сочетаний нагрузок или соответствующих им усилий, установленных в соответствии с требованиями пп. 1.10 – 1.13 СНиП Нагрузки и воздействия.

 Для проектируемой рамы составляем основные сочетания усилий (п.1.11 СНиП Нагрузки и воздействия). Первое сочетание состоит из усилий от постоянной и одной кратковременной (снеговой) нагрузок, второе - из усилий от постоянной и двух кратковременных (снег + ветер) нагрузок, умноженных на коэффициент сочетаний y₂ = 0,9 (п. 1.12 СНиП Нагрузки и воздействия). Ввиду малости изгибающих моментов в раме от ветровой нагрузки можно ограничиться составлением только первого основного сочетания усилий.

Расчетные изгибающие моменты в сечениях рамы, вычисленные при одновременном действии на раму постоянной нагрузки и снеговой в трех вариантах, приведены в таблице 3.

Значения расчетных продольных усилий N, соответствующих расчетным значениям изгибающих моментов М_w, определяются в разделе “Конструктивный расчет”.

7. Конструктивный расчет рамы

 

7.1. Расчет рамы на прочность

Рама работает на сжатие и поперечный изгиб. Расчет на прочность трехшарнирных рам в их плоскости допускается выполнять по правилам расчета сжато-изгибаемых элементов с расчетной длиной, равной длине полурамы по осевой линии СНиП “Нормы проектирования. Деревянные конструкции”, п. 6.28.

 На участке рамы с размерами поперечного сечения b x h₁= 135 х 752мм наибольший расчетный изгибающий момент относительно оси w - w действует в сечении № 2 (карнизный узел), М_w2 = 113,33 кНм (см. табл. 3). Момент растягивает наружную кромку сечения. Значение расчетной продольной силы, действующей по расчетной оси рамы в сечении № 2 при таком же сочетании нагрузок, как и для момента M_w2, найдем по формуле:

N₂ = [R_A - (q • g_n + p • g_n) x₂] • Sin φ₂ + H_A•Cos φ₂ ,здесь

R_A = (q • g_n + p •g_n) • l /2 = (1,941•0,95 + 7,2•0,95) • 15/2 = 65 кН

H_A = (q • g_n + p • g_n) • l ²/(8 • f) =(1,941•0,95 + 7,2•0,95)•15 ²/(8 • 5,075)=48 кН

φ₂ = arcSin [(r_p – x₂) / r_p] = arcSin [(3035 – 637) / 3035] = 52°

Тогда

N₂ = [65 - (1,941 • 0,95 + 7,2 • 0,95) • 0,637] • Sin 52 + 48•Cos 52 = 76,4 кН

На участке рамы с размерами поперечного сечения b x h₂ = 135 x 384мм наибольший расчетный изгибающий момент относительно оси w – w действует в сечении № 5, М_w5 = 26,18 кНм (см. табл. 3). Момент растягивает наружную кромку сечения. Значение расчетной продольной силы, действующей по расчетной оси рамы в сечении № 5 при таком же сочетании нагрузок, как и для момента М_w5, найдем по результатам расчета по формуле:

N₅ = (R_A – q • g_n • x₅) • Sin α + H_A • Cos α, здесь

R_A = q • g_n • l /2 + p • g_n • l /8 = 1,941 • 0,95 • 15/2 + 7,2 • 0,95 • 15/8=26,64кН

H_A = q • g_n • l ²/(8•f) + p • g_n • l ²/(16•f) =

= 1,941 • 0,95 • 15 ²/(8•5,075) + 7,2 • 0,95 • 15²/(16•5,075) = 29,16кН

Тогда

N₅ = (26,64 – 1,941 • 0,95 • 4,384) • Sin 14 + 29,16 • Cos 14 = 32,78кН

Расчетная ось рамы u – u не совпадает с ее центральной осью z – z. Продольную силу N и изгибающий момент М_w, определенные относительно расчетной оси, следует перенести на центральную ось и учесть дополнительный изгибающий момент, относительно главной центральной оси Х сечения от переноса продольной силы.

Расстояние от расчетной оси рамы u – u до ее центральной оси z – z составляет:

е₁ = 0,5 • h₁ – h₀ = 0,5 • 752 – 217 = 159мм -для сечения высотой h₁=752 мм

e₂ = 0,5 • h₂ – h₀ = 0,5 • 384 – 217 = 25мм -для сечения высотой h₂ = 384 мм

Расчетный изгибающий момент относительно главной центральной оси сечения Х с учетом дополнительного момента от переноса продольной силы:

в сечении №2: М_х2 = М_w2 – N₂•е₁ = 113,33 – 76,4•0,159 = 101,18 кНм

в сечении № 5: М_х5 = М_w5 + N₅•e₂ = 26,18 + 32,78•0,025 = 27 кНм

Расчетную длину в плоскости рамы принимаем равной длине полурамы по расчетной оси СНиП “Нормы проектирования. Деревянные конструкции” п. 6.28: l_0x = l _пр = 1018, 8 см.

Гибкость рамы, соответствующая сечению с максимальными размерами СНиП “Нормы проектирования. Деревянные конструкции”, п.4.8:

l_х = l_0x/r_x = l_0x/(0,289•h₁) = 1018,8/(0,289•75,2) = 46,8

Коэффициент продольного изгиба СНиП “Нормы проектирования. Деревянные конструкции.”, п. 4.17, прим. 1 j_x = А/l_x² = 3000/46,8² = 1,36

Для элементов переменного по высоте сечения коэффициент j_x следует умножать на коэффициент k_жN (СНиП “Нормы проектирования. Деревянные конструкции”, п. 4.17, прим. 4). СНиП П-25-80 не позволяет определить значение k_жN для элементов со ступенчатым изменением высоты сечения. Поэтому коэффициент k_жNx проектируемой рамы вычисляем с помощью приложения 3, таблицы 1 методического пособия, составленной в развитие норм СНиП “Нормы проектирования. Деревянные конструкции.” При этом имеющую криволинейный участок полураму условно рассматриваем как прямолинейный элемент ступенчато-переменного сечения шарнирно опертый по концам.

Определим геометрические параметры полурамы a_ж и b (прил.3,табл. 1):

a_ж = l₁ / l = 6820/10188 = 0,66

где: l₁= 810 + 4024 + (5354 – 3000 – 736/2) = 6820 мм - длина по расчетной оси участка полурамы с большей высотой сечения (h₁), принимаемая равной от опорного сечения № 0 до средней части участка изменения высоты сечения;

1 = 1_пр = 10188 мм; b = h₂ /h₁ = 384/752 = 0,51

При a = 0,66 и b = 0,51 по табл. 1, прил. 3 методом интерполяции вычисляем k_жNx = 0,715

Проверка прочности по сечению № 2. Геометрические характеристики сечения №2: площадь брутто: F₁ = b•h₁ = 13,5•75,2 = 1015 см²; момент сопротивления брутто относительно главной оси сечения X, W_х1 = b•h₁²/6 = 13,5•75,2²/6 = 12723 см³

Сечение № 2 находится на криволинейном участке рамы. В соответствии с п. 6.30 СНиП “Нормы проектирования. Деревянные конструкции.”, при отношении: h₁/r = 752/2876 = 0,26 > 1/7, расчетный момент сопротивления сечения W_хследует умножать на коэффициент:

 при проверке напряжений по внутренней кромке:

k_rв =(1–0,5•h₁/r)/(1–0,17•h₁/r) =(1–0,5•752/2876)/(1–0,17•752/2876) = 0,9

при проверке напряжений по наружной кромке:

k_rн =(1+0,5•h₁/r)/(1+0,17•h₁/r) = (1+0,5•752/2876)/(1+0,17•752/2876)=1,12

Расчетное сопротивление древесины сосны 2 сорта с учетом коэффициентов условий работы по СНиП “Нормы проектирования. Деревянные конструкции”, п. п. 3.1, 3.2.:

а) сжатие вдоль волокон R_с = 15•m_в•m_т•m_б•m_сл•m_гн (МПа),

здесь m_в = 1 - для условий эксплуатации Б2

m_т = 1 – для температуры эксплуатации до +35°С

m_б = 0,9225 – при h₁ = 75,2 см

m_сл = 1,15 – при толщине слоя d = 16 мм

m_гн = 0,812 – при r_к/а = r_в/d = 156

тогда R_с = 15•1•1•0,9225•1,15•0,812 = 12,92 МПа

б) растяжение вдоль волокон R_р = 9•m_в•m_т•m_гн (МПа)

здесь m_в = 1; m_т = 1; m_гн = 0,710 - при r_к /а = r_н /d = 3252/16= 203

тогда R_р = 9•1•1•0,710 = 6,39 МПа

В соответствии со СНиП “Нормы проектирования. Деревянные конструкции”, п.4.17, прим.1, находим:

x = 1–N₂/(j_x•k_жNx•R_c•F_бр) = 1 – 76,4/(1,36•0,715•12,6•10³•1015•10^-4) = 0,94

(F_бр = F₁ = 1015 см²);

М_д2 = М_х2 /x = 101,18/0,94 = 107,6 кНм

Расчет прочности сечения № 2 рамы производим по формуле (28) п. 4.17, с учетом требований п. 6.30 СНиП “Нормы проектирования. Деревянные конструкции”:

проверка напряжений до сжатой внутренней кромке:

s_в = N₂/F_расч + М_д2 /(W_расч•k_rв) = 76,4/1015•10^-4 + 107,6/(12723•10^-6•0,9) = 10150 кПа = 10,15 МПа < R_с = 12,92 МПа

проверка напряжений по растянутой наружной кромке:

s_н=N₂/F_расч–М_д2 /(W_расч•k_rн)=76,4/1015•10^-4–107,6/(12723•10^-6•1,12)=6 МПа < R_p = 6,39 МПа

где F_расч = F₁ = 1015 см²; W_расч = W_х1 = 12723 см³

Прочность рамы по сечению №2 обеспечена.

Проверка прочности по сечению № 5. Ггеометрические характеристики сечения №5: площадь брутто: F₂ = b×h₂ = 13,5×38,4 = 518см²; момент сопротивления брутто относительно главной оси сечения X: W_x2 = b×h₂²/6 = 13,5×38,4²/6 = 3318 см³.

Расчетное сопротивление древесины сосны 2 сорта при сжатии вдоль волокон СНиП II-25-80 “Нормы проектирования. Деревянные конструкции”, п.п. 3.1, 3.2:

R_c = 15×m_в×m_т×m_б×m_сл (МПа).

Имеем m_в = 1 СНиП “Нормы проектирования. Деревянные конструкции.”, п. 3.2.а;

m_т = 1 СНиП “Нормы проектирования. Деревянные конструкции.”, п. 3.2.6;

m_б = 1 – при h₂ = 38,4 см;

m_сл = 1,15 – при толщине слоя d = 16мм.

тогда R_с = 15×1×1×1×1,15 = 17,25 МПа;

В соответствии с СНиП “Нормы проектирования. Деревянные конструкции.”, п. 4.17, прим.1 находим:

x = 1 – N₅ /(j_x×k_жNx×R_c×F_макс) = 1 – 32,78/(1,36×0,715×17,25×10³×1015×10^-4) = 0,980;

здесь значения j_х, k_жNx, R_c, F_макс приняты для максимального по высоте сечения № 2, СНиП “Нормы проектирования. Деревянные конструкции.”, п. п. 4.8, 4.17 прим. 4;

М_д5 = М_х5 /x = 25/0,980 = 25,51 кН×м.

Расчет прочности сечения № 5 рамы производим по формуле (28) п. 4.17 СНиП “Нормы проектирования. Деревянные конструкции.”

s = N₅ /F_расч + М_{д 5} /W_расч = 32,78/518×10^-4 + 25,51/3318×10^-6 = 7,75 МПа < R_с = 17,25 МПа;

где F_расч = F₂ = 518см²; W_расч = W_х2 = 3318см³.

Прочность рамы по сечению № 5 обеспечена.

7.2.Расчет рамы на устойчивость плоской формы деформирования

Устойчивость плоской формы деформирования рамы проверяем в соответствии с указаниями п. 6.29 СНиП “Нормы проектирования. Деревянные конструкции.”

Закрепление рам из их плоскости обеспечивают прогоны и продольные вертикальные связи. Каждая полурама между опорным сечением № 0 и коньковым - №8 раскреплена из плоскости деформирования прогонами на участке ригеля и продольными вертикальными связями (балка с волнистой стенкой) - на криволинейном участке в сечении № 2. Прогоны раскрепляют наружную кромку полурамы, а продольные связи - наружную и внутреннюю.

Участки полурамы между сечениями, раскрепленными по наружной и внутренней кромкам, обозначим:

участок 0 – 2, длиной l₀₂ = 2822 мм - между сечениями № 0 и № 2;

участок 2 – 8, длиной l₂₈ = 7366 мм - между сечениями № 2 и № 8.(см.рис.7,а).

Потеря устойчивости плоской формы деформирования рамы может наступить как в случае действия максимального отрицательного, так и положительного изгибающего момента. Анализ ординат эпюр расчетных изгибающих моментов в раме (табл. 3) и условий ее раскрепления из плоскости изгиба позволяет установить необходимость выполнения двух проверок устойчивости. Первая проверка - на участке 0 – 2 при действии максимального изгибающего момента в сечении № 2 М_w2 = 113,33 кН×м.(табл.3) (см. рис.7,в). Вторая проверка - на участке 0 – 8 при действии максимального изгибающего момента в сечении № 2 М_w2 = 76,17 кН×м (табл.3), (см. рис.7,в).

Проверка устойчивости на участке 0 - 2

Расчетные усилия в сечении № 2 относительно главной оси сечения х – х (см. выше)

N₂ = 76,4 кН, М_х2 = 101,18 кН×м. (при М_w2 = 113,33кН×м);

Расстояние между точками закрепления рамы от смещения из плоскости изгиба:

l_р = l₀₂ = 282,2см СНиП “Нормы проектирования. Деревянные конструкции.”, п. 4.14.

Гибкость участка 0 – 2 рамы из плоскости деформирования:

l_у = l_р /r_у = l_р /(0,289×b) = 282,2/(0,289×13,5) = 72,3

Коэффициент продольного изгиба для гибкости из плоскости деформирования:

j_у = 3000/l_у² = 3000/72,3² = 0,57

Коэффициент j_м определяем по формуле (23) СНиП “Нормы проектирования. Деревянные конструкции.” с введением в знаменатель правой части коэффициента m_б.

Значение m_б = 0,915 получено для сечения высотой h₁ = 752 мм.

j_м = 140×[b²/(l_p×h₁ ×m_б)]×k_ф = 140×[13,5²/(282,2×75,2×0,915)]×1,75 = 2,29, где коэффициент k_ф, определен по табл. 2 прил. 4 СНиП “Нормы проектирования. Деревянные конструкции.” при треугольной форме эпюры изгибающих моментов на участке 0 – 2, отношение концевых моментов a = 0, которой заменена действительная эпюра (см.рис.7,г).

Имеем k_ф = 1,75 – 0,75×a = 1,75 – 0,75×0 = 1,75.

Согласно СНиП “Нормы проектирования. Деревянные конструкции.”, п. 4.18 к коэффициенту j_у вводим коэффициенты k_пN и k_жNy, а к коэффициенту j_м - коэффициенты k_пм и k_жм .

Рама на участке 0 – 2 не имеет промежуточных закреплений из плоскости деформирования по растянутой от момента кромке (см.рис.7,а). (m = 0 – число закреплений). Тогда k_пN =1 и k_пм = 1 (см. формулы (34) и (24) СНиП “Нормы проектирования. Деревянные конструкции.”).

Высота сечения рамы по длине участка 0 – 2 постоянна (срез на опоре не учитываем), тогда k_жNy = 1 и k_жм = 1 “Пособие по проектированию деревянных конструкций”, п. 4.24.

Расчетное сопротивление древесины сосны 2 сорта при сжатии и изгибе вдоль волокон для сечения № 2 рамы “Нормы проектирования. Деревянные конструкции.” п.п. 3.1, 3.2: R_с = R_и = 15×m_в×m_т×m_б×m_сл×m_гн = 15×1×1×0,915×1,15×0,870 = 13,73 МПа,

здесь m_в = 1; m_т = 1; m_б = 0,915; m_сл = 1,15 - определены для сечения № 2 выше; m_гн = 0,870 определен по табл. 9 СНиП “Нормы проектирования. Деревянные конструкции.”

при r_к /а = r_p/d = 3035/16 = 190, для радиуса кривизны r_p расчетной оси рамы.

Находим по СНиП “Нормы проектирования. Деревянные конструкции., п. 4.17, прим. 1:

x = 1 – N₂ /(j_x×k_жNx×R_c×F_бр) = 1 – 76,4/(1,36×0,715×13,73×10³×1015×10^-4) = 0,943;

где j_x×k_жNx = 1,36×0,715 получены для сечения № 2 см.выше; F_бр = F₁ = 1015 см²,

М_д2 = М_х2 /x = 101,18/0,943 = 107,29 кН×м.

Подставив найденные значения в формулу (33) СНиП “Нормы проектирования. Деревянные конструкции”, получим:

N₂ /(j_y×k_пN×k_жNy×R_c×F_бр) + [М_д2 /(j_м ×k_пм ×k_жм ×R_и ×W_бр)]ⁿ = 76,4/(0,57×1×1×13,73×10³×1015×10^-4) + [107,29/(2,29×1×1×13,73×10³×12723×10^-6)]² = 0,096+0,072 = 0,168 < 1,

где n = 2 – т. к. нет закрепления растянутой зоны из плоскости деформирования;

F_бр = F₁ = 1015см²; W_бр = W_х1 = 12723см³.

Устойчивость плоской формы деформирования рамы на участке 0 – 2 обеспечена.

Проверка устойчивости на участке 2 – 8

Расчетный изгибающий момент в сечении № 2 относительно оси w – w при действии на раму постоянной и снеговой односторонней справа нагрузках М_w2 = 76,17 кН×м. Значение расчетной продольной силы, действующей по расчетной оси рамы в сечении № 2 при таком же сочетании нагрузок, как и для момента М_w2 = 76,17 кН×м, найдем по формуле:

N₂ = (R_A - q g_n x₂) Sin (ψ/2) + H_A Cos (ψ/2) =

= (26,64 – 1,843·0,637) Sin (104°/2) + 29,16Cos (104°/2) = 38,02 кН

Где значения R_A= 26,64кН и Н_A = 29,16кН найдены выше

Продольную силу N₂ перенесем с расчетной оси рамы на ее центральную ось. Тогда расчетный изгибающий момент в сечении № 2 относительно главной центральной оси

х – х с учетом дополнительного момента от переноса продольной силы:

М_х2 = М_w2 – N₂×e₁ = 76,17 – 76,4×0,159 = 64,02 кН×м.

На участке 2 – 8 изгибающий момент растягивает наружную кромку рамы. Расстояние между точками закрепления сжатой внутренней кромки рамы от смещения из плоскости изгиба l_р = l₂₈ = 736,6 см (см.рис.7,а).

Гибкость участка 0 – 8 рамы из плоскости деформирования:

l_у = l_р /r_у = l_р /(0,289×b) = 736,6/(0,289×13,5) = 189

Коэффициент продольного изгиба для гибкости из плоскости деформирования:

j_у = 3000/l_у² = 3000/189² = 0,084 по СНиП “Нормы проектирования. Деревянные конструкции.”, п. 4.18).

 Коэффициент j_м определяем по формуле (23) СНиП “Нормы проектирования. Деревянные конструкции.” с учетом указаний п.4.25 “Пособие по проектированию деревянных конструкций”.

j_м= 140×[b²/(l_p×h₁ ×m_б)]×k_ф = 140×[13,5²/(736,6×75,2×0,915)]×1,5 = 0,755,

где h₁ = 752 мм – максимальная высота поперечного сечения на участке l_p,

m_б = 0,915 - получен для сечения высотой 752 мм выше;

коэффициент k_ф, определен по табл. 2 прил. 4 СНиП “Нормы проектирования. Деревянные конструкции.” при треугольной форме эпюры изгибающих моментов, которой заменена действительная эпюра с учетом закрепления на участке 2 – 8 по концам и растянутой от момента М кромке, отношение концевых моментов a = 0, тогда

k_ф = 3/(2 + a) = 3/(2 + 0) = 1,5.

К коэффициентам j_у и j_м следует ввести коэффициенты k_пN х k_жNy, и k_пм х k_жм соответственно согласно СНиП “Нормы проектирования. Деревянные конструкции.”, п. 4.18. По формулам (34) и (24) СНиП “Нормы проектирования. Деревянные конструкции.” имеем:

k_пN = 1 + [0,75 + 0,06×(l_p /h₁)² + 0,6×a_p×(l_p /h₁) – 1]×m² /(m² + 1);

k_пм = 1 + [0,142×(l_p /h₁) + 1,76×(h₁ /l_p) + 1,4×a_p – 1]×m² /(m² + 1);

Центральный угол, определяющий участок расчетной длины кругового очертания (между сечениями № 2 и № 3) по радиусу кривизны расчетной оси,

a_p = j/2 = 76°/2 = 0,663 рад

Фактическое число промежуточных подкрепленных точек растянутой кромки на участке 2 – 8 равно четырем. Расчетная модель элементов, использованная при выводе формул СНиП П-25-80 для расчета на устойчивость плоской формы деформирования, предусматривает, что дискретные промежуточные подкрепления растянутой или менее напряженной кромки элемента идут на участке l_р с одинаковым шагом “Пособие по проектированию деревянных конструкций”. Для приближения фактического раскрепления наружной кромки на участке 2 – 8 к идеализированной расчетной модели подкрепляющее действие второго от конькового узла прогона не учитываем.

Число промежуточных подкрепленных точек принимаем m = 2. Находим:

k_пN = 1 + [0,75 + 0,06×(736,6/75,2)² + 0,6×0,663×(736,6/75,2) – 1]×2² /(2² + 1) = 8,52

k_пм = 1 + [0,142×(736,6/75,2) + 1,76×(75,2/736,6) + 1,4×0,663 – 1]×2² /(2² + 1) = 2,19;

Коэффициенты k_жNy и k_жМ проектируемой рамы вычисляем с помощью табл. 1 и 2 прил. 3 методического пособия, составленных в развитие норм СНиП “Нормы проектирования. Деревянные конструкции”.

При определении k_жNy участок 2 – 8 условно рассматриваем как прямолинейный элемент ступенчато-переменного сечения. Геометрические параметры по табл.1, прил.3 методического пособия:

a_ж = l₁/l₂₈ = 4366/7366 = 0,538; b = h₂ /h₁ = 384/752 = 0,510

По табл. 1 прил. 3 методического пособия методом интерполяции вычисляем k_жNy = 0,884.

При определении k_жм участок 2 – 8 условно рассматриваем как прямолинейный элемент с линейно изменяющейся высотой сечения от h₁ = 752 мм до h₂ = 384 мм. Тогда для условно принятой треугольной формы эпюры моментов, a = 0 и b = h₂ /h₁ = 0,510 по табл.2, прил. 3 методического пособия получим:

k_жм = b^{1/ (3,5 – 1,4×a)} = 0,510^{1/ (3,5 – 1,4×0)} = 0,825

По СНиП “Нормы проектирования. Деревянные конструкции.”, п. 4.17, прим. 1 находим:

x = 1 – N₂/(j_x×k_жNx×R_c×F_бр) = 1 – 76,4/(1,36×0,715×13,73×10³×1015×10^-4) = 0,943;

где j_x, k_жNx, R_c, F_бр то же что для сечения № 2 выше;

М_д2 = М_х2 /x = 101,18/0,943 = 107,29 кН×м.

Подставив найденные значения в формулу (33) СНиП “Нормы проектирования. Деревянные конструкции.”, получим:

N₂ /(j_y×k_пN×k_жNy×R_c×F_бр) + (М_д2 /(j_м ×k_пм ×k_жм ×R_и ×W_бр))ⁿ = 76,4/(0,084×8,52×0,884×13,73×10³×1015×10^-4) + (107,29/(0,755×2,19×0,825×13,73×10³×12723×10^-6))¹ = 0,539 < 1,

где n = 1 - т. к. растянутая зона раскреплена из плоскости деформирования.

Устойчивость плоской формы деформирования рамы на участке 2 – 8 обеспечена.

8.Конструирование и расчет узлов рамы

Коньковый узел. Соединение полурам в коньковом узле предусматриваем упором торцов, срезанных по наружной кромке под углом на 50 мм для большей шарнирности узла и предотвращения откола крайних волокон при повороте элементов узла. Концы полурам перекрывают парные клееные деревянные накладки на болтах, обеспечивающие восприятие поперечной силы при односторонней нагрузке на рамы и поперечную жесткость узла из плоскости.

Торцы полурам в коньковом узле подвержены сминающему действию горизонтальной силы. Максимальная величина горизонтальной силы в сечении № 8 соответствует воздействию на раму постоянной и снеговой нагрузок на всем пролете.

N₈ = H_A = (q g_n + p g_n) l ²/(8 f) = 48 кН (см.выше)

Площадь смятия торцов полурамы в узле(см.рис.2):

F_см = 13,5×34,6 = 467,10 см²

Смятие происходит под углом a = 14° к волокнам. Расчетное сопротивление древесины смятию СНиП “Нормы проектирования. Деревянные конструкции.”, п. 3.1, табл.3,прим. 2:

R_{cм. 14} = R_cм ×m_в ×m_т /[1 + (R_см / R_cм.90 –1) Sin³ 14°] =

= 11×1×1/[1 + (11/3 – 1)×Sin³ 14°] = 10,6 МПа

где R_см = 11 МПа - принято для древесины 3 сорта.

Расчетная несущая способность соединения из условия смятия древесины:

Т = R_{см. 14} ×F_см = 10,6×10³ ×467,10×10^-4 = 495,13 кН > N₈ = 48 кН

Прочность торца полурамы на смятие обеспечена.

Расчетная поперечная сила в коньковом узле (сечение № 8) при загружении рамы односторонней снеговой нагрузкой р×g_n = 6,84 кН/м на половине пролета(см.рис.5) будет:

Q₈ = р×g_n×l / 8 = 6,84×15/8 = 12,8 кН

Поперечную силу Q₈ воспринимают клееные деревянные накладки и стальные болты. Накладки принимаем шириной сечения b_н = 90 мм, склеенными из пакета досок сечением после фрезеровки 35 х 90 мм (сечение заготовок 40 х 100 мм - по сортаменту пиломатериалов ГОСТ 24454-80Е; припуски на фрезеровку заготовок по пласти и пакета по боковым поверхностям приняты в соответствии с руководством по изготовлению и контролю качества деревянных клееных конструкций). Высоту сечения накладок h_н и их длину l_н определим далее, исходя из требований по расстановке болтов. Болты принимаем диаметром d = 20 мм.

 

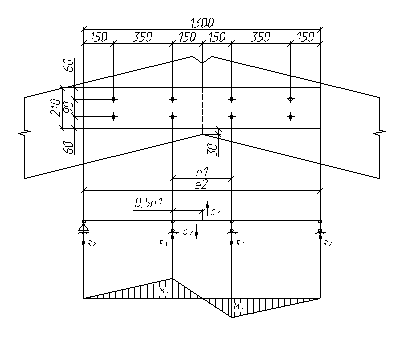
Рис.8 Коньковый узел рамы

а – конструкция узла; б –эпюра изгибающих моментов в накладках.

Накладки работают как многопролетные неразрезные балки на поперечный изгиб. Опоры накладок – болты. Расстояния между болтами вдоль волокон древесины накладки, с учетом требований п. 5.18 СНиП “Нормы проектирования. Деревянные конструкции.”, назначаем е₁ = 300 мм, е₂ = 1000 мм (см. рис.8,а).

Усилия R₁, R₂, действующие на болты, определим, учитывая кососимметричную схему работы накладок и прикладывая к ним поперечную силу Q₈ в точке перегиба их оси:

R₁ = Q₈ /(1 – e₁ /e₂) = 12,8/(1 – 0,3/1) = 18,2 кН

R₂ = Q₈ /(e₂ /e₁ – 1) = 12,8/(1/0,3 – 1) = 5,5 кН

Максимальный изгибающий момент в накладках: М_н = Q₈×е₁ /2 = 12,8×0,3/2 = 1,92 кН×м (см. рис.8,в).

Расчетная несущая способность болта на один шов сплачивания при направлении передаваемого усилия под углом 90° для накладок в соответствии с п.п.5.13, 5.14 СНиП “Нормы проектирования Деревянные конструкции.”:

из условия изгиба болта:

T_u = (1,8×d² + 0,02×a²)×= (1,8×2² + 0,02×13,5²)×= 8,04 кН

T_u^I = 2,5×d² = 2,5×2²= 7,42 кН

из условия смятия среднего элемента – рамы:

Т_c = 0,5×с×d×k_a = 0,5×13,5×2×0,55 = 7,42 кН

из условия смятия крайнего элемента – накладки:

Т_a = 0,8×a×d×k_a = 0,8×9×2×0,55 = 7,92 кН

где с = b = 13,5 см; а = b_н = 9 см; k_a = 0,55 – по таблице 19 СНиП “Нормы проектирования. Деревянные конструкции.” при a = 90°.

Наименьшая расчетная несущая способность Т = T_u^I = Т_u = 7,42 кН

Необходимое число болтов в ближайшем к узлу ряду СНиП “Нормы проектирования. Деревянные конструкции.”, табл. 17, прим. 7 :

n_б1 = R₁ /(Т×n_ш) = 18,2/(7,42×2) = 1,22

где n_ш = 2 - число расчетных швов одного болта. Принимаем два болта.

Необходимое число болтов в дальнем от узла ряду:

n_б2 = R₂ /(Т×n_ш) = 5,5/(7,42×2) = 0,37

Достаточно поставить один болт. Конструктивно для обжатия накладок ставим два болта.

Окончательная вертикальная и горизонтальная расстановка болтов относительно накладки и конькового торца полурам выполнена исходя из требований п. 5.18 СНиП “Нормы проектирования. Деревянные конструкции.”(см.рис. 8,а)

Высоту накладок с учетом вертикальной расстановки болтов принимаем h_н = 210 мм, из шести слоев досок толщиной 35 мм, длину накладок с учетом горизонтальной расстановки болтов принимаем l_н = 1300 мм.

Момент сопротивления накладки, ослабленной в расчетном сечении двумя отверстиями диаметром 20 мм:

W_нт.н = W_бр.н - W_осл = 9×21² /6-(9×2×4/6+9×2²/6)= 680 см³

Напряжения в накладках от изгиба:

s_н = M_н /(n_н ×W_нт.н) = 1,92/(2×680×10^-6) = 1412 кПa = 1,4 MПa < R_и = 12,86 MПa,

где n_н = 2 - число накладок

 R_и = 13×m_в×m_т×m_сл = 13×1×1×0,989 = 12,86 МПа (по СНиП “Нормы проектирования. Деревянные конструкции”, п. п. 3.1, 3.2)

m_сл = 0,989 – при толщине слоя 35 мм.

Прочность накладок обеспечена.

Опорный узел (пятовой шарнир)

Опирание рамы решаем продольным лобовым упором торца и поперечным лобовым упором наружной кромки опорного конца полурам в стальной башмак. Башмак воспринимает опорные реакции рамы и передает их на бетонный фундамент. Для обеспечения большей шарнирности узла и уменьшения площади контакта рамы с башмаком опорный торец полурамы срезан под углом со стороны внутренней кромки.

Древесину рамы для предотвращения ее конденсационного увлажнения отделяем от стальных поверхностей башмака оклеечной гидроизоляцией из изола марки И-БД (ГОСТ 10296-79).

Опорный конец полурамы скрепляем с башмаком конструктивным болтом класса точности В (нормальная точность) диаметром , d_b = 20 мм. Башмак к фундаменту крепим двумя расчетными анкерными болтами класса точности В класса прочности 4,6. Диаметр анкерных болтов предварительно назначаем d_ba = 24 мм. Для города Кургана расчетная температура t = –38°С по СНиП 2.01.01 - 82. “Строительная климатология и геофизика”. Марку стали анкерных и конструктивных болтов при t = –37°С, в соответствии с указаниями «Пособия по проектированию стальных конструкций», назначаем ВстЗкп2 по ГОСТ 535-88.

Башмак проектируем сварным, состоящим из горизонтальной опорной плиты с проушинами для анкерных болтов, двух вертикальных щек с отверстиями для крепежного болта и вертикальной упорной диафрагмы. Материал для изготовления элементов башмака – листовая прокатная широкополосная универсальная сталь (ГОСТ 82-70*). Сталь проката - С245, по ГОСТ 27772-88. Выбор стали произведен по табл. 50* СНиП “Нормы проектирования. Стальные конструкции” для конструкции группы 3 и расчетной температуре t = –37°С по СНиП 2.01.01- 82, “Строительная климатология и геофизика”.

Фундамент выполняем из бетона класса В12,5 согласно “Руководству по проектированию фундаментов на естественном основании под колонны зданий и сооружений”.

Расчет опорного узла производим на восприятие наибольших опорных реакций рамы, соответствующих воздействию на раму постоянной и снеговой нагрузки на всем пролете. Расчетные усилия на опоре (определены выше):

вертикальная реакция: R_A = 65 кН

распор: Н_A = 48 кН

Опорный конец полурамы в пяте (сечение № 1) проверяем на прочность:

- по скалыванию клеевого шва силой Q = Н_A = 48 кН в соответствии с формулой (18) СНиП “Нормы проектирования. Деревянные конструкции.”, преобразованной путем замены S_бр и I_бр их выражениями для прямоугольного сечения к виду:

t_ск = 1,5 Q/(h₀×b_расч) = 1,5×48×10^-3 /(0,6 ×0,135) = 0,88 МПа < R_ск = 1,72МПа;

где h₀ = 600 мм высота сечения рамы в пяте (см.рис.2); b_расч = b =135 мм;

R_ск = 1,5 m_в× m_т ×m_сл = 1,5×1×1×1,15 = 1,72 МПа – для древесины 3 сорта(СНиП “Нормы проектирования. Деревянные конструкции.”, п. п. 3.1, 3.2);; m_сл = 1,15

- по смятию вдоль волокон древесины торцовой поверхности силой R_A = 65 кН в соответствии с формулой (52) СНиП “Нормы проектирования. Деревянные конструкции”:

s_см = R_A/F_см = R_A/(h₀×b_расч) = 65×10^-3 /(0,6×0,135) = 0,82 МПа < R_см = 11 МПа,

R_см = 11×m_в×m_т = 11×1×1 = 11 МПа - для древесины 3 сорта (СНиП “Нормы проектирования. Деревянные конструкции.” п. п. 3.1, 3.2).

Вертикальная упорная диафрагма башмака воспринимает нагрузку от давления распора рамы Н_А, передаваемого поперечным лобовым упором наружной кромки опорного конца полурамы (см.рис.10). Высоту упорной диафрагмы h_уд определим из условия смятия древесины поперек волокон. Минимально необходимая высота:

h_уд.min = H_A/(b×R_см.90) = 48/(0,135×3×10³) = 0,118 м =118 мм,

где R_см.90 = 3×m_в×m_т = 3×1×1 = 3 МПа (СНиП “Нормы проектирования. Деревянные конструкции”, табл. 3, п. 4.а).

Принимаем h_уд = 120 мм (ширина проката по ГОСТ 82-70*).

Толщину упорной диафрагмы d_уд находим из условия работы ее на изгиб как балки пролетом l_уд = 140 мм, опертой на щеки башмака, под действием равномерной нагрузки g_уд = Н_А/l_уд от давления распора Н_А. Размер l_уд = 140 мм принят, исходя из ширины сечения рамы b = 135 мм, плюс 5 мм на зазор между опорным концом полурамы и щеками башмака. Зазор обеспечивает прокладку гидроизоляции и свободную установку рамы в башмак.

Изгибающий момент в упорной диафрагме, без учета частичного защемления сварным швом диафрагмы на опорах (щеках), найдем по формуле:

М_уд = d_уд×l_уд² /8 = H_A×l_уд /8 = 48×0,14/8 = 0,84 кН×м.

Требуемый момент сопротивления диафрагмы:

W_уд.тр = М_уд /(R_y.g_c) = [0,84/(240×10³×1)]×10⁶ = 3,5 см³

где R_у = 240 МПа - расчетное сопротивление стали С245; g_с = 1 - коэффициент условий работы по СНиП “Нормы проектирования. Стальные конструкции”, табл. 6*, прим. 4.

Минимально необходимая толщина диафрагмы:

d_уд.min = 1,32 см

Принимаем d_уд.min = 14 мм (толщина проката по ГОСТ 82-70*).

Упорная диафрагма через сварные угловые швы передает распор рамы Н_A = 48 кН на щеки башмака.

Щеки башмака назначаем толщиной d_щ = 10 мм, высотой h_щ. = 120 мм (размеры проката по ГОСТ 82-70*).

Под действием распора щеки работают на внецентренное растяжение. В соответствии с требованиями СНиП “Нормы проектирования. Стальные конструкции.”,п.5.25* проверяем прочность щек:

s = H_A/2×A_щ + М_Н/2×W_щ = 48/(2×12×10^-4) + 2,88/(2×24×10^-6) = 8000 кПа =

=80 МПа < R_y×g_с = 240 МПа

где М_Н = Н_А×h_уд /2 = 48×0,12/2 = 2,88 кН×м - момент, возникающий от опрокидывающего действия распора Н_А на башмак;

А_щ = h_щ×d_щ = 12×1 = 12 см² – расчетная площадь сечения;

W_щ = d_щ×h_щ²/6 = 1×12²/6 = 24 см³ – расчетный момент сопротивления;

R_у×g_c = 240×1 = 240 МПа - расчетное сопротивление стали С245 с учетом g_с = 1.

Прочность щек обеспечена.

Опорная плита башмака воспринимает вертикальные нагрузки R_A =65кН (вертикальная опорная реакция рамы) и М_Н = 2,88 кН×м (момент от опрокидывающего действия распора на башмак, см. выше), а также горизонтальную – распор Н_А = 48 кН. Под действием вертикальных нагрузок опорная плита, лежащая на железобетонном фундаменте, работает на изгиб как плита на упругом основании. Распор Н_А плита передает через шайбу (см.рис.9) на анкерные болты.

Длину опорной плиты конструктивно назначаем l_оп = 730 мм, ширину b_оп = 340 мм. Толщину опорной плиты d_оп найдем из условия работы плиты на изгиб. Изгибающие моменты в плите вычислим раздельно для нагрузок R_A и М_H и далее по наиболее неблагоприятной комбинации моментов определим d_оп.

Наряду с эпюрами изгибающих моментов в опорной плите, построим для нагрузок R_A и М_H эпюры реактивных давлений фундамента на плиту.

Построение эпюр реактивных давлений фундамента и изгибающих моментов в опорной плите башмака от нагрузки R_A. Принимаем, что нагрузка R_A передается полурамой на опорную плиту в виде вертикального сплошного давления по площади контакта:

q = R_A/(b×h₀) = 65/(0,135×0,6) = 802 кПа,(смюрис.10) где b и h₀ - размеры полурамы в пяте.

Опорную плиту можно рассчитать (в запас прочности) только в поперечном направлении (вдоль стороны b_оп) в условиях плоской задачи теории упругости. Для этого из опорной плиты в поперечном направлении выделяем полосу шириной b₁ = 1 см(см.рис.10,а, сеч. а-а) Полосу рассматриваем как балку на упругом основании, симметрично нагруженную в средней части равномерно распределенной нагрузкой q. Упругое основание (фундамент) работает в условиях плоской деформации, поэтому расчет балки можно выполнить методом, разработанным И.А. Симвулиди “Расчет инженерных конструкций на упругом основании”. Для расчета по этому методу нагрузку на балку необходимо задавать распределенной по площади, т.е. в нашем расчете q = 802 кПа.

Эпюры реактивных давлений фундамента р₁ и изгибающих моментов в балке М₁ построим с помощью приложения 5 методического пособия. Предварительно вычислим относительные абсциссы привязки распределенной нагрузки:

b_н = l_н /L = 102,5/340 = 0,3;

b_к = l_к /L = 237,5/340 = 0,7;

где l_н = 102,5 мм - расстояние от левого конца балки (полосы) до начала распределенной нагрузки q; l_к = 237,5 мм - расстояние от левого конца балки до конца распределенной нагрузки q; L = b_оп = 340 мм.

В соответствии с указанием прил. 5 методического пособия сначала рассмотрим балку, нагруженную нагрузкой q на правом конце на участке от х = l_н до х = l_к (х - абсцисса сечений балки), затем рассмотрим ту же балку, нагруженную нагрузкой q с обратным знаком на правом конце на участке от х = l_к до х = L.

Значения безразмерных ординат  и  вычислим в табличной форме (табл.4 и 5). Для этого из прил. 5, табл. 1 и 2 принимаем значения  и  от x = 0 до x = 1 (x = х/L - относительная абсцисса сечений балки) для нагрузки, расположенной на участке от х = l_н до х = L, т.е. при b = b_н = 0,3; и далее все значения  и  от x = 0 до x = 1 для нагрузки, расположенной на участке от х = l_к до х = L, т.е. при b = b_к = 0,7.

Используя принцип независимости действия сил, определим безразмерные ординаты  и  для фактической нагрузки q, вычитая из ординат  и  соответствующие ординаты  и .

Ординаты реактивных давлений р₁ и изгибающих моментов М₁ по длине балки, соответствующие фактическому значению нагрузки q = 802 кПа получаем по формулам

p₁ = ×q; M₁ = ×q×b₁×L²

Результаты расчета p₁ и М₁ приведены в последней строке табл. 4 и 5.

Вычисление ординат эпюры реактивных давлении фундамента p₁ = ×q = 820× (кПа)

Таблица 4

x	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
	-0,056	0,196	0,377	0,508	0,605	0,688	0,773	0,880	1,025	1,228	1,514
	-0,134	-0,057	-0,010	0,024	0,064	0,127	0,232	0,396	0,638	0,975	1,426
	0,078	0,253	0,387	0,484	0,541	0,561	0,541	0,484	0,387	0,253	0,088
p1 = ×q	64	207	317	397	444	460	444	397	317	207	72

Вычисление ординат эпюры изгибающих моментов в полосе шириной b₁ = 1 см

M₁ = ×q×b₁ ×L² =×820 ×0,01×0,34² = 0,945× = 945× (Н×м)

Таблица 5

x	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
	0	-0,001	0,002	0,008	0,013	0,016	0,014	0,011	0,006	0,002	0
	0	-0,001	-0,002	-0,003	-0,003	-0,004	-0,003	-0,002	-0,001	0,001	0
	0	0	0,004	0,011	0,016	0,02	0,017	0,013	0,007	0,001	0
M1 = ×q×b1×L2	0	0	3,78	10,40	15,12	18,9	16,07	12,29	6,62	0,95	0

Построение эпюр реактивных давлений фундамента и изгибающих моментов в опорной плите башмака от нагрузки М_Н = 2,88 кН×м. Щеки башмака через сварные угловые швы передают изгибающий момент М_Н = Н_А×h_уд /2 (см. выше) на опорную плиту (см.рис.9). Эпюра вертикального давления на опорную плиту от момента М_Н, в предположении упругих деформаций стали - треугольная на половине длины плиты (см.рис. 10,б). Максимальная величина линейного давления у края плиты от одной щеки:

q_щ = 0,5×М_Н /(l_оп² /6) = 0,5×2,88/(0,63² /6) = 12,77 кН/м

Расчет опорной плиты выполним в условиях плоской задачи, выделив из плиты в поперечном направлении полосу шириной b₁ = 1 см от края (см.рис.10,б, вид б-б). Полосу рассматриваем как балку на упругом основании, симметрично нагруженную сосредоточенными силами

Р = q_щ ×b₁ = 12,77×0,01 = 0,128 кН, на расстоянии а = 95 мм от продольного края плиты. Точки приложения сил Р приняты по центру толщины щек. Длина балки L = b_оп = 340мм.

Эпюру реактивных давлений фундамента p₂ на балку (полосу) с достаточной для инженерного расчета точностью можно принять равномерной по длине балки L. Тогда величину реактивного давления фундамента р₂ вычислим по формуле:

p₂ = 2×Р/(b₁×L) = 2×0,128/(0,01×0,34) = 75 кПа (см.рис.10,б)

Балка работает на изгиб как двухконсольная, опертая на щеки башмака (опорные реакции Р=0,128 кН), нагруженная снизу реактивным давлением фундамента. Изгибающие моменты в балке M₂ определим, используя симметрию, только для левой половины в сечениях x = 0; 0,1; 0,2; 0,3; 0,4; 0,5 (x = х/L) и в сечении x = а/L = 0,095/0,34 = 0,279, под силой Р.

Для сечений x от 0 до 0,279:

момент M₂ = p₂ ×b₁×(x×L)² /2 = 75×10³×0,01×(x×0,34)² /2 = 43 x²:

при x = 0, M₂ = 0;

при x = 0,1, М₂ = 43×0,1² = 0,43 Н×м;

при x = 0,2, M₂ = 43×0,2² = 1,72 Н×м;

при x = 0,279, M₂ = 43×0,279² = 3,35 Н×м.

Для сечений x от 0,3 до 0,5:

момент M₂ = p₂ ×b₁×(x×L)² /2 – P×(x×L – a) = 75×10³×0,01×(x×0,34)² /2 – 0,128×10³×(x×0,34 – 0,095) = 43×x² – 128×(0,34×x – 0,095):

при x = 0,3, M₂ = 43×0,3² – 128×(0,34×0,3 – 0,095) = 2,97 Н×м;

при x = 0,4, M₂ = 43×0,4² – 128×(0,34×0,4 – 0,095) = 1,63 Н×м;

при x = 0,5, M₂ = 43×0,5² – 128×(0,34×0,5 – 0,095) = 1,15 Н×м;

В целях упрощения расчета условно считаем эпюры моментов М₁ и М₂ совмещенными в одном сечении опорной плиты (точнее полосе шириной b₁ = 1 см). В действительности моменты М₁ действуют, на расстоянии 30 мм от края плиты, а моменты M₂, по краю плиты. Ординаты эпюры изгибающих моментов М = М₁ + М₂, (расчетная комбинация), вычислены в табл. 6.

Расчетная комбинация изгибающих моментов в плите М = M₁ + M₂ (Н×м)

Таблица 6

x	0	0,1	0,2	0,279	0,3	0,4	0,5	0,6	0,7	0,721	0,8	0,9	1,0
M1	0	0	3,78	8,75	10,40	15,12	18,9	16,07	12,29	10,8	6,62	0,95	0
M2	0	0,43	1,72	3,35	2,92	1,63	1,15	2,04	2,92	3,35	1,72	0,43	0
M	0	0,43	5,50	12,10	13,32	16,75	20,05	18,11	15,21	14,15	8,34	1,38	0

Минимально необходимую толщину опорной плиты d_оп.min определим расчетом плиты по прочности на изгиб. Максимальный расчетный момент М = 20,05 Н×м (см. табл. 6). На основании формулы (28) СНиП “Нормы проектирования. Стальные конструкции”, заменив момент сопротивления его выражением для полосы шириной b₁ = 1 см, толщиной d_оп.min (W_min = b₁×d²_оп.min/6), найдем:

d_оп.min = = 0,0071 м = 7,1 мм,

где R_y = 240 МПа, g_c = 1 - см. выше.

Учитывая возможность отклонения в передаче давления нагрузкой R_A от принятого равномерного распределения по площади b×h₀ контакта торца полурамы с опорной плитой, что возможно из-за поворота опорного конца полурамы, толщину плиты следует назначить с запасом.

Принимаем d_оп = 10 мм (толщина проката по ГОСТ 82-70*).

Проверка бетона фундамента по прочности на сжатие

Напряжения сжатия в фундаменте s_b равны реактивным давлениям фундамента. В соответствии с эпюрами реактивных давлений (эпюры, как и ранее, условно считаем совмещенными в одном сечении) максимальное расчетное напряжение сжатия:

s_b = р₁ + p₂ = 460 +75 = 535 кПа – действует в середине ширины опорной плиты.

Имеем s_b = 0,535 МПа < R_b = 7,5 МПа, где R_b = 7,5 МПа - расчетное сопротивление бетона класса В12.5 осевому сжатию. Прочность бетона фундамента на сжатие обеспечена.

Проверка прочности анкерных болтов

Опорная плита башмака через приваренную к ней прямоугольную шайбу передает распор рамы Н_A = 48 кН на анкерные болты. Под действием распора анкерные болты работают на срез, шайба - на смятие.

Растягивающее усилие от момента М_H = 2,88 кН×м стремится оторвать опорную плиту башмака от фундамента. Отрыву препятствует вертикальная реакция рамы R_A = 65 кН, приложенная с эксцентриситетом е = 15 мм относительно центра продольной стороны опорной плиты. Если эпюра напряжений под опорной плитой от R_A и М_H имеет растянутую зону, то анкерные болты следует установить в центре тяжести растянутой зоны эпюры напряжений и необходимо проверить по прочности на растяжение. Выясним характер эпюры напряжений под опорной плитой, предполагая работу бетона фундамента по упругой стадии.

В соответствии с расчетной схемой рис.11,а, построим эпюры напряжений под опорной плитой от совместного действия нагрузок R_A и М_н (см.рис.11).

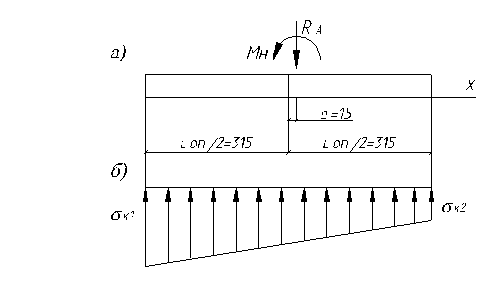
Рис.11. Определение характера суммарного напряженного состояния под опорной плитой

а - расчетная схема; б – эпюра напряжений под опорной плитой от совместного действия нагрузок R_а и М_н

Суммарные краевые напряжения под плитой (для напряжений сжатия принимаем знак «+»):

s_к1 = R_а /А_оп – R_A×е /W_оп + М_Н /W_оп = 65/0,214 – 65×0,015/0,03 + 2,88/0,03=367 кПа –сжатие

s_к2 = R_а /А_оп + R_A×е /W_оп – М_Н /W_оп=65/0,214 + 65×0,015/0,03 – 2,88/0,03=240 кПа – сжатие;

Суммарная эпюра напряжений под опорной плитой не имеет растянутой зоны, следовательно, отрыва плиты от фундамента не происходит, и анкерные болты на растяжение не работают.

Анкерные болты работают только на восприятие распора Н_A = 48 кН. Расчетное усилие, которое может быть воспринято одним анкерным болтом d_ba = 24 мм по СНиП “Нормы проектирования.Стальные конструкции.” п. 11.7*:

-           нa cpeз N_bs = R_bs×g_b×A_b×n_s = 150×10³×0,9×4,52×10^-4×1 = 61,0 кН;

-           на смятие N_bp = R_bp×g_b×d_ba×t_шб = 450×10³×0,9×0,024×0,008 = 77,8 кН,

где R_bs = 150 МПа - расчетное сопротивление срезу болта класса прочности 4.6 по СНиП “Нормы проектирования. Стальные конструкции.”, табл. 58*; R_bp = 450 МПа - расчетное сопротивление смятию элементов из стали с R_un = 370 МПа (R_un принято для стали шайб С245 по СНиП “Нормы проектирования. Стальные конструкции.”, табл. 51*), соединяемых болтами класса точности В; g_b = 0,9 - коэффициент условий работы болтового соединения, принят по табл. 35* СНиП “Нормы проектирования. Стальные конструкции.” для много-болтового соединения при болтах класса точности В; А_b = 4,52 см² – площадь сечения болта d_bа = 24 мм брутто по СНиП “Нормы проектирования. Стальные конструкции.” табл. 62*; n_s = 1 - число расчетных срезов одного болта; t_шб = 8 мм – наименьшая толщина элементов, сминаемых в одном направлении, равная толщине шайбы.

Проверяем прочность анкерных болтов:

-       на срез Н_А = 48 кН < n_b×N_bs×g_c = 2×61,0×1 = 122 кН

-       на смятие Н_A = 48 кН < n_b×N_bs×g_c = 2×77,8×1 = 156 кН

где n_b = 2 - количество болтов; g_c = 1 - в соответствии с СНиП “Нормы проектирования. Стальные конструкции.”, табл. 6*, прим. 4.

Прочность анкерных болтов обеспечена.

Проушины в опорной плите под анкерные болты выполним в центре стороны l_оп (см.рис.9).

Выбор типа анкерного болта и назначение глубины его заделки в фундамент производим в соответствии с рекомендациями “Руководства проектирования фундаментов на естественном основании под колонны зданий и сооружений”, п. 5.26. Принимаем болт с отгибом на конце.

Глубина заделки в фундамент l_а болта с отгибом должна быть 25 диаметров болта.

Тогда l_a = 25×d_ba = 25×24 = 600 мм (см.рис.9).

Заключение

В данной работе мы детально рассмотрели и рассчитали проект. Добавим, что деревянная архитектура имеет очень давнюю историю. Ей присуща с одной стороны, простота исходных геометрических форм, а с другой - богатство комбинаций, создаваемых использованием выразительной фактуры и текстуры дерева, декоративной резьбы и росписей. Применение новых материалов и технологий (антисептиков, антипиренов, прессование и склеивание древесины, использование плиты и объемных элементов из дерева и т.д.) сделало деревянную архитектуру актуальной и в современном строительстве. В настоящее время для постройки деревянных домов наиболее широко используют три конструктивные системы. - срубная (постройки выполнены из бревен-кругляка), - брусчатая (здания сооружают из брусьев прямоугольного сечения); - каркасная. Первые две системы получили распространение в странах Восточной и Северной Европы при строительстве домов, храмов, хозяйственных сооружений Каркасную систему - вертикальные столбы, горизонтальные ригели, раскосы - применяли в Европе (европейский фахверк), в странах Восточной и Юго-Восточной Азии, Африки, Америки, Океании. Дерево - материал, созданный для человеческого жилья самой природой Жить в таком доме не только комфортно, но и престижно, он указывает на соответствующий социальный статус семьи. В экономически развитых странах из дерева возводят семейные дома, что и определило выбор данной темы и ее актуальность.

Список литературы

1.         СНиП II-25-80. Нормы проектирования. Деревянные конструкции. – М.: Стройиздат, 1983. – 32 с.

2.         СНиП II-23-81*. Нормы проектирования. Стальные конструкции. – М.: ЦИТП Госстроя СССР, 1990. – 96 с.

3.         СНиП 2.03.01-84*. Нормы проектирования. Бетонные и железобетонные конструкции. / Минстрой России – М.: ГП ЦПП, 1996. – 76 с.

4.         СНиП 2.01.07-85*. Нагрузки и воздействия. / Минстрой России – М.: ГП ЦПП, 1996. – 44 с.

5.         СНиП II-3-79*. Строительная теплотехника. – М.: ГП ЦПП, 1995. – 29 с.