Расчет ППФ и его АЧХ

2.8 Расчет ППФ и его АЧХ

Фильтры СВЧ применяют для частотной селекции сигналов, согласования комплексных нагрузок, в цепях задержки и в качестве замедляющих систем.

Фильтры являются обычно пассивными взаимными устройствами и характеризуются частотной зависимостью вносимого в тракт затухания. Полоса частот с малым затуханием называется полосой пропускания, а полоса частот с большим затуханием – полосой заграждения. По взаимному расположению полосы пропускания и заграждения принято выделять следующие типы фильтров: фильтр нижних частот (ФНЧ), пропускающие сигналы ниже заданной граничной частоты и подавляющие сигналы с частотами выше граничной; фильтры верхних частот (ФВЧ), пропускающие сигналы на частотах выше заданной и подавляющие сигналы других частот; полосно-пропускающие (полосовые) фильтры (ППФ), пропускающие сигналы в пределах заданной полосы частот и подавляющие сигналы вне этой полосы, полосно-заграждающие (режекторные) фильтры (ПЗФ), подавляющие сигналы в пределах заданной полосы частот и пропускающие сигналы вне этой полосы.

Частотная характеристика каждого фильтра имеет переходную область между полосой пропускания и полосой заграждения, то есть между частотами и . В этой области затухание меняется от максимального значения до минимального. Обычно стараются уменьшить эту область, что приводит к усложнению фильтра, увеличению числа его звеньев. При проектировании фильтров, как правило, задаются следующие характеристики: полоса пропускания, полоса заграждения, средняя частота, затухание в полосе пропускания, затухание в полосе заграждения, крутизна изменения затухания в переходной области, уровень согласования по входу и по выходу, характеристики линии передачи, в которую включается фильтр, тип линии передачи. Иногда оговариваются фазовые характеристики фильтра [6].

В данной курсовой работе необходимо рассчитать ППФ, используя следующие данные: МГц, дБ, МГц, дБ.

2.8.1 Расчет низкочастотного фильтра прототипа

В настоящее время наиболее распространенной методикой расчета фильтров СВЧ является методика, согласно которой вначале рассчитывается низкочастотный фильтр-прототип. Нахождение параметров схемы фильтра-прототипа по заданной частотной характеристике фильтра является задачей параметрического синтеза. Для общности результатов все величины нормируются. Сопротивления нагрузки и генератора принимаются равными единице. Наряду с нормировкой по сопротивлению проводится нормировка по частоте, например граничная частота полосы пропускания фильтра принимается равной единице. Таким образом, расчет фильтра СВЧ сводится к синтезу схемы низкочастотного прототипа и замене элементов с сосредоточенными параметрами их эквивалентами с распределенными параметрами.

Для аппроксимации частотных характеристик применяется ряд функций, удовлетворяющих условиям физической реализуемости фильтров. Наиболее распространенными являются максимально плоская и равноволновая аппроксимации, использующие полиномы Баттерворта и Чебышева соответственно.

Рассчитаем фильтр с максимально плоской характеристикой затухания. Она монотонно возрастает при повышении частоты:

,

где - число звеньев фильтра прототипа;

 - нормированная частота;

 - коэффициент пульсаций;

 - граничная частота полосы пропускания;

 - затухание на частоте

Максимально плоская характеристика затухания фильтра – прототипа нижних частот представлена на рисунке 2.16

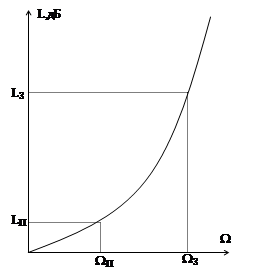Рисунок 2.16 - Максимально плоская характеристика затухания фильтра – прототипа нижних частот

Число звеньев фильтра прототипа  может быть найдено из требований к АЧХ фильтра. Так, для фильтра с максимально плоской АЧХ число звеньев определяется следующим образом:

,

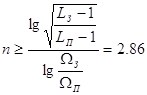Возьмем , тогда схема фильтра-прототипа нижних частот будет выглядеть следующим образом

Схема фильтра-прототипа нижних частот представлена на рисунке 2.17

Рисунок 2.18 - Схема фильтра-прототипа нижних частот

Параметры фильтра с максимально плоской характеристикой можно рассчитать по следующей формуле:

,

где   - коэффициент пульсаций;

Таким образом,

g₀=1, g₁=0.914, g₂=1.829, g₃=0.914, g₄=1.

Денормировки параметров фильтра производится с помощью соотношений:

,  ,

Здесь обозначения со штрихами относятся к нормированным параметрам фильтра-прототипа, без штрихов - к денормированным: , , , , .

Так как будущий фильтр будем ставить в коаксиальный тракт передачи, то Ом, тогда