Навигация
Наклон каждой асимптоты кратен 20 дБ /дек
2. Наклон каждой асимптоты кратен 20 дБ /дек.
По ЛАЧХ можно восстановить частотную передаточную функцию.
Передаточные функции следящих систем
Из изложенного выше следует, что любая из передаточных функций: операторный коэффициент передачи W(p), передаточная функция W(s) и частотная передаточная функция (комплексный коэффициент передачи) W(jw) может быть получена путем замены переменных в известном выражении для одной из вышеназванных передаточных функций.
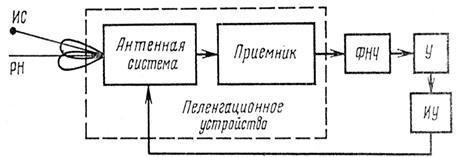
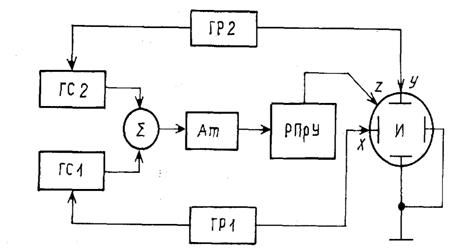
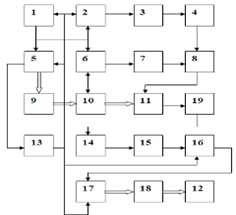
Определим передаточные функции, связывающие входные и выходные переменные в замкнутой следящей системе, представленной математической моделью (рис. 2).
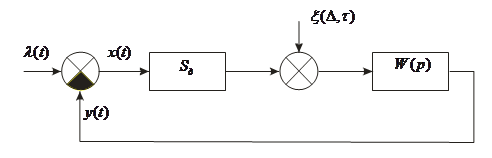
Рис. 2. Структурная схема следящей системы
Исходные соотношения:
![]() – ошибка слежения. (1)
– ошибка слежения. (1)
В свою очередь
![]() (2)
(2)
Подставим (1) в (2) и сгруппируем слагаемые. В результате получим
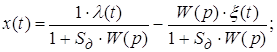
![]() ,
,
где 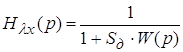 и
и 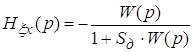 ─ соответственно передаточные функции от воздействия к ошибке и от возмущения к ошибке.
─ соответственно передаточные функции от воздействия к ошибке и от возмущения к ошибке.
Найдены, таким образом, передаточные функции, связывающие ошибку слежения с входным воздействием и с флюктуационной составляющей.
Теперь подставим (1) в (2) и сгруппируем слагаемые
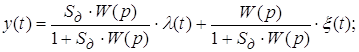
![]()
где 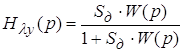 и
и 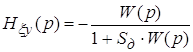 .
.
![]() и
и ![]() – передаточные функции от воздействия к управляемой величине (связывающие входную и выходную величины) и от возмущения к управляемой величине.
– передаточные функции от воздействия к управляемой величине (связывающие входную и выходную величины) и от возмущения к управляемой величине.
Можно значительно упростить процесс определения передаточной функции, если использовать следующую формулу:
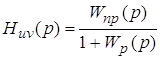 ,
,
где u – входное воздействие, а v – выходная величина;
![]() – передаточная функция прямой цепи, связывающей входное воздействие и выходную величину.
– передаточная функция прямой цепи, связывающей входное воздействие и выходную величину.
![]() – передаточная функция разомкнутой системы (размыкается в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) .
– передаточная функция разомкнутой системы (размыкается в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) .
Передаточные функции в обобщенной структурной схеме радиотехнической следящей системы
Основная передаточная функция – передаточная функция замкнутой системы. Определяется отношением изображений по Лапласу управляемой величины и задающего воздействия:
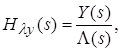
где ![]()
![]()
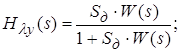
Передаточная функция разомкнутой системы – отношение изображений по Лапласу управляемой величины и ошибки слежения.
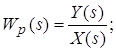
![]()
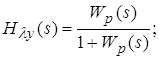
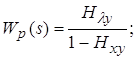
Передаточная функция от воздействия к ошибке – отношение изображений ошибки и задающего воздействия:
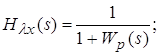
![]() – передаточная функция от возмущения к управляемой величине:
– передаточная функция от возмущения к управляемой величине:
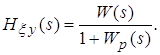
Типовые динамические звенья следящих систем
Для упрощения анализа следящих систем сложные динамические звенья, описываемые дифференциальным уравнениями высоких порядков, разбивают на ряд простых таким образом, чтобы дифференциальные уравнения, описывающие их работу, были не выше второго порядка:
![]() .
.
Этому уравнению соответствует передаточная функция
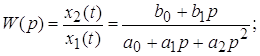
Всё множество динамических звеньев, независимо от назначения, конструктивных особенностей, элементной базы классифицируется по виду дифференциального уравнения, описывающего работу звена или его передаточной функции. По этому признаку классификации различают следующие типы динамических звеньев:
- позиционные;
- интегрирующие;
- дифференцирующие.
К позиционным звеньям относятся: безынерционное, апериодическое звено 1-ого порядка, апериодическое звено 2-ого порядка, колебательное звено.
К дифференцирующим звеньям относятся: идеальное дифференцирующее, инерционное дифференцирующее, форсирующее.
К интегрирующим звеньям относятся: идеальное интегрирующее, инерционное интегрирующее, изодромное.
Апериодическое звено 1ого порядка описывается ДУ следующего вида:
![]() или
или ![]()
где ![]() – выходная величина;
– выходная величина; ![]() (t) – входная величина; Т─ постоянная времени звена; k─ коэффициент передачи.
(t) – входная величина; Т─ постоянная времени звена; k─ коэффициент передачи.
Передаточная функция
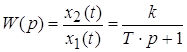 ;
;
![]() ,
,
где ![]() ;
; ![]() .
.
К этим звеньям относятся исполнительные двигатели, усилители мощности, магнитные усилители , RC – фильтры.
АЧХ звена определяется выражением:
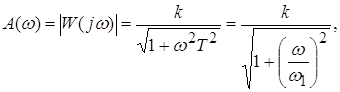
где ![]() – сопрягающая частота.
– сопрягающая частота.
ФЧХ звена: ![]()
Переходная характеристика:
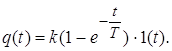
Весовая функция
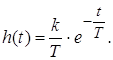
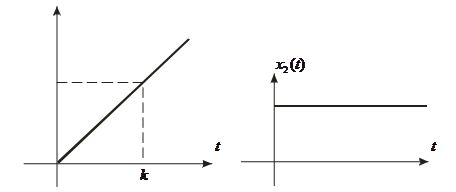
Графическое изображение переходной и весовой функции (рис. 3):
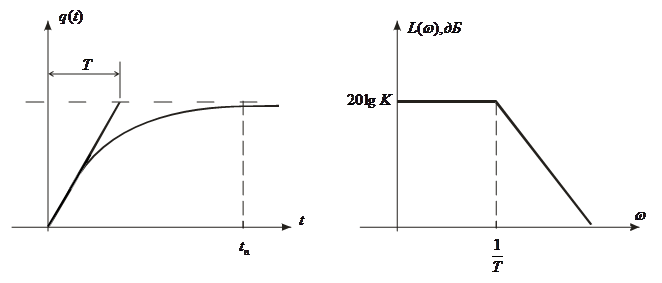
Рис. 3. Переходная и весовая характеристики апериодического звена
Логарифмическая амплитудно-частотная характеристика
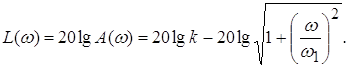
Длительность переходного процесса tп = 3T; q(tп) = 0,95q.
Полоса пропускания ![]()
При уменьшении постоянной времени Т увеличивается ωп, и при Т = 0 переходная характеристика будет повторять входной процесс, и в результате получим звено, описываемое уравнением
![]() ;
;
такое звено называется безынерционным ![]() ;
;
Передаточная функция, АЧХ и ФЧХ звена соответственно равны:
W(s) = k; A(ω) = k;Ψ(ω) = 0.
К безынерционным звеньям обычно относят звенья, ширина спектра сигналов, на входах которых значительно уже полосы пропускания.
Рассмотрим пример RC – цепи (рис.4)
Такая цепь относится к апериодическому звену и имеет передаточную функцию
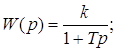
где T =R1R2C/R1+R2.
![]()
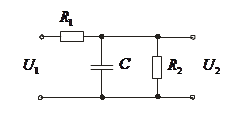
Рис.4. Пример апериодического звена
При ![]() и апериодическое звено трансформируется в безынерционное звено.
и апериодическое звено трансформируется в безынерционное звено.
ЛИТЕРАТУРА
1. Коновалов. Г.Ф. Радиоавтоматика: Учебник для вузов. – М.: Высш.шк., 2000.
2. Радиоавтоматика: Учеб. пособие для вузов./ Под ред. В.А. Бесекерского.- М.: Высш. шк., 2005.
3.. Первачев. С.В Радиоавтоматика: Учебник для вузов.- М.: Радио и связь, 2002.
4. Цифровые системы фазовой синхронизации/ Под ред. М.И. Жодзишского – М.: Радио, 2000
Похожие работы
... дифференцирующего звена Форсирующее звено представляет собой параллельное соединение безынерционного и идеального дифференцирующего звеньев: . Звено используется для коррекции передаточных функций систем (компенсирует запаздывание фазы, вносимое интегрирующими звеньями). Характеристики звена (рис.7): ; ; . Рис. 8. Характеристики форсирующего звена Интегрирующие звенья. К идеальным ...
... следит система. Целью проектирования является расчет основных параметров системы, удовлетворяющих системе заданных показателей качества. Исходные данные Система автосопровождения источника сигнала по направлению (АСН). Порядок астатизма системы – первый. Постоянная времени простого инерционного звена: T = 0,5 с. Максимальная скорость воздействия: a1 = 10 º/с. Максимальное ускорение ...
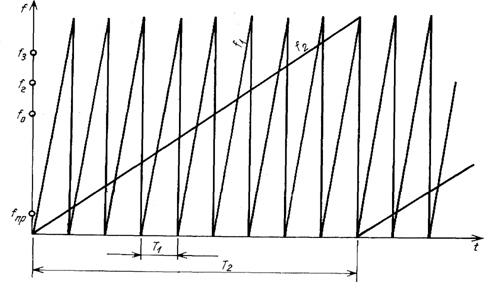
... 2. Разработка структурной схемы устройства 2.1 Расчёт основных системных показателей В данном разделе даётся описание метода обобщенной (однокритериальной) оценки частотной избирательности радиоприёмника, а так же соображения о построении аппаратуры. Предполагается применение двухчастотного зондирования с имитацией статистических характеристик прогнозируемой электромагнитной обстановки. ...
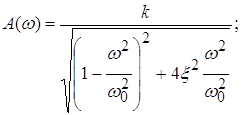
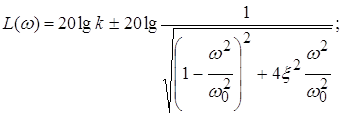

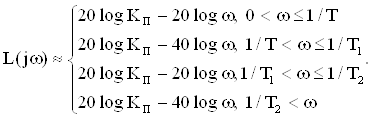
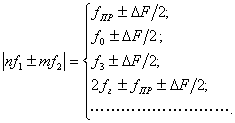
0 комментариев