Навигация
Колебания маятника с различными механизмами затухания
17191
знак
0
таблиц
3
изображения
Введение
Сейчас уже невозможно проверить легенду о том, как Галилей, стоя на молитве в соборе, внимательно наблюдал за качением бронзовых люстр. Наблюдал и определял время, затраченное люстрой на движение туда и обратно. Это время потом назвали периодом колебаний. Часов у Галилея не было, и, чтобы сравнить период колебаний люстр, подвешенных на цепях разной длины, он использовал частоту биения своего пульса.
Маятники используют для регулировки хода часов, поскольку любой маятник имеет вполне определенный период колебаний. Маятник находит также важное применение в геологической разведке. Известно, что в разных местах земного шара значения g различны. Различны они потому, что Земля - не вполне правильный шар. Кроме того, в тех местах, где залегают плотные породы, например некоторые металлические руды, значение g аномально высоко. Точные измерения g с помощью математического маятника иногда позволяют обнаружить такие месторождения.
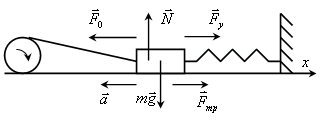
Целью данной курсовой работы является изучение колебаний маятника с различными механизмами затухания на примерах физического и пружинного маятников, где физический маятник - тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела, а пружинный маятник может быть осуществлен в виде груза массой m и невесомой пружины жесткостью k.
Реализовать поставленную цель можно решив ряд задач:
- определение исходных теоретических положений;
- изучение и анализ литературы, посвященной данным проблемам;
Объектом данной курсовой работы является маятник. Предметом – колебания маятника с различными механизмами затухания.
Для решения постановленных задач использовались научные труды следующих авторов: Андронова А.А., Витта А.А., Хайкина С.Э., Анищенко В.С., Боголюбова Н.Н., Митропольского Ю.А., Владимирова С.Н., Майдановского А.С., Новикова С.С., Горелика Г.С., Дмитриева А.С., Кислова В.Я., Капранова М.В., Кулешева В.Н., Уткина Г.М., Ланда П.С., Мигулина В.В., Медведева В.И., Неймарка Ю.И., Рабиновича М.И., Трубецкова Д.И. и некоторых других.
1. Уравнения собственных затухающих колебаний маятника
1.1 Общие характеристики колебаний
Колебаниями называются процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качания маятника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата центра масс, в случае переменного тока колеблются напряжение и сила тока. Физическая природа колебаний может быть разной, однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями.[1] Далее рассмотрим затухающие колебания.
Затухающими колебаниями называют собственные колебания, амплитуда А которых убывает со временем t по закону экспоненты А(t)=Аоexp (-?t) (? - показатель затухания из-за диссипации энергии благодаря силам вязкого трения для механических затухающих колебаний и омическому сопротивлению для электромагнитных затухающих колебаний). Количественно затухающие колебания характеризуются декрементом затухания ?, добротностью Q = ?/? и временем затухания ? = 1/?, за которое амплитуда затухающих колебаний убывает в e = 2,73 раза.[2]
Затухание колебаний, уменьшение интенсивности колебаний с течением времени, обусловлено потерей энергии колебательной системой. Простейшим случаем уменьшения энергии колебания является превращение ее в тепло вследствие трения в механических системах и сопротивления в электрических системах. В последних, затухание колебаний происходит также вследствие излучения электромагнитной энергии. Закон затухания колебаний определяется характером потерь энергии и другими свойствами системы. Наиболее изученным является случай, когда затухание колебаний обусловлено уменьшением энергии, пропорциональным квадрату скорости движения в механической системе или соответственно квадрату силы тока в электрической системе, это справедливо для линейных систем. В этом случае затухание колебаний имеет экспоненциальный характер, т.е. размахи колебаний убывают по закону геометрической прогрессии.
Потери энергии в системе, вызывая затухание колебаний, нарушают их периодичность, поэтому затухающие колебания не являются периодическим процессом и, строго говоря, к ним неприменимо понятие периода или частоты. Однако, когда затухание мало, состояния в системе приблизительно повторяются и можно условно пользоваться понятием периода как промежутка времени между двумя последующими прохождениями колеблющейся физической величины (тока, напряжения, размаха колебаний маятника и т.д.) в одну и ту же сторону через максимальное значение. Оценку относительного уменьшения амплитуды колебаний за период дает логарифмический декремент затухания. Скорость затухание колебаний связана с добротностью колебательной системы.
Декремент затухания – количественная характеристика быстроты затухания колебаний. Декремент затухания d равен натуральному логарифму отношения двух последующих максимальных отклонений х колеблющейся величины в одну и ту же сторону: .
Декремент затухания – величина, обратная числу колебаний, по истечении которых амплитуда убывает в е раз. Например, если d=0,01, то амплитуда уменьшится в е раз после 100 колебаний. Декремент затухания характеризует число периодов, в течение которых происходит затухание колебаний, а не время такого затухания. Полное время затухания определяется отношением Т/d.[3]
Добротность колебательной системы, отношение энергии, запасенной в колебательной системе, к энергии, теряемой системой за один период колебания. Добротность характеризует качество колебательной системы, т.к. чем больше Добротность колебательной системы, тем меньше потери энергии в системе за одно колебание. Добротность колебательной системы Q связана с логарифмическим декрементом затухания d. При малых декрементах затухания Q»p/d. В колебательном контуре с индуктивностью L, емкостью C и омическим сопротивлением R добротность колебательной системы
где w - собственная частота контура. В механической системе с массой m, жесткостью k и коэффициентом трения b.
Добротность колебательной системы
Добротность - количественная характеристика резонансных свойств колебательной системы, указывающая, во сколько раз амплитуда установившихся вынужденных колебаний при резонансе превышает амплитуду вынужденных колебаний вдали от резонанса, т. е. в области столь низких частот, где амплитуду вынужденных колебаний можно считать не зависящей от частоты. На этом свойстве основан метод измерения Добротность колебательной системы величина добротности характеризует также и избирательность колебательной системы. Чем больше добротность, тем уже полоса частот внешней силы, которая может вызвать интенсивные колебания системы.
Экспериментально добротность колебательной системы обычно находят как отношение частоты собственных колебаний к полосе пропускания системы, т.е. Q=w/Dw.
Численные значения добротности колебательной системы:
- для радиочастотного колебательного контура 30 - 100;
- для камертона 10000;
- для пластинки пьезокварца 100000;
- для объемного резонатора СВЧ колебаний 100 - 100000.[4]
Похожие работы
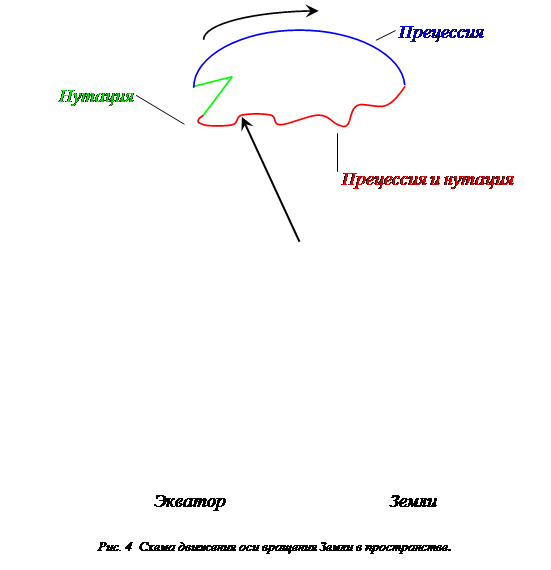
... более прозаично связаны с периодическими колебаниями физических систем и воздействием на них сторонних сил, имеющих также физическую природу. Итак, природные катаклизмы вызываются периодическими колебаниями системы атмосфера – океан – Земля под воздействием Солнца (прецессия), неравномерности прогрева атмосферы (воздействие воздушных масс на Землю), неравномерным прогревом океана (океанические ...
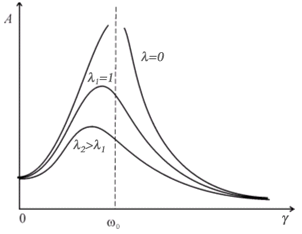
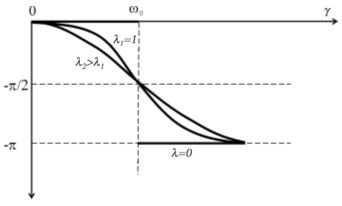
... частоты вынуждающей силы) характеристики. Графически эти зависимости при различных значениях приведены на рисунках 5 и 6: Рис.5 Амплитудно-частотные характеристики Рис.6 Фазово-частотные характеристики Отметим здесь, что в отсутствие трения изменение фазы вынужденных колебаний на величину происходит скачком при . Учет трения размазывает этот скачок. При установившемся ...
... , нужно посредством правил подсчета значащих цифр округлить результат математических вычислений так, чтобы точность их соответствовала точности данных, полученных от измерения. ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА Цель работы Экспериментальная проверка основных уравнений и законов поступательного движения тела на специально сконструированной для этого ...
... геномах растений, вызываемые с помощью ФПУ-трансформированной человеческой речи, которая резонансно взаимодействует с хромосомной ДНК in vivo [25,29]. Этот результат, осмысленный нами с позиций семиотико-волновой составляющей генетического кода, имеет существенное методологическое значение и для анализа таких суперзнаковых объектов, как тексты ДНК, и для генома в целом. Открываются принципиально ...
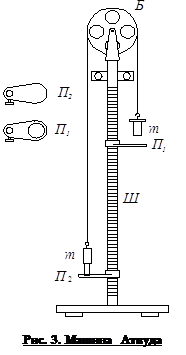
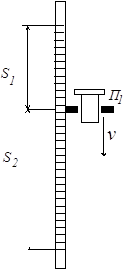
0 комментариев