Навигация
Уравнение собственных затухающих колебаний физического и пружинного маятников
1.2 Уравнение собственных затухающих колебаний физического и пружинного маятников
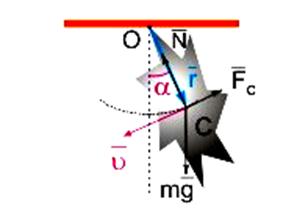
Рассмотрим движение груза, жестко зафиксированного на подвесе (металлическом стержне), закрепленном в точке O (см. приложение 1). Система «груз – подвес» в общем случае представляет собой физический маятник. Точку крепления этого маятника условно назовем точкой подвеса.
Опыт показывает, что физический маятник, выведенный из положения равновесия, совершает вращательные колебания. Согласно основному закону динамики вращательного движения произведение момента инерции системы «груз – подвес» на угловое ускорение маятника равно равнодействующему моменту внешних сил: силы тяжести m·g и силы сопротивления Fc (момент силы деформации растяжения тела N равен нулю). Спроецировав это уравнение на направление оси вращения, для случая малых колебаний получим следующее выражение:
I·a" = M + Mc = - k·a - h·a', (1)
где α(t) - угол отклонения колеблющегося груза, отсчитываемый от положения равновесия;
α' и α" - соответственно угловая скорость и угловое ускорение маятника;
k и h - размерные константы;
I - момент инерции системы «груз – подвес»;
М = -m.g.r.sin(α) = -k.sin(α) - момент возвращающей силы (для малых колебаний М = -k.α);
Mc = -h.α' - момент сил сопротивления (выражение справедливо для малых угловых скоростей).[5]
Поделив левую и правую части уравнения (1) на величину I и перенеся все слагаемые в левую часть, получим соотношение, аналогичное выражению, описывающему движение собственных затухающих колебаний груза на пружине.
a" + w02·a + 2b·a' = 0, (2)
где b = h/2I - коэффициент затухания;
w0 = (k/I)1/2 - собственная частота колебаний груза.
Решение уравнения (2) имеет вид:
a(t) = a0·e-bt·sin(w·t + j), (3)
где w=(w02 - b2)1/2 - частота затухающих колебаний груза.
Как видно из уравнения (3) амплитуда углового смещения будет уменьшаться (затухать) с течением времени по экспоненциальному закону. Коэффициент затухания определяет быстроту этого процесса. Он равен промежутку времени по истечении которого, амплитуда колебаний уменьшается в e раз.
Далее рассмотрим уравнение собственных затухающих колебаний пружинного маятника.
Пружинным маятником называется система, состоящая из груза массой m и невесомой пружины жесткостью k.
Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как рассматриваем только линейные системы, b = const, k = const. x - смещение маятника от положения равновесия.
![]()
(второй закон Ньютона)
Данное уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Принято записывать его в следующем, так называемом каноническом виде:
![]()
![]()
![]()
- коэффициент затухания, - собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто w.
Уравнение затухающих колебаний в таком (каноническом) виде описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для b и j0.
2. Движения маятника с различными механизмами затухания
При исследовании собственных колебаний предполагается отсутствие внешней среды. Наличие среды приводит к появлению диссипативной силы, которая, как мы показали, постепенно уменьшает первоначально переданную системе энергию. Это выражается через уменьшение собственной частоты колебаний ω0, также как постепенным уменьшением амплитуды колебаний.
Примечание: во избежание путаницы нумерация формул останется такой же как в научной литературе.[6]
Пусть на колеблющееся тело действует сила мокрого трения:
![]()
![]()
![]()
![]() ,
,
Уравнение движения частицы примет следующий вид:
![]()
![]()
![]()
![]() , (1.35)
, (1.35)
где
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . (1.36)
. (1.36)
Подставляя последнее в (1.35), получим:
![]()
![]()
![]()
![]() (1.37).
(1.37).
Так как полученное уравнение верно для произвольного момента времени, то выражение в скобках должно быть нулем. Последнее дает для неизвестной величины ![]()
![]()
![]()
![]()
![]() следующее значение
следующее значение
![]()
![]()
![]()
![]() (1.38)
(1.38)
где
![]() , (1.39)
, (1.39)
Учитывая (1.38), решение (1.36) примет следующий вид:
![]()
![]()
![]()
![]() , (1.40)
, (1.40)
Полученное уравнение движения описывает затухающие колебания, где![]()
![]()
![]()
![]()
![]() и
и ![]()
![]()
![]()
![]() – постоянные, определяемые из начальных условий.
– постоянные, определяемые из начальных условий.
В зависимости от соотношения коэффициента трения ![]()
![]()
![]()
![]() и частоты собственных колебаний
и частоты собственных колебаний ![]()
![]()
![]()
![]() , затухающие колебания подразделяются на два класса. Они соответствуют случаям периодического и непериодического затухания.
, затухающие колебания подразделяются на два класса. Они соответствуют случаям периодического и непериодического затухания.
Периодическое затухание. Оно осуществляется при слабых силах трения:
![]() , (1.41)
, (1.41)
когда величина (1.39) действительна. В этом случае решение (1.40) выражается формулой (в действительной форме)
![]()
![]()
![]()
![]() , (1.42)
, (1.42)
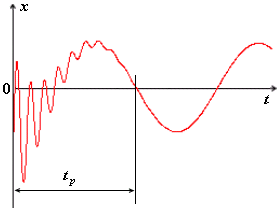
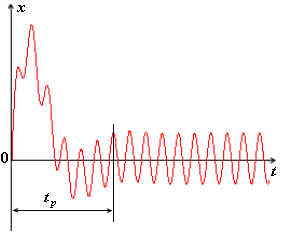
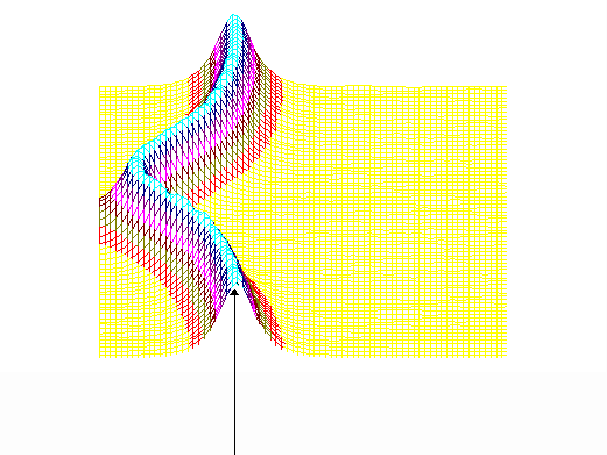
Графически это колебание представлено на рисунке (см. приложение 2) и является колебанием с постоянной частотой (1.39), но убывающей с течением времени амплитудой. В этом смысле это не только не гармоническое, но даже и не периодическое колебание, поскольку колебания не повторяются в том же виде. Тем не менее, удобно говорить о периоде этих колебаний, понимая под этим промежуток времени
![]() , (1.43)
, (1.43)
Говоря «амплитуда затухающих колебаний» понимают величину
![]() , (1.44)
, (1.44)
![]() которая есть максимальное смещение частицы относительно положения равновесия во время колебаний. Из выражения (1.44) следует, что за время
которая есть максимальное смещение частицы относительно положения равновесия во время колебаний. Из выражения (1.44) следует, что за время ![]() , (1.45) амплитуда убывает в
, (1.45) амплитуда убывает в ![]()
![]()
![]()
![]() раз. Этот промежуток времени называется временем затухания, а
раз. Этот промежуток времени называется временем затухания, а ![]() – декрементом затухания.
– декрементом затухания.
Наиболее объективной характеристикой затухания колебаний является логарифмический декремент, который является отношением периода колебаний (1.43) к времени затухания (1.45)
![]()
![]() , (1.46)
, (1.46)
Легко заметить, что логарифмический декремент равен натуральному логарифму отношения двух последующих амплитуд:
![]()
![]()
![]()
![]() , (1.47)
, (1.47)
Определим число N колебаний, в течение которых амплитуда колебаний убывает в ![]()
![]()
![]()
![]() , раз:
, раз:
![]()
![]()
![]()
![]()
откуда следует, что
![]()
![]()
![]()
![]() , (1.48)
, (1.48)
На основании этого соотношения можно экспериментально определить логарифмический декремент затухания ![]()
![]()
![]()
![]() , считая соответствующее число
, считая соответствующее число ![]()
![]()
![]()
![]() колебаний.
колебаний.
Непериодическое затухание. При сильном трении
![]()
![]()
![]()
![]() (1.49)
(1.49)
величина (1.43) становится мнимой. В этом случае удобно представить (1.42) так:
![]() , (1.50)
, (1.50)
![]()
![]() , (1.51)
, (1.51)
В рассматриваемом случае решение (1.42) примет вид:
![]()
![]()
![]()
![]() , (1.52)
, (1.52)
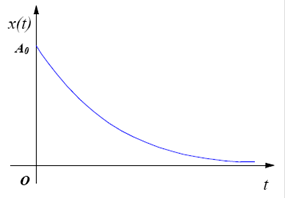
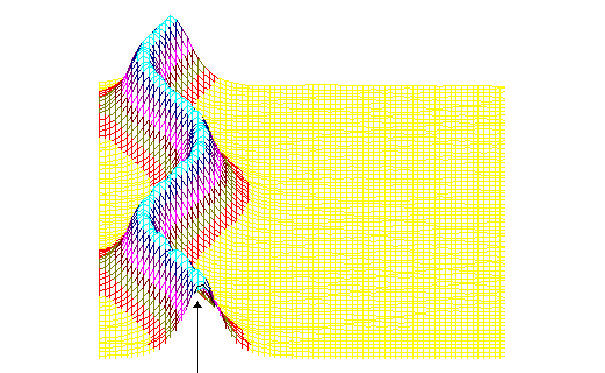
которое не описывает какое-либо колебание, а представляет экспоненциональное убывание смещения от положения равновесия (см. приложение 3). Непериодическое затухание маятника можно наблюдать, если поместить его в сильно вязкую среду (глицерин, мед).
![]() Специальным случаем непериодического затухания является случай, когда
Специальным случаем непериодического затухания является случай, когда ![]()
![]()
![]() . В этом случае решение уравнения (1.35) выражается в виде:
. В этом случае решение уравнения (1.35) выражается в виде:
![]() , (1.53).
, (1.53).
Заключение
Целью данной курсовой работы являлось изучение колебаний маятника с различными механизмами затухания. Для реализации поставленной цели предполагалось решение ряда задач, что позволило сделать следующие выводы:
На основании анализа существующей литературы даны определения исходных теоретических положений, а именно: колебания, виды колебаний, маятник (физический маятник, пружинный маятник), декремент затухания, добротность колебательной системы и т.д.
Также, исходя из проработанной литературы, сделан вывод о том, что данная тема изучалась и изучается многими авторами, как зарубежными, так и советскими, и находит практическая применение в различных науках.
Получены уравнения собственных затухающих колебаний на примерах физического и пружинного маятников.
![]() ,
,
![]()
![]() где - коэффициент затухания,
где - коэффициент затухания,
- собственная частота свободных (незатухающих) колебаний пружинного маятника.
Таково полученное уравнение собственных затухающих колебаний пружинного маятника. Это уравнение описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для b и j0.
a(t) = a0·e-bt·sin(w·t + j), (3)
где w=(w02 - b2)1/2 - частота затухающих колебаний груза.
Данное уравнение определяет быстроту процесса затухания колебаний физического маятника.
Определены два механизма затухающих колебаний: периодическое (осуществляется при слабых силах трения) и непериодическое (при сильном трении), а также получены формулы, для их расчета.
![]() - для периодического механизма затухающих колебаний;
- для периодического механизма затухающих колебаний;
![]() ,
, ![]() - для непериодического механизма затухающих колебаний.
- для непериодического механизма затухающих колебаний.
Список сокращений
г. – год;
пр. – прочее;
с. – страница;
см. – смотреть;
т.д. – так далее;
т.е. – то есть;
Библиографический список литературы
1. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Наука, 1991. - 568 с.
2. Анищенко В.С. Сложные колебания в простых системах. М.: Наука, 1990. – 59 с.
3. Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1994. - 408 с.
4. Владимиров С.Н., Майдановский А.С., Новиков С.С. Нелинейные колебания многочастотных автоколебательных систем. Томск: изд-во Томск. ун-та, 1993. - 203 с.
5. Горелик Г. С., Колебания и волны, 2 изд., М., 1989. - 124 с.
6. Дмитриев А.С., Кислов В.Я. Стохастические колебания в радиофизике и электронике. М.: Наука, 2001. - 280 с.
7. Капранов М.В., Кулешев В.Н., Уткин Г.М. Теория колебаний в радиотехнике. М.: Наука, 1994. - 319 с.
8. Ланда П.С. Автоколебания в системах с конечным числом степеней свободы. М.: Наука, 1991. - 360 с.
9. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука, 1989. - 390 с.
10. Мун Ф. Хаотические колебания: Вводный курс для научных работников и инженеров. М.: Мир, 1990. - 312 с.
11. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания. М.: Наука, 1995. - 424 с.
12. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука, 1994. - 431 с.
13. Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 2002. - с. 597.
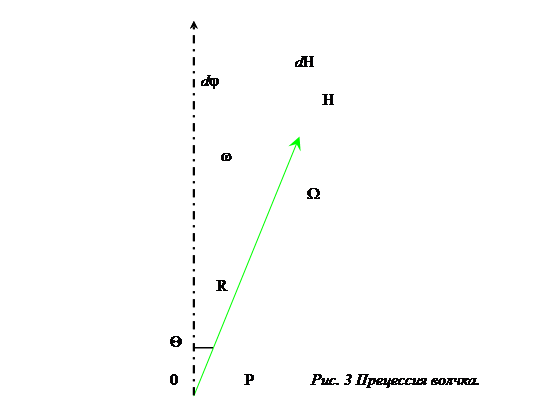
Приложение 1
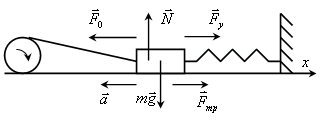
Приложение 2

Приложение 3
[1] Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Наука, 1991. - с. 137.
[2] Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука, 1989. - с. 52.
[3] Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 2002. - с. 597.
[4] Горелик Г.С., Колебания и волны, 2 изд., М., 1989. – с. 82
[5] Мун Ф. Хаотические колебания: Вводный курс для научных работников и инженеров. М.: Мир, 1990. - с. 192.
[6] Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 2002. - с. 149-154.
Похожие работы
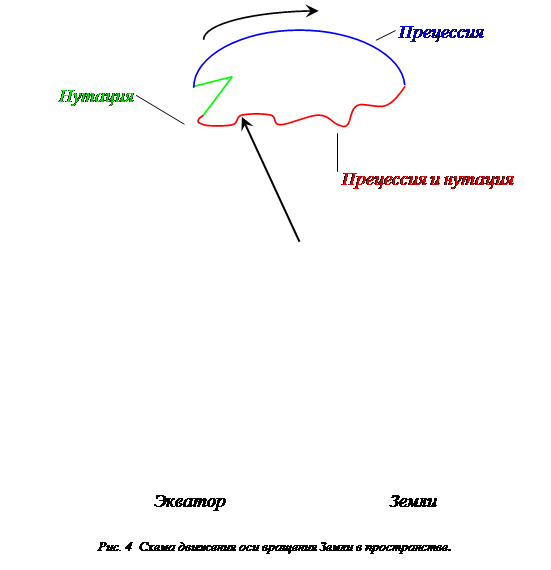
... более прозаично связаны с периодическими колебаниями физических систем и воздействием на них сторонних сил, имеющих также физическую природу. Итак, природные катаклизмы вызываются периодическими колебаниями системы атмосфера – океан – Земля под воздействием Солнца (прецессия), неравномерности прогрева атмосферы (воздействие воздушных масс на Землю), неравномерным прогревом океана (океанические ...
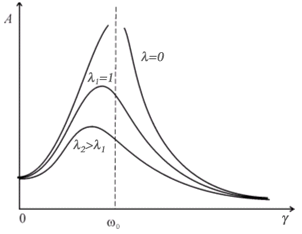
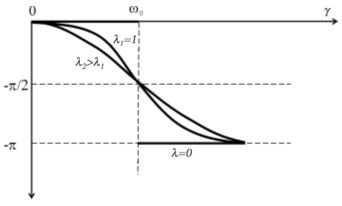
... частоты вынуждающей силы) характеристики. Графически эти зависимости при различных значениях приведены на рисунках 5 и 6: Рис.5 Амплитудно-частотные характеристики Рис.6 Фазово-частотные характеристики Отметим здесь, что в отсутствие трения изменение фазы вынужденных колебаний на величину происходит скачком при . Учет трения размазывает этот скачок. При установившемся ...
... , нужно посредством правил подсчета значащих цифр округлить результат математических вычислений так, чтобы точность их соответствовала точности данных, полученных от измерения. ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА Цель работы Экспериментальная проверка основных уравнений и законов поступательного движения тела на специально сконструированной для этого ...
... геномах растений, вызываемые с помощью ФПУ-трансформированной человеческой речи, которая резонансно взаимодействует с хромосомной ДНК in vivo [25,29]. Этот результат, осмысленный нами с позиций семиотико-волновой составляющей генетического кода, имеет существенное методологическое значение и для анализа таких суперзнаковых объектов, как тексты ДНК, и для генома в целом. Открываются принципиально ...



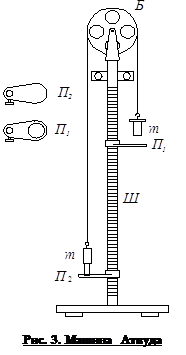

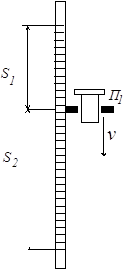
0 комментариев