В каждый такой массив попадают микросостояния одного уровня

17. В каждый такой массив попадают микросостояния одного уровня.

Общий уровень называется терм. Каждая терм характеризуется двумя суммарными квантовыми числами L и S. Кратность вы­рождения терма определяется числом принадлежащих ему микросостояний и равна произ­ведению (2L+1)´(2S+1).

Это L-S-термы или термы Рассел-Саундерса.

Номенклатура термов в первую очередь учитывает эти два признака:

во-первых, величину орбитального момента импульса.

во-вторых, величину спинового момента импульса.

По величине суммарного L термы называются:

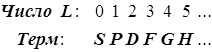
По величине суммарного спина S вводится мультиплетность, равная 2S+1, и термы

получают дополнительное наименование – символ мультиплетности:

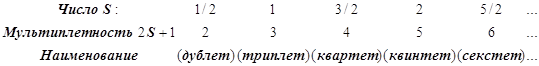
Результирующий символ атомного терма Рассел-Саундерса имеет вид  

Резюме:

По этим признакам конфигурация  порождает 15 микросостояний электронной оболочки, и они группируются в три терма:

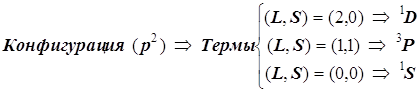
18. Следующая поправка к энергии оболочки атома имеет релятивистское происхождение и непосредственно не связана с кулоновским эффектами. Она называется спин-орбитальным эффектом. Название «спин-орбитальное взаимодействие» устоявшееся, но физически не вполне точное. Это просто привычный термин... .

Спин-орбитальный эффект приводит к тому, что термы Рассел-Саундерса расщепляются на несколько подуровней, каждый из которых характеризуется внутренним квантовым числом, принимающим значения . Внутреннее квантовое число J определяет мо­дуль суммарного момента импульса электронной оболочки, а, соответственно, суммарного магнитного момента атома.

Спин-орбитальный эффект воз­никает в том случае, когда оба из независимых моментов импульса электронной оболочки атома, орбитальный и спиновый не равны нулю. Если же хотя бы один из них равен нулю, то спин-орбитальный эффект не имеет места.

19. Низший из атомных термов на шкале энергии (основной терм) определяется комбинацией трёх пра­вил Хунда. Они следующие:

1-е правило Хунда: В пределах орбитальной конфигурации основной терм обладает

макси­мальной мультиплетностью.

2-е правило Хунда: Если в пределах орбитальной конфигурации у нескольких термов муль­типлетность одинакова, то у основного терма орбитальный момент наибольший и квантовое число L максимальное.

3-е правило Хунда: Если в пределах орбитальной конфигурации орбитальный подуро­вень заполнен менее, чем наполовину, среди термов, возникающих в результате спин-орбиталь­ного расщепления, низшему отвечает минимальное внутреннее квантовое число J (нормаль­ный терм), а при заполнении орбитального подуровня более, чем наполовину, низший терм характеризуется максимальным внутренним квантовым числом J (обращённый терм).

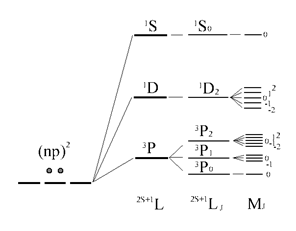
Уточняя символы атомного терма Рассел-Саундерса за счёт включения спин-орбитального эффекта, записывают их в виде . Эти термы отражают схему последовательных приближений в учёте различных сла­гаемых полной энергии коллектива электронов в атомной оболочке в отсутствие внешних силовых полей.

В итоге термы, возникающие в основной конфигурации атома углерода, представлены следующим образом:

 

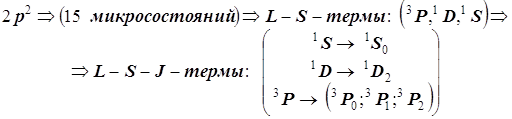
Во внешнем магнитном поле наблюдается дополнительное расщепление атомных уровней по атомному квантовому числу J. С учётом этого расщепления нумерация уровней осуществляется с помощью квантового числа M_J.

В завершение этого раздела приведём последовательность атомных уровней на каждой стадии последовательного уточнения картины взаимодействий...

Последовательность учёта электронных взаимодействий и энергетическая диаграмма атомных уровней (термов) для основной конфигурации np² атома C (или Si,...)

E

Существует очень простой приём определения основного терма атомной оболочки (мнемоническое правило Грегори).

Для этого в пределах высшего незавершённого подуровня распределяют электроны с максимально возможным спиновым распариванием. При этом по АО они распределяются таким способом, чтобы достигалось максимальное значение суммарного орбитального момента. В результате получаем микросостояние с экстремальными проекциями M _Lmax и M_Smax , значения которых совпадают с соответствующими числами L, S основного терма. ПРИМЕР 1(атом C(p²)). M _Lmax=1+0; ®L_max=2; ® D; M_Smax=1/2+1/2; ® S_max=1; ®

® 2S_max+1=3 (триплет) ; Терм ³D или точнее C (2p²) ³D

ПРИМЕР 2(атом Ti(d²)). M _Lmax=2+1; ®L_max=3; ® F; M_Smax=1/2+1/2; ® S_max=1; ®

® 2S_max+1=3 (триплет) ; Терм ³F или точнее Ti (3d²) ³F

ПРИМЕР 3(атом Fe(d⁶)). M _Lmax=2; ®L_max=2; ® D; M_Smax=5/2-1/2=2; ® S_max=2; ®

® 2S_max+1=5 (квинтет) ; Терм  ⁵D или точнее Fe (3d⁶) ⁵D

ПРИМЕР 4(атом N(p³)) . M _Lmax=0; ®L_max=0; ® S; M_Smax=3/2; ® S_max=3/2; ®

® 2S_max+1=4 (квартет) ; Терм  ⁴S или точнее N (2p³) ⁴S