Навигация
Момент импульса и его свойства
Момент импульса и его свойства
В предыдущем разделе мы уже получили многие важные соотношения, касающиеся момента импульса и его проекций. В этой главе будет доведено до конца решение задачи о квантовании момента количества движения пространственного ротатора и рассмотрены его свойства.
4.3.6.1.Согласно (4.75), не существует состояния объёмного ротатора с ![]() . Поэтому при действии на волновую функцию с максимально возможным значением
. Поэтому при действии на волновую функцию с максимально возможным значением ![]() , т.е.
, т.е. ![]() , оператор повышения
, оператор повышения ![]() становится аннигилятором – "уничтожителем"
становится аннигилятором – "уничтожителем"
![]() . (4.95)
. (4.95)
Совершенно так же оператор ![]() уничтожает состояние с
уничтожает состояние с ![]()
![]() .(4.96)
.(4.96)
4.3.6.2. Чтобы от оператора сдвига ![]() , не имеющего собственных значений, перейти к одному из операторов с конкретными собственными значениями
, не имеющего собственных значений, перейти к одному из операторов с конкретными собственными значениями ![]() и
и ![]() достаточно умножить (4.95) слева на
достаточно умножить (4.95) слева на ![]() и воспользоваться формулой (4.93):
и воспользоваться формулой (4.93):
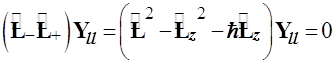 .(4.96)
.(4.96)
Отсюда на основании (4.64) и (4.91) следует
![]() , т.е.
, т.е.
![]() (4.98)
(4.98)
4.3.6.3. В силу того, что постоянная ![]() определяет квадрат модуля момента импульса, она может быть только положительной величиной, либо равной нулю
определяет квадрат модуля момента импульса, она может быть только положительной величиной, либо равной нулю![]() и, соответственно,
и, соответственно,
![]() (4.99)
(4.99)
При дискретных допустимых значениях l его минимальная величина равна нулю, а все остальные сдвигаются последовательно на единицу вверх
![]() или
или ![]() (4.100)
(4.100)
4.3.6.4. Этим охарактеризованы все свойства момента импульса при свободном вращении, а также и при вращательном движении на эквипотенциальной сферической поверхности. Квадрат модуля ![]() , сам модуль вектора
, сам модуль вектора ![]() и возможные его проекции на ось z определяются формулами
и возможные его проекции на ось z определяются формулами
![]() , где
, где ![]() , т.е.
, т.е. ![]() (4.101)
(4.101)
![]() (4.102)
(4.102)
![]() , где
, где ![]() т.е.
т.е. ![]() .(4.103)
.(4.103)
Таким образом, всякому конкретному значению модуля момента импульса ![]() отвечает
отвечает ![]() возможное значение проекции
возможное значение проекции![]() , т.е. каждому уровню вращательной энергии соответствует
, т.е. каждому уровню вращательной энергии соответствует ![]() возможных состояний пространственного ротатора. Уровень, определяемый квадратом момента импульса
возможных состояний пространственного ротатора. Уровень, определяемый квадратом момента импульса ![]() , соответственно,
, соответственно, ![]() кратно вырожден,
кратно вырожден,
4.3.6.5. В то время как проекция ![]() имеет конкретное значение, две другие проекции
имеет конкретное значение, две другие проекции ![]() и
и ![]() , как мы говорили выше, остаются неопределенными. Это имеет наглядный физический смысл, который наиболее понятен из графической иллюстрации. На рис. 4.4 представлены возможные ориентации вектора
, как мы говорили выше, остаются неопределенными. Это имеет наглядный физический смысл, который наиболее понятен из графической иллюстрации. На рис. 4.4 представлены возможные ориентации вектора ![]() при l=2 . Угол наклона вектора
при l=2 . Угол наклона вектора ![]() к оси z определяется формулой
к оси z определяется формулой
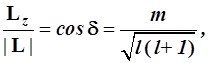 (4.104)
(4.104)
т.е, ![]() и угол
и угол ![]() никогда не равен 0. Это означает, что вектор
никогда не равен 0. Это означает, что вектор ![]() совершает прецессионное движение вокруг оси z.
совершает прецессионное движение вокруг оси z.
4.3.6.6. Обращаем еще раз внимание читателя на то, что такая ситуация порождена принципом неопределенности. Да и сама формула квантования момента импульса пространственного ротатора (4.102) в которой величина ![]() не просто пропорциональна квантовому числу l, а имеет более сложный вид, является по сути следствием этого принципа.
не просто пропорциональна квантовому числу l, а имеет более сложный вид, является по сути следствием этого принципа.
![]()
![]()
Похожие работы
т вследствие уменьшения момента инерции при сохранении момента вращения. Тут мы и убеждаемся наглядно, что чем меньше момент инерции, тем выше угловая скорость и, как следствие, короче период вращения, обратно пропорциональный ей. 3. Что такое радиоактивность (естественная и искусственная)? Как использование явлений радиоактивности позволило осуществить мечту алхимиков? Радиоактивность (от ...
... физиологическом механизме внимания также и вегетативных центров. Основные виды внимания При изучении внимания необходимо различать два основных уровня или вида его и ряд его свойств или сторон. Основными видами внимания являются непроизвольное и так называемое произвольное внимание. Непроизвольное внимание связано с рефлекторными установками. Оно устанавливается и поддерживается независимо ...
... этими двумя ветвями так велико, что его невозможно объяснить ошибками в оценке энергии Eg или потерей подпороговых g квантов, или статистическими флуктуациями. Результаты Поперечные импульсы для обоих взаимодействий (с большим и малым PT) были рассчитаны методом факториальных моментов. Из-за удобства и подобных свойств между поперечным импульсом и псевдоскоростью в вычислениях ,была ...
... полуцелые. Существуют правила отбора квантовых чисел атома: ΔL = ± 1,ΔS = 0,ΔJ = 0, ± 1 Магнитный момент атома Как уже говорилось ранее, орбитальный и магнитный моменты электрона связаны гиромагнитным отношением: . Экспериментально было доказано, что для механического и магнитного орбитальных моментов атома выполняется аналогичное соотношение . Подставляя , где L – ...


0 комментариев