Навигация
Энергетические уровни жесткого ротатора и его спектр
8308
знаков
2
таблицы
2
изображения
4.3.7. Энергетические уровни жесткого ротатора и его спектр
4.3.7.1. Поскольку квадрат момента импульса в жестком ротаторе однозначно связан с энергией (4.47), формула (4.101) позволяет легко рассчитать его уровни и спектральные термы (Т), т.е. уровни, выраженные в единицах измерения волнового числа (см–1 ) , являющегося характеристикой излучения
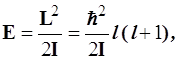(4.105)
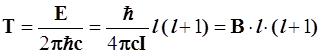.(4.105)
(4.107)
Величина В, определяемая (4.107), называется вращательной постоянной ротатора.
4.3.7.2. Обозначим величину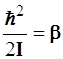 
и составим таблицу 4.5 возможных значений энергии жесткого ротатора, а на рис. 4.5. представим его энергетическую диаграмму.
4.3.7.3. Подобно плоскому ротатору, энергетическая диаграмма жесткого ротатора демонстрирует расходящуюся систему уровней, однако значительно возрастает кратность вырождения. Расстояния между соседними уровнями увеличиваются с ростом квантового числа l, причем они линейно связаны с квантовым числом нижнего уровня l:
. (4.108)
Таблица 4.5. Уровни жесткого ротатора
| l | Символ уровня | Энергия Е, | Вырождение g=2l+1 |
| 0 | S | 0 | 1 |
| 1 | P | 2 | 3 |
| 2 | D | 6 | 5 |
| 3 | F | 12 | 7 |
| 4 | G | 20 | 9 |
Рис. 4.5. Энергетическая диаграмма жесткого ротатора.
Для жесткого ротатора, например, двухатомной молекулы, разрешены спектральные переходы между соседними уровнями 
. Поэтому, согласно уравнению 4.108, ее спектр представляет собой набор линий, отстоящих друг от друга на примерно одинаковую величину, равную 
в энергетической шкале, или 2В в шкале волновых чисел 
. Поскольку вращательная постоянная связана с моментом инерции, изучение вращательных спектров молекул даёт возможность экспериментального определения момента инерции молекул и, следовательно, межатомных расстояний.
4.3.8. Волновые функции жёсткого ротатора
4.3.8.1. Использование операторов сдвигов состояний позволяет также максимально просто найти собственные функций операторов 
и 
без каких-либо специальных сведений о дифференциальных уравнениях. Авторы сознательно построили настоящий раздел в расчёте на внимательного читателя-химика, владеющего лишь минимальными, но достаточно прочными навыками в области тригонометрии и математического анализа.
4.3.8.2. Прежде всего выпишем операторы повышения и понижения в сферических координатах, используя формулы (4.53) и (4.54):
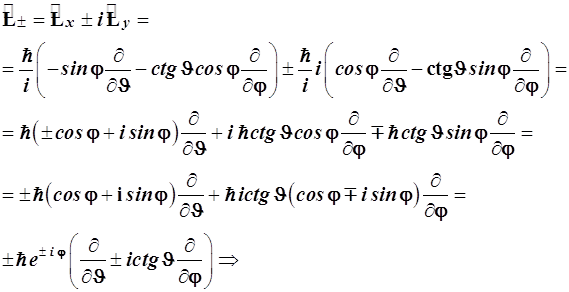
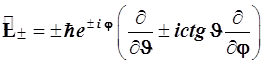(4.109)
В силу того, что собственные функции, получающиеся в результате действия операторов сдвига, подлежат нормировке, как это уже обсуждалось в разделе 4.3.5.10., мы имеем все основания определить эти операторы с точностью до постоянного множителя, т.е. вместо (4.109) ограничимся выражением
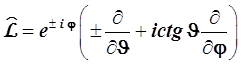(4.110)
4.3.8.3. Исходные уравнения для вывода всей цепочки волновых функций – уравнения аннигиляции
(4.111)
На основании формул (4.50) и (3.28) функцию можно 
представить в виде
(4.112)
С учётом этого уравнение (4.111) в сферических координатах: запишется в форме
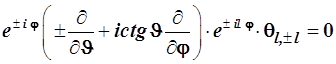.(4.113)
Совершим очень несложные преобразования, приводя к дифференциальному уравнению для функции
:
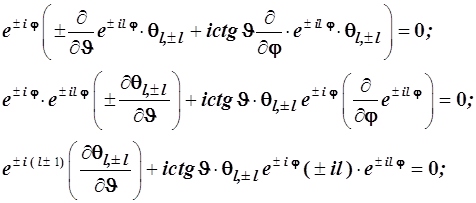
откуда следует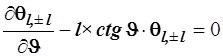 
(4.114)
Похожие работы
т вследствие уменьшения момента инерции при сохранении момента вращения. Тут мы и убеждаемся наглядно, что чем меньше момент инерции, тем выше угловая скорость и, как следствие, короче период вращения, обратно пропорциональный ей. 3. Что такое радиоактивность (естественная и искусственная)? Как использование явлений радиоактивности позволило осуществить мечту алхимиков? Радиоактивность (от ...
... физиологическом механизме внимания также и вегетативных центров. Основные виды внимания При изучении внимания необходимо различать два основных уровня или вида его и ряд его свойств или сторон. Основными видами внимания являются непроизвольное и так называемое произвольное внимание. Непроизвольное внимание связано с рефлекторными установками. Оно устанавливается и поддерживается независимо ...
... этими двумя ветвями так велико, что его невозможно объяснить ошибками в оценке энергии Eg или потерей подпороговых g квантов, или статистическими флуктуациями. Результаты Поперечные импульсы для обоих взаимодействий (с большим и малым PT) были рассчитаны методом факториальных моментов. Из-за удобства и подобных свойств между поперечным импульсом и псевдоскоростью в вычислениях ,была ...
... полуцелые. Существуют правила отбора квантовых чисел атома: ΔL = ± 1,ΔS = 0,ΔJ = 0, ± 1 Магнитный момент атома Как уже говорилось ранее, орбитальный и магнитный моменты электрона связаны гиромагнитным отношением: . Экспериментально было доказано, что для механического и магнитного орбитальных моментов атома выполняется аналогичное соотношение . Подставляя , где L – ...
0 комментариев