Навигация
Разделяя переменные, получаем
8308
знаков
2
таблицы
2
изображения
4.3.8.4. Разделяя переменные, получаем
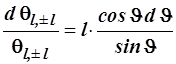(4.115)
Учтём что 
,
(4.116)
Интегрирование уравнения (4.116) даёт
(4.117)
где
– постоянная интегрирования, определяемая из условия нормировки. Окончательно получаем формулу для функции
(4.118)
4.3.8.5.Формула (4.118) дает лишь предельные выражения волновых функций 
, отвечающие максимальному и минимальному значениям квантового числа m, а именно 
и 
, или что то же самое 
. Все волновые функции, соответствующие промежуточным значениям 
очень просто получаются последовательным действием операторов 
с точностью до нормировочных множителей, которые могут быть рассчитаны в каждом конкретном случае
4.3.8.6.Отметим, что мы не ставим перед собой и перед читателем задачу вывода общей формулы сферических волновых функций. Это связано, с одной стороны, с тем, что она обязательно покажется слишком перегруженной индексами и коэффициентами, к которым удобнее привыкать постепенно. С другой стороны, для практических целей редко требуются функции с большими значениями квантового числа l. В химическом обиходе встречается состояния с l = 0, 1, 2, 3, поэтому ограничимся этими значениями, (их символы см. в табл. 4.5 ).
4.3.8.7. Итак, нас будут интересовать s–, p–, d–, f– орбитали жесткого ротатора. Запишем соответствующие исходные функции 
и 
, с точностью до постоянного множителя:
для s-состояния 
и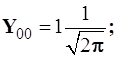 
для p- состояния 
и 
для d- состояния 
и 
для f- состояния 
и 
4.3.8.8.Орбиталь s –типа – лишь одна и волновая пункция 
требует только нормировки. Поскольку сомножитель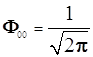 
уже нормирован, достаточно пронормировать функцию 
. Выделяя из элемента конфигурационного пространства 
(см. рис 4.3) все сомножители, определенные на переменной 
, получаем
и, соответственно, нормировочное соотношение имеет вид
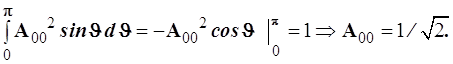(4.119)
Во всех дальнейших преобразованиях следующих двух разделов будем опускать постоянные численные коэффициенты перед волновыми функциями, получающимися в результате операций сдвигов состояний над исходными функциями – степенями синусоиды 
.
4.3.8.9. Квантовое число l=1 порождает три р-функции с m=1, 0, -1 т.е. орбитали с 
Двум из них с 
отвечает 
Нормировочный множитель находим из соотношения
.
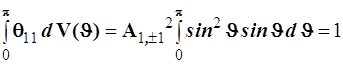Откуда следует: 
(4.120)
Функцию 
, необходимую для полного набора р-орбиталей, можно найти, сдвигая 
вниз или 
вверх на одно состояние
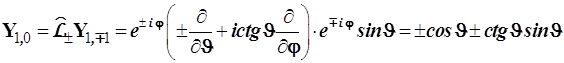
Определим нормировочный множитель 
для
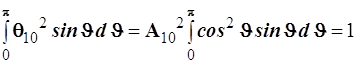
Интегрируя с помощью подстановки 
и, следовательно полагая, 
получаем
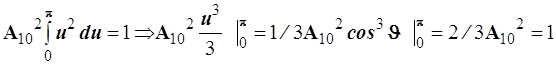, т.е. 
4.3.8.10. Далее получим последовательно d-орбитали, отвечающие набору 
. Соответственно
(4.121)
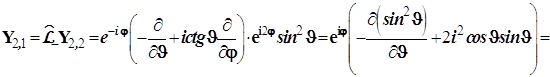
(4.121)
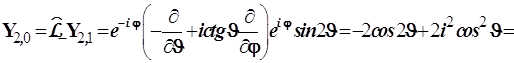
(4.122)
Отсюда получаются d-функции
; 
;
.
Величины 
;
;
представлены в таблице 4.6.
Похожие работы
т вследствие уменьшения момента инерции при сохранении момента вращения. Тут мы и убеждаемся наглядно, что чем меньше момент инерции, тем выше угловая скорость и, как следствие, короче период вращения, обратно пропорциональный ей. 3. Что такое радиоактивность (естественная и искусственная)? Как использование явлений радиоактивности позволило осуществить мечту алхимиков? Радиоактивность (от ...
... физиологическом механизме внимания также и вегетативных центров. Основные виды внимания При изучении внимания необходимо различать два основных уровня или вида его и ряд его свойств или сторон. Основными видами внимания являются непроизвольное и так называемое произвольное внимание. Непроизвольное внимание связано с рефлекторными установками. Оно устанавливается и поддерживается независимо ...
... этими двумя ветвями так велико, что его невозможно объяснить ошибками в оценке энергии Eg или потерей подпороговых g квантов, или статистическими флуктуациями. Результаты Поперечные импульсы для обоих взаимодействий (с большим и малым PT) были рассчитаны методом факториальных моментов. Из-за удобства и подобных свойств между поперечным импульсом и псевдоскоростью в вычислениях ,была ...
... полуцелые. Существуют правила отбора квантовых чисел атома: ΔL = ± 1,ΔS = 0,ΔJ = 0, ± 1 Магнитный момент атома Как уже говорилось ранее, орбитальный и магнитный моменты электрона связаны гиромагнитным отношением: . Экспериментально было доказано, что для механического и магнитного орбитальных моментов атома выполняется аналогичное соотношение . Подставляя , где L – ...
0 комментариев