Навигация
Аналогично получается весь набор f-функций
7069
знаков
2
таблицы
2
изображения
4.3.8.11. Аналогично получается весь набор f-функций
(4.123)
Все найденные s-, р-, d- и f-орбитали сведём в таблицу 4.6.
Таблица 4.6.
Сферические волновые функции
| Уровень | l | m |
|
|
|
| Символ Y |
| s | 0 | 0 | 1 | 1 |
|
|
|
| p | 1 |
|
|
|
| – “ – |
|
| 0 |
| 1 |
| – “ – |
| ||
| d | 2 |
|
|
|
| – “ – |
|
|
|
|
|
| – “ – |
| ||
| 0 |
| 1 |
| – “ – |
| ||
| f | 3 |
|
|
|
| – “ – |
|
|
|
|
|
| – “ – |
| ||
|
|
|
|
| – “ – |
| ||
| 0 |
| 1 |
| – “ – |
|
Полярные диаграммы волновых функций жесткого ротатора.
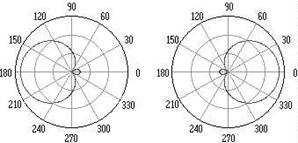
4.3.9.1 В разделе 3.2.7. были рассмотрены полярные диаграммы волновых функций плоского ротатора. Они же – графические образа функции сомножителя 
Теперь проанализируем полярные диаграммы функции 
для чего будем откладывать на радиус-векторе, исходящем из центра под углом 
к оси z, значения функции 
(рис.4.6.).
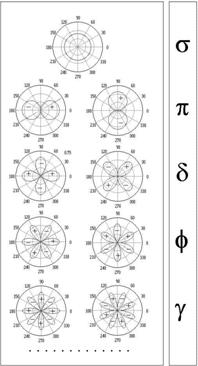
4.3.9.2. В таблице 4.6 суммированы орбитали жесткого ротатора 
с комплексными сомножителями 
которые являются собственными функциями операторов полной энергии, квадрата момента импульса и его проекции на ось z. Однако, графический образ комплексных функций недоступен. На рис. 4.7. представлены полярные диаграммы действительных функций 
, получаемых как линейные комбинации аналогично построенным в разделе 3.2.6 функциям плоского ротатора. При этом, для состояний, описываемых такими действительными функциями утрачивается определенность в значении проекции момента импульса 
, но сохраняется постоянное значение энергии и модуля момента импульса. Как видно на рис. 4.6 и 4.7, число узловых плоскостей на полярных диаграммах равно квантовому числу l . Анализ знаков волновых функций указывает, что орбитали s- и d- являются четными, а p- и f- нечётными по отношению к операции инверсии.
Похожие работы
... лишь угловую часть лапласиана и имеет вид: . (6.23) Уравнение Лежандра, встречается в нескольких фундаментальных задачах: 1) в задаче о квантовых состояниях и энергетических уровнях ротатора - линейной молекулы, свободно вращающейся вокруг центра массы. 2) в уравнении Шрёдингера для атома H и водородоподобных ионов. 6.7.3. Уравнение Лежандра это вполне типичное операторное уравнение на
... решения выберем в виде комплексных экспонент , (3.29) По физическим соображениям можно волновой функции придать вид лишь одного из частных решений. Это связано со свойствами момента импульса в стационарном вращательном движении, которые мы рассмотрим в рамках соответствующего операторного уравнения , т.е. , (3.30) откуда следует, что собственная волновая ...
... калькуляции представлены в табл.4.2. Ленточный график работ 5. Безопасность жизнедеятельности и охрана труда Дипломная работа посвящена анализу погрешностей волоконно-оптического гироскопа. В ходе ее выполнения были проведены необходимые расчеты и сделаны выводы, которые могут послужить материалом для ...
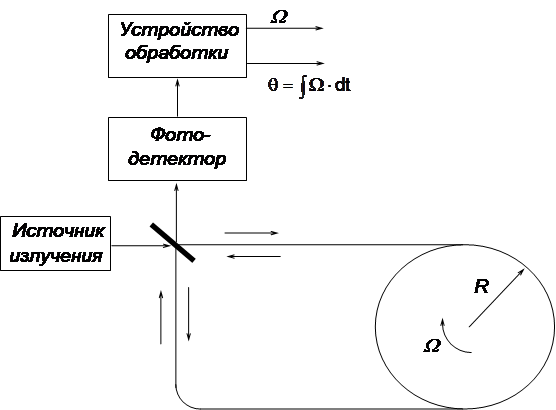
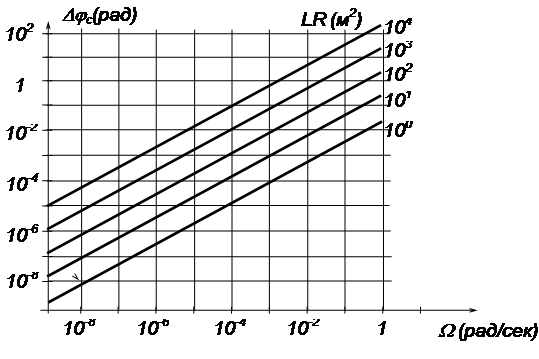
0 комментариев