Навигация
Регрессионный анализ корелляции субъективного ВАШ и лабораторных признаков активности реактивного артрита
Санкт-Петербургский Государственный Университет
Факультет прикладной математики – процессов управления
Кафедра диагностики функциональных систем
Варламова Александра Александровна
Регрессионный анализ корелляции субъективного ВАШ и лабораторных признаков активности реактивного артрита
Заведующий кафедрой
доктор медицинских наук, профессор Шишкин В.И.
Научный руководитель
доктор медицинских наук, профессор Шишкин В.И.
Санкт-Петербург
2008
Содержание
Введение
1 Дисперсионный анализ по одному признаку для проверки равенства нескольких средних
2 Множественная линейная регрессия
3 Дисперсионный анализ
4 Линейная регрессия
Заключение
Введение
Артриты реактивные - термин, принятый для обозначения артритов, развивающихся после инфекций, но не обусловленных попаданием инфекционного агента в полость сустава. Обычно реактивные артриты носят иммунокомплексный характер, т. е. возникают вследствие нарушений иммунитета у генетически предрасположенных лиц из-за недостаточной утилизации комплексов антиген - антитела макрофагальной системой. Реактивные артриты могут развиваться после многих инфекций (бактериальных, вирусных и др. ) независимо от их тяжести, но чаще - после энтероколитов, вызванных иерсиниями, и инфекций мочевых путей, обусловленных хламидиями.
В настоящее время реактивный артрит (РеА) является одним из наиболее частых ревматологических диагнозов. Обычно реактивным считают артрит, который не удовлетворяет диагностическим критериям ревматоидного или подагрического артрита и не сопровождается специфической для системных ревматических заболеваний внесуставной симптоматикой.
Этиология РеА неизвестна. Предположительно, в основе РеА лежит генетически детерминированная аномалия иммунной системы, которая реализуется при инфицировании некоторыми микроорганизмами.
Клиническая картина РеА может включать:
• характерный суставной синдром;
• клинику урогенитальной инфекции;
• внесуставные поражения (кожи и слизистых оболочек);
• поражения позвоночника (обычно сакроилеит);
• висцеральные поражения;
• системную воспалительную реакцию
Суставной синдром (обязательное проявление заболевания) характеризуется:
– асимметричным олигоартритом (воспалением 2-3 суставов или суставных групп) с поражением суставов ног (коленных, голеностопных, плюснефаланговых и межфаланговых) и тендовагинитом (ахиллобурситом);
– началом первого эпизода артрита в период до 30 дней после полового контакта, со средним интервалом в 14 дней между появлением урогенитальных симптомов и артритом;
– болью и ригидностью с отеком или без него в области прикрепления мышц, сухожилий и связок, особенно ахиллова сухожилия и плантарной фасции, к пяточной кости, что часто ведет к затруднениям при ходьбе
Клинические признаки артрита :
1. Боль в суставе/суставах:
• ощущается во всем суставе;
• связана с движениями и суточным ритмом (при любых движениях, усиливается в покое и ночью);
• сопряжена с амплитудой движений в суставе (при движениях во всех плоскостях, нарастающая с увеличением амплитуды движений);
• обычно тупая, ноющая, выкручивающая.
2. Скованность – субъективное ощущение препятствия движению, которое, как правило, наиболее выражено сразу после пробуждения, периода отдыха или неактивности. Скованность обусловлена нарушением оттока жидкости из воспаленного сустава в покое, уменьшается или проходит при возобновлении движений в суставе. Продолжительность и выраженность скованности отражают степень местного воспаления.
3. Припухлость – преходящее увеличение в размерах и изменение контура сустава, обусловленные как накоплением экссудата в полости сустава, так и отеком периартикулярных тканей. Наиболее отчетливо припухлость выявляется на разгибательных (тыльных) поверхностях локтевых и лучезапястных суставов, на кисти, коленных и голеностопных суставах и стопе.
4. Повышение температуры суставов также является признаком воспаления. Определяется проведением тыльной стороной ладони по поверхности сустава.
5. Болезненность сустава при пальпации подтверждает, что боль в суставе обусловлена именно его поражением, а не является отраженной.
Системная воспалительная реакция
Системные симптомы недомогания, усталости, потеря веса и лихорадка встречаются примерно у 10% пациентов. Практические у всех больных в клиническом анализе крови повышена скорость оседания эритроцитов (СОЭ).
Объект, предмет, цель и задача исследованияВ качестве исходных данных для исследования даны выборки численных значений медико-биологических показателей человеческого организма, а именно, показатели активности заболевания : СОЭ, наличие С-реактивного белка, уровня фибриногена и гемоглобина в крови больных реактивным артритом. А также выборка значений болевого синдрома оцененного в баллах по визуальной аналоговой шкале (ВАШБП) и синдрома припухлости (ВАШСП).
В целях полноты изложения приведем необходимые определения :
СОЭ (скорость оседания эритроцитов) - свойство эритроцитов оседать при помещении несвернувшейся крови в вертикально поставленную пробирку. Ускорение наблюдается при большинстве воспалительных, инфекционных и др. заболеваниях.
С-реактивный белок (СРБ) очень чувствительный элемент крови, быстрее других реагирующий на повреждения тканей. Наличие реактивного белка в сыворотке крови – признак воспалительного процесса, травмы, проникновения в организм чужеродных микроорганизмов – бактерий, паразитов, грибов. С-реактивный белок стимулирует защитные реакции, активизирует иммунитет. Определение СБР используется для диагностики острых инфекционных заболеваний и опухолей. Также анализ СРБ используется для контроля над процессом лечения, эффективности антибактериальной терапии и т.д.
Гемоглобин (от гемо... и латинское globus - шар), красный дыхательный пигмент крови человека, позвоночных и некоторых беспозвоночных животных. Состоит из белка (глобина) и железопорфирина - гема. Переносит кислород от органов дыхания к тканям и диоксид углерода от тканей к дыхательным органам. Многие заболевания крови (анемии) связаны с нарушениями строения глобина, в том числе наследственными (гемоглобинопатии - серповидноклеточная анемия, талассемия и др.).
Фибриноген (от фибрин и ...ген), растворимый белок плазмы крови, относящийся к группе глобулинов; фактор I свёртывания крови, способный под действием фермента тромбина превращаться в фибрин. Молекула имеет форму глобулы диаметром около 22 нм. Синтез фибриногена в организме происходит в паренхиматозных клетках печени. Содержание фибриногена в плазме крови здорового человека 300- 500 мг%. При недостаточности фибриногена в организме или при образовании молекул с аномальным строением наблюдается кровоточивость.
ВАШБП - оценка интенсивности боли, для характеристики которой используют простые визуальные аналоговые шкалы.
ВАШСП – оценка припухлости суставов, для характеристики которой используют простые визуальные аналоговые шкалы
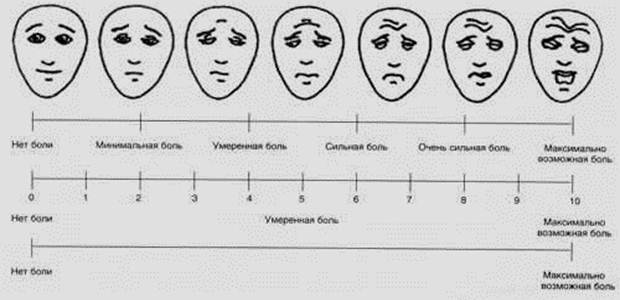
Визуально аналоговые шкалы важный компонент большинства современных клинических методов, применяемых при обследовании пациентов. Специальные опросники позволяют дать более полную характеристику болевого синдрома, выявить связь между выраженностью боли и нарушением функционального состояния больных.
Объект исследования
Объектом нашего исследования являются выборочные данные результатов измерений СОЭ, СРБ, Гемоглобина, Фибриногена, ВАШБП и ВАШСП, причем изучаемые данные разделены на 4 группы. В первой группе представлены данные при болезни, вызванной моче половыми инфекциями, во второй группе - неизвестной этиологии, в третьей – ОРВИ, в четвертой – желудочно-кишечными инфекциями.
Предмет исследования
Предмет исследования определяем, как нахождение зависимости между показателями активности заболевания (СОЭ, СРБ, Фибриноген, Гемоглобин), болевым синдромом оцененным по визуально аналоговой шкале (ВАШБП) и синдромом припухлости оцененным также по визуально аналоговой шкале (ВАШСП).
Используемые методы 1.Дисперсионный анализ по одному признаку для проверки равенства нескольких среднихВо многих случаях практики интерес представляет вопрос о том, в какой мере существенно влияние того или иного фактора на рассматриваемый признак. В данном случае фактором является вид инфекции вызвавший реактивный артрит, а признаками СОЭ, СРБ, Фибриноген, гемоглобин, ВАШБП и ВАШСП. Научное обоснованное решение подобной задачи при некоторых предположениях составляет предмет дисперсионного анализа.
Статистическая модель
Выборки производятся из нормальных совокупностей. Первая выборка производиться из совокупности со средним![]() , вторая - со средним
, вторая - со средним ![]() , k-я из совокупности со средним
, k-я из совокупности со средним ![]() . Все наблюдения независимы.
. Все наблюдения независимы.
Критическая область.
Если значение p![]() 0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выберем критический уровень значимости pKP для условия принятия нулевой гипотезы pкр=0,05
0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выберем критический уровень значимости pKP для условия принятия нулевой гипотезы pкр=0,05
p>pкр
Гипотезы №1.
Н0 : ![]() =
= ![]() =…=
=…= ![]()
Н1: не все средние равны.
Так как данный метод работает только для нормальных совокупностей то сначала построим графики функций распределения для каждой выборки.
Для экономии времени и упрощения расчетов воспользуемся Matlab.
|
График функции распределения для значений Hb в 1 группе |
|
График функции распределения для значений Hb в 2 группе |
|
График функции распределения для значений Hb в 3 группе |
|
График функции распределения для значений Hb в 4 группе |
|
График функции распределения для значений СРБ в 1 группе |
|
График функции распределения для значений СРБ в 2 группе |
|
График функции распределения для значений СРБ в 3 группе |
|
График функции распределения для значений СРБ в 4 группе |
|
График функции распределения для значений СОЭ в 1 группе |
|
График функции распределения для значений СОЭ в 2 группе |
|
График функции распределения для значений СОЭ в 3 группе |
|
График функции распределения для значений СОЭ в 4 группе |
|
График функции распределения для значений Фибриногена в 1 группе |
|
График функции распределения для значений Фибриногена в 2 группе |
|
График функции распределения для значений Фибриногена в 3 группе |
|
График функции распределения для значений Фибриногена в 4 группе |
|
График функции распределения для значений ВАШБП в 1 группе |
|
График функции распределения для значений ВАШБП в 2 группе |
|
График функции распределения для значений ВАШБП в 3 группе |
|
График функции распределения для значений ВАШБП в 4 группе |
|
График функции распределения для значений ВАШСП в 1 группе |
|
График функции распределения для значений ВАШСП в 2 группе |
|
График функции распределения для значений ВАШСП в 3 группе |
|
График функции распределения для значений ВАШСП в 4 группе |
Исходя из вида графиков можно сделать вывод о том что все выборки имеют нормальное распределение и следовательно мы можем использовать выбранный нами параметрический метод дисперсионного анализа.
I) Рассмотрим сначала влияние фактора на уровень Hb (гемоглобин):
Таблица1.1.1.Зависимость уровня Hb от инфекции вызвавшей заболевание
| 1группа | 2группа | 3 группа | 4группа |
| 124 | 114 | 140 | 124 |
| 124 | 142 | 121 | 130 |
| 110 | 156 | 136 | 127 |
| 93 | 170 | 125 | 130 |
| 133 | 119 | 138 | 138 |
| 129 | 128 | 150 | 122 |
| 149 | 163 | 154 | 160 |
| 122 | 135 | 127 | 104 |
| 145 | 120 | 153 | 121 |
| 124 | 120 | 120 | 131 |
| 99 | 106 | 171 | 127 |
| 125 | 130 | 128 | 109 |
| 137 | 156 | 154 | 158 |
| 156 | 114 | 140 | 132 |
| 148 | 137 | 110 | 134 |
| 138 | 142 | 151 | 164 |
| 144 | 121 | 142 | 116 |
| 133 | 121 | 144 | 136 |
| 145 | 144 | 120 | 122 |
| 121 | 160 | 150 | |
| 126 | 140 | 112 | |
| 128 | 110 | 124 | |
| 120 | 135 | 137 | |
| 150 | 106 | 130 | |
| 123 | 126 | 160 | |
| 150 | 136 | 150 | |
| 160 | 142 | 107 | |
| 139 | 118 | 114 | |
| 152 | 126 | 124 | |
| 146 | 140 | 120 | |
| 142 | 101 | 115 | |
| 137 | 123 | ||
| 148 | 117 | ||
| 130 | |||
| 152 | |||
| 126 | |||
| 118 | |||
| 140 | |||
| 166 | |||
| 128 | |||
| 165 | |||
| 143 | |||
| 132 | |||
| 130 | |||
| 126 | |||
| 166 | |||
| 168 | |||
| 128 | |||
| 126 | |||
| 125 | |||
| 115 | |||
| 118 | |||
| 117 | |||
| 114 | |||
| 123 | |||
| 150 | |||
| 125 | |||
| 103 | |||
| 142 | |||
| 150 | |||
| 140 | |||
| 94 | |||
| 129 | |||
| 156 | |||
| 141 | |||
| 148 | |||
| 140 | |||
| 141 | |||
| 135 | |||
| 150 | |||
| 150 | |||
| 127 | |||
| 158 | |||
| 131 | |||
| 150 | |||
| 162 | |||
| 134 | |||
| 104 | |||
| 130 | |||
| 136 | |||
| 150 | |||
| 136 | |||
| 105 | |||
| 146 | |||
| 146 | |||
| 138 | |||
| 158 | |||
| 154 | |||
| 141 | |||
| 134 | |||
| 150 | |||
| 150 | |||
| 114 | |||
| 109 | |||
| 157 | |||
| 161 | |||
| 133 | |||
| 166 | |||
| 168 |
Здесь и далее для экономии времени и упрощения вычислительн6ой работы воспользуемся Matlab для проведения однофакторного дисперсионного анализа для сравнения средних арифметических значений выборок. Будем использовать функцию p = anova1(X) - функция позволяет провести однофакторный дисперсионный анализ для сравнения средних арифметических значений одной или нескольких выборок одинакового объема. Выборки определяются входным аргументом Х. Х задается как матрица с размерностью mxn, где m - число наблюдений в выборке (число строк Х), n - количество выборок (число столбцов матрицы Х). Выходным аргументом функции является уровень значимости p нулевой гипотезы. Нулевая гипотеза состоит в том, что все выборки в матрице Х взяты из одной генеральной совокупности или из разных генеральных совокупностей с равными средними арифметическими. p является вероятностью ошибки первого рода, или вероятностью необоснованно отвергнуть нулевую гипотезу. Если значение p![]() 0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выбор критического уровня значимости pKP для условия принятия нулевой гипотезы
0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выбор критического уровня значимости pKP для условия принятия нулевой гипотезы
![]()
предоставлен исследователю. Здесь и далее примем pKP равным 0,05.
После выполнения вычислений мы получаем:
p = 0.3001
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №1.1.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 1012,4 | 3 | 337,451 |
| Остаточная | 30577,2 | 112 | 273,011 |
| Полная | 31589,5 | 115 | ----- |
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень гемоглобина в крови не зависит от инфекции вызывающей реактивный артрит.
II) Влияние фактора на наличие СРБ в крови
Таблица1.2.1.Зависимость уровня СРБ от инфекции вызвавшей заболевание
| 1 группа | 2 группа | 3 группа | 4 группа |
| 0 | 6 | 0 | 0 |
| 6 | 0 | 0 | 0 |
| 96 | 48 | 0 | 0 |
| 192 | 0 | 0 | 0 |
| 0 | 6 | 12 | 96 |
| 0 | 6 | 12 | 0 |
| 0 | 0 | 6 | 0 |
| 0 | 12 | 0 | 0 |
| 0 | 0 | 0 | 48 |
| 0 | 0 | 48 | 0 |
| 48 | 192 | 0 | 384 |
| 0 | 0 | 0 | 48 |
| 12 | 6 | 0 | 0 |
| 0 | 48 | 0 | 0 |
| 384 | 6 | 12 | 0 |
| 192 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 |
| 48 | 0 | 48 | 0 |
| 0 | 0 | 0 | 0 |
| 96 | 0 | 0 | |
| 0 | 0 | 0 | |
| 48 | 0 | 96 | |
| 0 | 0 | 96 | |
| 12 | 48 | 48 | |
| 6 | 0 | 0 | |
| 6 | 0 | 0 | |
| 0 | 0 | 0 | |
| 96 | 0 | 0 | |
| 48 | 0 | 48 | |
| 6 | 0 | 48 | |
| 0 | 12 | 0 | |
| 0 | 96 | ||
| 0 | 0 | ||
| 0 | |||
| 0 | |||
| 0 | |||
| 768 | |||
| 96 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 12 | |||
| 0 | |||
| 0 | |||
| 6 | |||
| 0 | |||
| 6 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 6 | |||
| 0 | |||
| 0 | |||
| 192 | |||
| 48 | |||
| 0 | |||
| 0 | |||
| 192 | |||
| 768 | |||
| 6 | |||
| 0 | |||
| 96 | |||
| 24 | |||
| 0 | |||
| 6 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 96 | |||
| 48 | |||
| 0 | |||
| 0 | |||
| 48 | |||
| 0 | |||
| 0 | |||
| 6 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 |
После выполнения вычислений мы получаем:
p =0.4677
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №1.2.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 23192,8 | 3 | 7730,92 |
| Остаточная | 1616980,7 | 178 | 9084,16 |
| Полная | 1640173,5 | 181 | ----- |
p>pкр
Вывод:
Следовательно, мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень СРБ в крови не зависит от инфекции вызывающей реактивный артрит.
III) Влияние фактора на СОЭ
Таблица1.3.1.Зависимость СОЭ от инфекции вызвавшей заболевание
| 1 группа | 2 группа | 3 группа | 4 группа |
| 18 | 34 | 10 | 10 |
| 19 | 4 | 21 | 26 |
| 42 | 24 | 3 | 6 |
| 66 | 1 | 7 | 4 |
| 25 | 35 | 22 | 12 |
| 10 | 16 | 26 | 25 |
| 13 | 1 | 12 | 4 |
| 28 | 36 | 6 | 40 |
| 3 | 22 | 1 | 52 |
| 26 | 34 | 18 | 18 |
| 28 | 50 | 1 | 62 |
| 38 | 28 | 2 | 40 |
| 28 | 14 | 4 | 7 |
| 1 | 64 | 10 | 5 |
| 52 | 30 | 23 | 3 |
| 48 | 9 | 2 | 8 |
| 26 | 32 | 10 | 12 |
| 14 | 10 | 17 | 5 |
| 12 | 2 | 15 | 12 |
| 48 | 2 | 12 | |
| 19 | 12 | 10 | |
| 28 | 37 | 30 | |
| 25 | 18 | 24 | |
| 6 | 58 | 40 | |
| 11 | 10 | 2 | |
| 26 | 15 | 2 | |
| 2 | 2 | 8 | |
| 51 | 10 | 5 | |
| 24 | 10 | 10 | |
| 13 | 10 | 35 | |
| 6 | 34 | 39 | |
| 10 | 38 | ||
| 2 | 25 | ||
| 30 | |||
| 2 | |||
| 3 | |||
| 46 | |||
| 56 | |||
| 3 | |||
| 11 | |||
| 4 | |||
| 4 | |||
| 24 | |||
| 11 | |||
| 7 | |||
| 1 | |||
| 7 | |||
| 9 | |||
| 20 | |||
| 14 | |||
| 4 | |||
| 12 | |||
| 17 | |||
| 14 | |||
| 5 | |||
| 2 | |||
| 40 | |||
| 30 | |||
| 6 | |||
| 3 | |||
| 26 | |||
| 69 | |||
| 25 | |||
| 3 | |||
| 35 | |||
| 6 | |||
| 8 | |||
| 3 | |||
| 5 | |||
| 1 | |||
| 5 | |||
| 5 | |||
| 7 | |||
| 6 | |||
| 3 | |||
| 3 | |||
| 5 | |||
| 10 | |||
| 15 | |||
| 3 | |||
| 3 | |||
| 38 | |||
| 49 | |||
| 5 | |||
| 3 | |||
| 19 | |||
| 2 | |||
| 3 | |||
| 10 | |||
| 5 | |||
| 3 | |||
| 5 | |||
| 16 | |||
| 5 | |||
| 4 | |||
| 4 | |||
| 10 | |||
| 1 | |||
| 4 |
После вычислений получаем:
p = 0.0810
Таблица №1.3.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 1658,2 | 3 | 552,744 |
| Остаточная | 43145,7 | 178 | 242,391 |
| Полная | 44803,9 | 181 | ----- |
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости СОЭ не зависит от инфекции вызывающей реактивный артрит.
IV) Влияние фактора на уровень Фибриногена в крови
Таблица1.4.1.Зависимость уровня фибриногена от инфекции вызвавшей заболевание
| 1 группа | 2 группа | 3 группа | 4 группа |
| 3.00 | 5.25 | 6.75 | 2.80 |
| 4.50 | 2.00 | 2.50 | 3.75 |
| 3.50 | 5.75 | 3.10 | 2.50 |
| 7.25 | 2.50 | 3.00 | 3.00 |
| 4.00 | 5.50 | 6.75 | 3.25 |
| 3.25 | 3.50 | 4.50 | 3.50 |
| 5.50 | 3.25 | 3.50 | 3.75 |
| 4.00 | 7.25 | 2.50 | 5.25 |
| 3.25 | 3.75 | 2.50 | 5.10 |
| 5.00 | 3.00 | 4.50 | 4.50 |
| 3.60 | 7.00 | 3.00 | 12.20 |
| 4.25 | 5.50 | 2.15 | 5.75 |
| 4.25 | 4.00 | 2.00 | 5.50 |
| 3.00 | 7.50 | 3.25 | 3.00 |
| 10.20 | 3.50 | 4.25 | 2.50 |
| 4.75 | 4.00 | 2.25 | 3.00 |
| 4.50 | 5.50 | 2.10 | 3.50 |
| 5.00 | 3.25 | 4.75 | 3.00 |
| 5.50 | 2.50 | 3.50 | 2.00 |
| 5.50 | 3.00 | 3.50 | |
| 3.75 | 3.50 | 4.00 | |
| 3.75 | 5.00 | 3.50 | |
| 4.50 | 3.30 | 3.00 | |
| 5.75 | 5.00 | 2.75 | |
| 3.00 | 4.25 | 3.00 | |
| 4.25 | 3.00 | 2.75 | |
| 3.75 | 2.00 | 3.00 | |
| 5.25 | 3.25 | 2.00 | |
| 6.25 | 2.50 | 1.75 | |
| 2.25 | 3.25 | 4.25 | |
| 3.25 | 4.30 | 3.00 | |
| 2.50 | 4.25 | ||
| 2.75 | 4.00 | ||
| 4.00 | |||
| 2.75 | |||
| 4.00 | |||
| 4.50 | |||
| 6.75 | |||
| 3.25 | |||
| 3.75 | |||
| 3.25 | |||
| 4.00 | |||
| 4.25 | |||
| 3.50 | |||
| 2.60 | |||
| 2.75 | |||
| 4.25 | |||
| 2.00 | |||
| 3.75 | |||
| 4.00 | |||
| 4.00 | |||
| 3.00 | |||
| 4.00 | |||
| 3.00 | |||
| 3.20 | |||
| 2.00 | |||
| 8.75 | |||
| 4.00 | |||
| 4.00 | |||
| 5.00 | |||
| 5.00 | |||
| 7.50 | |||
| 4.00 | |||
| 3.25 | |||
| 2.90 | |||
| 3.25 | |||
| 2.90 | |||
| 3.00 | |||
| 2.00 | |||
| 3.00 | |||
| 2.00 | |||
| 2.75 | |||
| 3.00 | |||
| 2.93 | |||
| 4.25 | |||
| 3.00 | |||
| 3.75 | |||
| 4.00 | |||
| 3.00 | |||
| 2.75 | |||
| 2.00 | |||
| 6.00 | |||
| 3.50 | |||
| 3.00 | |||
| 2.50 | |||
| 4.75 | |||
| 3.00 | |||
| 2.75 | |||
| 3.25 | |||
| 2.50 | |||
| 2.00 | |||
| 3.10 | |||
| 2.00 | |||
| 3.25 | |||
| 3.25 | |||
| 3.00 | |||
| 3.25 | |||
| 3.25 | |||
| 4.00 |
После вычислений получаем:
p =0.5494
Таблица №1.4.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 4.733 | 3 | 1.57754 |
| Остаточная | 397.546 | 178 | 2.2334 |
| Полная | 402.278 | 181 | ----- |
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу. т.е. можно предположить что при 5% уровне значимости уровень фибриногена в крови не зависит от инфекции вызывающей реактивный артрит.
V) Влияние фактора на показатель ВАШБП
Таблица 1.5.1.Зависимость ВАШБП от инфекции вызвавшей заболевание
| 1 группа | 2 группа | 3 группа | 4 группа |
| 15 | 25 | 45 | 67 |
| 28 | 25 | 57 | 65 |
| 63 | 35 | 40 | 50 |
| 45 | 33 | 33 | 45 |
| 40 | 65 | 55 | 55 |
| 80 | 45 | 50 | 27 |
| 20 | 50 | 55 | 58 |
| 48 | 25 | 40 | 45 |
| 75 | 45 | 0 | 30 |
| 35 | 44 | 45 | 50 |
| 55 | 100 | 48 | 35 |
| 85 | 65 | 30 | 20 |
| 45 | 55 | 25 | 78 |
| 43 | 64 | 20 | 50 |
| 45 | 15 | 40 | 60 |
| 50 | 15 | 20 | 75 |
| 50 | 40 | 13 | 75 |
| 56 | 28 | 30 | 30 |
| 10 | 15 | 5 | 55 |
| 55 | 25 | 15 | |
| 45 | 17 | 30 | |
| 95 | 70 | 20 | |
| 32 | 45 | 40 | |
| 25 | 55 | 35 | |
| 70 | 40 | 35 | |
| 45 | 10 | 15 | |
| 28 | 5 | 55 | |
| 27 | 25 | 30 | |
| 75 | 10 | 25 | |
| 45 | 2 | 16 | |
| 55 | 35 | 30 | |
| 35 | 60 | ||
| 33 | 45 | ||
| 5 | |||
| 45 | |||
| 35 | |||
| 73 | |||
| 55 | |||
| 56 | |||
| 43 | |||
| 55 | |||
| 20 | |||
| 53 | |||
| 30 | |||
| 55 | |||
| 55 | |||
| 15 | |||
| 70 | |||
| 60 | |||
| 36 | |||
| 20 | |||
| 38 | |||
| 15 | |||
| 53 | |||
| 12 | |||
| 23 | |||
| 40 | |||
| 52 | |||
| 25 | |||
| 0 | |||
| 70 | |||
| 95 | |||
| 25 | |||
| 10 | |||
| 27 | |||
| 40 | |||
| 20 | |||
| 45 | |||
| 15 | |||
| 17 | |||
| 25 | |||
| 25 | |||
| 10 | |||
| 35 | |||
| 70 | |||
| 12 | |||
| 5 | |||
| 38 | |||
| 5 | |||
| 0 | |||
| 5 | |||
| 65 | |||
| 57 | |||
| 5 | |||
| 0 | |||
| 25 | |||
| 5 | |||
| 20 | |||
| 21 | |||
| 5 | |||
| 10 | |||
| 15 | |||
| 15 | |||
| 23 | |||
| 35 | |||
| 3 | |||
| 10 | |||
| 37 |
После вычислений получаем:
p = 0.4569
Таблица №1.5.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 1210.5 | 3 | 403.498 |
| Остаточная | 82391 | 178 | 462.871 |
| Полная | 83601.5 | 181 | ----- |
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу. т.е. можно предположить что при 5% уровне значимости ВАШБП не зависит от инфекции вызывающей реактивный артрит.
VI) Влияние фактора на показатель ВАШСП
Таблица 1.6.1.Зависимость ВАШСП от инфекции вызвавшей заболевание
| 1 группа | 2группа | 3группа | 4группа |
| 20 | 35 | 62 | 70 |
| 53 | 32 | 70 | 78 |
| 68 | 28 | 40 | 41 |
| 55 | 40 | 50 | 30 |
| 43 | 65 | 60 | 60 |
| 75 | 25 | 56 | 40 |
| 12 | 70 | 68 | 60 |
| 40 | 38 | 20 | 42 |
| 67 | 52 | 10 | 83 |
| 38 | 40 | 40 | 53 |
| 80 | 100 | 70 | 70 |
| 80 | 55 | 50 | 51 |
| 41 | 50 | 34 | 70 |
| 65 | 78 | 30 | 80 |
| 50 | 15 | 32 | 70 |
| 48 | 38 | 25 | 80 |
| 45 | 50 | 20 | 75 |
| 50 | 28 | 39 | 30 |
| 25 | 30 | 10 | 19 |
| 40 | 35 | 10 | |
| 55 | 29 | 31 | |
| 89 | 68 | 60 | |
| 60 | 45 | 45 | |
| 25 | 70 | 45 | |
| 70 | 50 | 39 | |
| 50 | 10 | 15 | |
| 50 | 20 | 50 | |
| 55 | 35 | 20 | |
| 55 | 20 | 20 | |
| 60 | 2 | 50 | |
| 55 | 37 | 40 | |
| 40 | 55 | ||
| 32 | 50 | ||
| 40 | |||
| 54 | |||
| 47 | |||
| 80 | |||
| 78 | |||
| 65 | |||
| 50 | |||
| 62 | |||
| 25 | |||
| 52 | |||
| 50 | |||
| 30 | |||
| 60 | |||
| 19 | |||
| 70 | |||
| 70 | |||
| 41 | |||
| 30 | |||
| 43 | |||
| 17 | |||
| 60 | |||
| 15 | |||
| 20 | |||
| 41 | |||
| 43 | |||
| 40 | |||
| 5 | |||
| 80 | |||
| 95 | |||
| 35 | |||
| 20 | |||
| 35 | |||
| 40 | |||
| 48 | |||
| 18 | |||
| 18 | |||
| 40 | |||
| 60 | |||
| 10 | |||
| 20 | |||
| 12 | |||
| 10 | |||
| 50 | |||
| 3 | |||
| 0 | |||
| 5 | |||
| 63 | |||
| 58 | |||
| 10 | |||
| 0 | |||
| 80 | |||
| 10 | |||
| 30 | |||
| 20 | |||
| 5 | |||
| 9 | |||
| 10 | |||
| 40 | |||
| 20 | |||
| 33 | |||
| 5 | |||
| 18 | |||
| 40 | |||
| 15 |
После вычислений получаем:
p = 0.3222
Таблица №1.6.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 1701.7 | 3 | 567.223 |
| Остаточная | 85230.9 | 176 | 484.266 |
| Полная | 86932.5 | 179 | ----- |
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу. т.е. можно предположить что при 5% уровне значимости ВАШСП не зависит от инфекции вызывающей реактивный артрит.
В связи с тем что не один из показателей активности заболевания а также показатели ВАШ не зависят от инфекции предшествующей реактивному артриту дальнейшее разделение данных на группы можно считать не целесообразным.
2 Множественная линейная регрессия
Общее назначение множественной регрессии (этот термин был впервые использован в работе Пирсона - Pearson. 1908) состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной.
В общественных и естественных науках процедуры множественной регрессии чрезвычайно широко используются в исследованиях. В общем. множественная регрессия позволяет исследователю задать вопрос (и. вероятно. получить ответ) о том. "что является лучшим предиктором для...".
Общая вычислительная задача. которую требуется решать при анализе методом множественной регрессии. состоит в подгонке прямой линии к некоторому набору точек.В многомерном случае. когда имеется более одной независимой переменной. линия регрессии не может быть отображена в двумерном пространстве. однако она также может быть легко оценена. В общем случае. процедуры множественной регрессии будут оценивать параметры линейного уравнения вида:
Y = a + b1*X1 + b2*X2 + ... + bp*Xp
Регрессионные коэффициенты (или B-коэффициенты) представляют независимые вклады каждой независимой переменной в предсказание зависимой переменной.
Линия регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимым переменным (X). Однако обычно имеется существенный разброс наблюдаемых точек относительно подогнанной прямой. Отклонение отдельной точки от линии регрессии (от предсказанного значения) называется остатком.
Чем меньше разброс значений остатков около линии регрессии по отношению к общему разбросу значений. тем. очевидно. лучше прогноз. Например. если связь между переменными X и Y отсутствует. то отношение остаточной изменчивости переменной Y к исходной дисперсии равно 1.0. Если X и Y жестко связаны. то остаточная изменчивость отсутствует. и отношение дисперсий будет равно 0.0. В большинстве случаев отношение будет лежать где-то между этими экстремальными значениями. т.е. между 0.0 и 1.0. 1.0 минус это отношение называется R-квадратом или коэффициентом детерминации. Это значение непосредственно интерпретируется следующим образом. Значение R-квадрата является индикатором степени подгонки модели к данным (значение R-квадрата близкое к 1.0 показывает. что модель объясняет почти всю изменчивость соответствующих переменных).
Обычно. степень зависимости двух или более предикторов (независимых переменных или переменных X) с зависимой переменной (Y) выражается с помощью коэффициента множественной корреляции R. По определению он равен корню квадратному из коэффициента детерминации. Это неотрицательная величина. принимающая значения между 0 и 1. Для интерпретации направления связи между переменными смотрят на знаки (плюс или минус) регрессионных коэффициентов или B-коэффициентов. Если B-коэффициент положителен. то связь этой переменной с зависимой переменной положительна; если B-коэффициент отрицателен. то и связь носит отрицательный характер. Конечно. если B-коэффициент равен 0. связь между переменными отсутствует.
Прежде всего. как это видно уже из названия множественной линейной регрессии. предполагается. что связь между переменными является линейной. На практике это предположение. в сущности. никогда не может быть подтверждено; к счастью. процедуры множественного регрессионного анализы в незначительной степени подвержены воздействию малых отклонений от этого предположения.
Основное концептуальное ограничение всех методов регрессионного анализа состоит в том. что они позволяют обнаружить только числовые зависимости. а не лежащие в их основе причинные связи.
Важность анализа остатков. Хотя большинство предположений множественной регрессии нельзя в точности проверить. исследователь может обнаружить отклонения от этих предположений. В частности. выбросы (т.е. экстремальные наблюдения) могут вызвать серьезное смещение оценок. "сдвигая" линию регрессии в определенном направлении и тем самым. вызывая смещение регрессионных коэффициентов. Часто исключение всего одного экстремального наблюдения приводит к совершенно другому результату.
Используя Matlab найдем уравнение множественной регрессии для нахождения зависимости ВАШБП и ВАШСП от других показателей а также найдем коэффициент корреляции для определения зависимости между данными выборками и критерий Фишера для определения уровня доверия к полученному уравнению.
Аппарат множественной линейной регрессии реализуется в Matlab при помощи функции regress. Анализ основывается на нахождении коэффициентов b уравнения вида:
y = b0 + b1x1 + b2x2 + b3x3 + ... + bnxn
Методом наименьших квадратов.
Входными данными для программы будут:
Матрица X по одному измерению равная длине вектора Y (ВАШБП, ВАШСП), а по другому количеству переменных, по которым должна предсказываться переменная “Y” плюс один. Ещё один столбик нам понадобиться для того, чтобы matlab мог по нему рассчитать свободный член уравнения b0, расположен он должен быть первым и заполнен единицами. Т.е. 2-й столбец матрицы X это значения Hb, 3-й столбец значения СОЭ, 4-й значения СРБ и 5-й Фибриноген.
Y – значения ВАШ (ВАШБП, ВАШСП)
Функция regress задается следующим образом:
[b.bint.r.rint.stats] = regress(y.X.0.01)
regress(y.X.0.01) – означает что мы будем искать зависимость Y от Х и с вероятностью 99% коэффициенты b будут принадлежать рассчитанным нами доверительным интервалам.
Выходные данные:
Вектор коэффициентов b.
Матрица bint. содержащая 99% доверительные интервалы для b.
Вектор r (длина которого равна длине Y). содержащий остатки. т.е. разницу между исходными значениями Y. и рассчитанными по полученному уравнению регрессии.
Матрицу rint. содержащую значения 99% доверительного интервала для r
Вектор stats. состоящий из следующих 4 характеристик:
первое значение – коэффициент множественной корреляции R2. показывающий связь исходных данных y и рассчитанных по полученному уравнению. другими словами – это коэффициент. показывающий на сколько хорошо «работает» полученное уравнение. Чем ближе это значение к единице. тем лучше.
второе значение – F-статистика (её ещё называют критерием Фишера).
третье значение – p. табличное значение критерия Фишера при данных степенях свободы. Если критерий Фишера выше этого значения. то уравнению можно верить.
четвёртое значение – оценка дисперсии ошибок
I) рассчитаем уравнение множественной линейной регрессии для ВАШБП
После выполнения расчетов для ВАШБП получили следующие переменные:
| b | bint | r | rint | ||
| 42.1283 | 1.8780 | 82.3786 | -21.9027 | -73.5518 | 29.7465 |
| -0.1015 | -0.3855 | 0.1824 | -10.4547 | -62.2125 | 41.3031 |
| 0.2908 | -0.1418 | 0.7233 | 14.2154 | -36.8404 | 65.2711 |
| 0.0326 | -0.0177 | 0.0829 | -18.2805 | -68.5417 | 31.9806 |
| 0.7105 | -3.0313 | 4.4524 | 1.2654 | -50.5643 | 53.0951 |
| 45.7534 | -5.3326 | 96.8394 | |||
| -14.6868 | -66.0309 | 36.6572 | |||
| 7.2762 | -44.4701 | 59.0225 | |||
| 44.4133 | -6.6808 | 95.5074 | |||
| -5.6498 | -57.3639 | 46.0644 | |||
| 10.6615 | -40.5673 | 61.8902 | |||
| 41.4956 | -9.2270 | 92.2183 | |||
| 5.2307 | -46.4949 | 56.9564 | |||
| 14.2893 | -37.3388 | 65.9175 | |||
| -16.9757 | -64.8977 | 30.9463 | |||
| -1.7014 | -52.3459 | 48.9432 | |||
| 11.3454 | -40.2887 | 62.9794 | |||
| 18.1895 | -33.3589 | 69.7380 | |||
| -24.8022 | -75.9894 | 26.3849 | |||
| 4.1667 | -47.1548 | 55.4881 | |||
| 7.4767 | -44.4040 | 59.3575 | |||
| 53.4995 | 2.7606 | 104.2384 | |||
| -8.4099 | -60.1502 | 43.3304 | |||
| -8.1185 | -59.1222 | 42.8851 | |||
| 34.8356 | -16.4892 | 86.1604 | |||
| 7.3277 | -44.1261 | 58.7815 | |||
| -1.1282 | -52.7224 | 50.4660 | |||
| -22.7002 | -73.0690 | 27.6685 | |||
| 35.3231 | -15.4605 | 86.1067 | |||
| 12.1224 | -39.4234 | 63.6682 | |||
| 23.2364 | -28.4547 | 74.9275 | |||
| 2.0986 | -49.7444 | 53.9416 | |||
| 3.3639 | -48.4351 | 55.1629 | |||
| -35.4930 | -86.7043 | 15.7183 | |||
| 15.7701 | -35.8987 | 67.4389 | |||
| 1.9511 | -49.4156 | 53.3179 | |||
| 1.2643 | -37.9653 | 40.4940 | |||
| 2.8817 | -47.4120 | 53.1755 | |||
| 27.5456 | -23.6290 | 78.7202 | |||
| 8.0058 | -43.8027 | 59.8144 | |||
| 26.1533 | -25.0770 | 77.3836 | |||
| -11.6135 | -63.2959 | 40.0690 | |||
| 14.2769 | -37.5125 | 66.0664 | |||
| -5.0043 | -56.8847 | 46.8760 | |||
| 21.7829 | -29.7810 | 73.3468 | |||
| 27.4824 | -23.6602 | 78.6249 | |||
| -15.3203 | -66.5536 | 35.9129 | |||
| 36.8308 | -14.3416 | 88.0032 | |||
| 21.9905 | -29.7372 | 73.7183 | |||
| -0.3487 | -52.1580 | 51.4607 | |||
| -14.4565 | -65.3638 | 36.4507 | |||
| 2.2326 | -49.4426 | 53.9079 | |||
| -23.0332 | -74.5239 | 28.4574 | |||
| 16.0495 | -35.4532 | 67.5522 | |||
| -21.3666 | -72.7803 | 30.0472 | |||
| -5.9001 | -57.5397 | 45.7395 | |||
| -13.5376 | -63.5547 | 36.4796 | |||
| 7.2019 | -44.2296 | 58.6334 | |||
| -7.2965 | -59.0702 | 44.4772 | |||
| -31.3225 | -82.2665 | 19.6215 | |||
| 24.7206 | -26.5090 | 75.9502 | |||
| 12.0085 | -29.4721 | 53.4890 | |||
| -14.3362 | -66.1232 | 37.4507 | |||
| -19.4698 | -71.0521 | 32.1125 | |||
| -16.1754 | -66.8306 | 34.4799 | |||
| 8.0639 | -43.7532 | 59.8809 | |||
| -12.2995 | -64.1466 | 39.5476 | |||
| 13.9893 | -37.7707 | 65.7493 | |||
| -16.2954 | -67.9216 | 35.3308 | |||
| -12.3199 | -64.0425 | 39.4027 | |||
| -4.7723 | -56.3885 | 46.8438 | |||
| -7.6406 | -59.3361 | 44.0548 | |||
| -20.2521 | -71.7464 | 31.2422 | |||
| 2.3469 | -49.4690 | 54.1627 | |||
| 39.2104 | -11.8405 | 90.2614 | |||
| -16.6829 | -68.1490 | 34.7832 | |||
| -27.6404 | -79.0945 | 23.8136 | |||
| 0.6820 | -50.1330 | 51.4970 | |||
| -30.4212 | -81.9717 | 21.1294 | |||
| -31.1453 | -82.5884 | 20.2978 | |||
| -24.1908 | -75.6191 | 27.2374 | |||
| 18.2420 | -33.1537 | 69.6377 | |||
| 7.2360 | -43.3212 | 57.7931 | |||
| -25.8891 | -77.5028 | 25.7247 | |||
| -29.9523 | -81.4193 | 21.5148 | |||
| -13.5789 | -65.3925 | 38.2347 | |||
| -23.7983 | -75.2594 | 27.6627 | |||
| -9.3176 | -61.0193 | 42.3841 | |||
| -12.2236 | -64.0984 | 39.6512 | |||
| -26.7522 | -78.2955 | 24.7910 | |||
| -19.1908 | -70.7002 | 32.3185 | |||
| -15.5540 | -67.2924 | 36.1844 | |||
| -21.6260 | -72.8683 | 29.6163 | |||
| -11.8236 | -62.7620 | 39.1148 | |||
| 5.3410 | -46.3573 | 57.0393 | |||
| -26.0752 | -77.4141 | 25.2636 | |||
| -23.8405 | -75.5436 | 27.8627 | |||
| 9.1271 | -42.3050 | 60.5592 | |||
| -22.0750 | -73.2466 | 29.0966 | |||
| -19.3643 | -70.7356 | 32.0071 | |||
| -5.2939 | -57.0079 | 46.4201 | |||
| -3.9155 | -55.2281 | 47.3971 | |||
| 6.0662 | -45.1461 | 57.2784 | |||
| 20.6750 | -30.6746 | 72.0246 | |||
| 8.5343 | -43.3618 | 60.4303 | |||
| 21.8225 | -29.5504 | 73.1954 | |||
| -19.4300 | -70.1039 | 31.2439 | |||
| 5.9953 | -45.8101 | 57.8006 | |||
| 2.0391 | -49.2100 | 53.2883 | |||
| 42.8692 | -7.4532 | 93.1915 | |||
| 24.0227 | -27.3822 | 75.4275 | |||
| 21.6036 | -29.8883 | 73.0954 | |||
| 7.9463 | -42.0260 | 57.9186 | |||
| -24.6224 | -75.8610 | 26.6162 | |||
| -18.1688 | -69.9114 | 33.5739 | |||
| -3.0542 | -54.5917 | 48.4834 | |||
| -7.0589 | -58.7440 | 44.6261 | |||
| -14.8646 | -66.5830 | 36.8538 | |||
| -3.5953 | -55.2165 | 48.0260 | |||
| -16.8888 | -68.7256 | 34.9480 | |||
| 24.7304 | -26.4446 | 75.9054 | |||
| 9.0011 | -42.8700 | 60.8722 | |||
| 1.6549 | -48.7937 | 52.1035 | |||
| 4.7382 | -46.8959 | 56.3724 | |||
| -24.8120 | -76.4793 | 26.8554 | |||
| -24.7124 | -76.2026 | 26.7778 | |||
| -10.3635 | -61.9389 | 41.2118 | |||
| -24.0183 | -75.5760 | 27.5393 | |||
| -31.1297 | -82.7024 | 20.4430 | |||
| -10.2047 | -61.4757 | 41.0663 | |||
| 13.1655 | -38.3588 | 64.6897 | |||
| 4.6407 | -47.1058 | 56.3873 | |||
| 9.3834 | -40.9519 | 59.7187 | |||
| 19.2757 | -32.2076 | 70.7590 | |||
| 8.6060 | -43.1614 | 60.3735 | |||
| -0.6029 | -52.3315 | 51.1257 | |||
| 15.3004 | -35.5974 | 66.1982 | |||
| 11.9546 | -39.5044 | 63.4137 | |||
| 22.3373 | -29.2132 | 73.8877 | |||
| 7.2462 | -44.4642 | 58.9567 | |||
| -28.6600 | -80.0657 | 22.7457 | |||
| 5.0618 | -46.6397 | 56.7633 | |||
| 20.8124 | -30.2927 | 71.9175 | |||
| -1.2405 | -52.8524 | 50.3713 | |||
| -4.0754 | -55.6256 | 47.4747 | |||
| -13.1297 | -64.9991 | 38.7397 | |||
| -1.0570 | -52.6293 | 50.5152 | |||
| -8.9762 | -60.6462 | 42.6938 | |||
| -19.1095 | -70.6665 | 32.4476 | |||
| -7.3882 | -59.1979 | 44.4216 | |||
| -31.7918 | -83.1929 | 19.6092 | |||
| 32.5654 | -18.8114 | 83.9423 | |||
| 25.8476 | -25.6974 | 77.3926 | |||
| 17.2462 | -34.3729 | 68.8654 | |||
| 12.7771 | -38.9022 | 64.4564 | |||
| 17.9586 | -33.6785 | 69.5957 | |||
| -12.4963 | -64.2189 | 39.2263 | |||
| 28.2903 | -23.0283 | 79.6090 | |||
| -1.9287 | -53.1104 | 49.2530 | |||
| -20.1486 | -70.8255 | 30.5284 | |||
| 12.7423 | -39.0574 | 64.5419 | |||
| -33.4366 | -79.4435 | 12.5702 | |||
| -28.3399 | -79.4332 | 22.7535 | |||
| 45.9715 | -4.3766 | 96.3197 | |||
| 17.6894 | -33.9998 | 69.3786 | |||
| 28.8293 | -22.6317 | 80.2902 | |||
| 45.0664 | -5.5918 | 95.7246 | |||
| 38.6743 | -12.3544 | 89.7029 | |||
| -1.9044 | -53.7565 | 49.9477 | |||
| 20.3493 | -31.0914 | 71.7901 | |||
| -17.8734 | -69.5782 | 33.8313 | |||
| -6.5057 | -57.7216 | 44.7103 | |||
| -23.8741 | -75.3281 | 27.5800 | |||
| -0.4543 | -52.0199 | 51.1113 | |||
| -9.0759 | -59.6117 | 41.4599 | |||
| 6.4047 | -45.2060 | 58.0155 | |||
| -14.4330 | -66.1409 | 37.2749 | |||
| 19.2787 | -31.6829 | 70.2403 | |||
| -3.4277 | -54.6947 | 47.8392 | |||
| -10.2520 | -61.6535 | 41.1494 | |||
| -28.7033 | -80.0804 | 22.6737 | |||
| -13.9223 | -64.7794 | 36.9348 | |||
stats = 0.1569; 8.2341; 0.0000; 398.2227;
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШБП= 42.1283 – 0.1015 Hb + 0.2908 СОЭ + 0.0326 СРБ +0.7105 Фибриноген
R2=0.1569 - 15.69% от исходной изменчивости могут быть объяснены. а 84.31% остаточной изменчивости остаются необъясненными.
F=8.2341
p= 0
F>p следовательно полученному уравнению можно верить с вероятностью в 99%
Далее произведем анализ остатков и исключим из выборки экстремальные наблюдения. а затем заново рассчитаем уравнение множественной регрессии.
После вычислений получаем новые переменные и новое уравнение:
| b | bint | r | rint | ||
| 68.6128 | 42.6275 | 94.5981 | -9.0527 | -37.3058 | 19.2004 |
| -0.3179 | -0.4996 | -0.1362 | 12.6863 | -14.9838 | 40.3564 |
| 0.2660 | 0.0000 | 0.5319 | 4.7180 | -23.6375 | 33.0735 |
| 0.0363 | 0.0073 | 0.0653 | -7.8665 | -35.8002 | 20.0673 |
| 0.5753 | -1.9305 | 3.0812 | 8.4230 | -19.8230 | 36.6691 |
| -3.9845 | -32.2508 | 24.2819 | |||
| 6.5985 | -21.2655 | 34.4624 | |||
| 9.6122 | -18.6033 | 37.8276 | |||
| -10.2044 | -35.0328 | 14.6240 | |||
| 2.7871 | -24.8193 | 30.3934 | |||
| 17.2257 | -10.7195 | 45.1709 | |||
| 5.4367 | -22.5254 | 33.3988 | |||
| 9.2325 | -19.0964 | 37.5614 | |||
| -7.7024 | -35.9560 | 20.5512 | |||
| -1.2661 | -28.9378 | 26.4056 | |||
| 14.4948 | -13.4018 | 42.3914 | |||
| 7.5633 | -20.5114 | 35.6379 | |||
| -17.4951 | -44.6647 | 9.6746 | |||
| 17.8317 | -9.9962 | 45.6596 | |||
| 5.8425 | -22.4781 | 34.1631 | |||
| 9.3237 | -18.9007 | 37.5480 | |||
| 3.3445 | -24.6908 | 31.3798 | |||
| -0.8088 | -21.5731 | 19.9554 | |||
| 8.6299 | -18.5165 | 35.7762 | |||
| 9.9962 | -18.2684 | 38.2609 | |||
| -6.5170 | -34.7503 | 21.7163 | |||
| 17.5223 | -10.5451 | 45.5896 | |||
| -2.6598 | -31.0639 | 25.7443 | |||
| -4.7289 | -32.6182 | 23.1603 | |||
| 1.1007 | -27.2539 | 29.4553 | |||
| -15.4184 | -42.9371 | 12.1002 | |||
| 1.9826 | -26.2594 | 30.2246 | |||
| 14.9612 | -12.9779 | 42.9002 | |||
| 0.3910 | -27.7965 | 28.5784 | |||
| -11.5190 | -38.0908 | 15.0528 | |||
| 4.1080 | -23.9282 | 32.1441 | |||
| -2.3669 | -30.6874 | 25.9536 | |||
| 5.7176 | -16.0196 | 27.4548 | |||
| -11.7715 | -40.0204 | 16.4775 | |||
| -11.6867 | -39.7871 | 16.4137 | |||
| -11.2514 | -38.7594 | 16.2566 | |||
| 14.1006 | -14.0387 | 42.2399 | |||
| -7.9019 | -36.2419 | 20.4382 | |||
| 18.4706 | -9.5140 | 46.4553 | |||
| -13.1757 | -41.2401 | 14.8888 | |||
| -5.9183 | -34.1797 | 22.3430 | |||
| 1.5930 | -26.5748 | 29.7608 | |||
| -6.1504 | -34.3885 | 22.0877 | |||
| -11.9710 | -40.0136 | 16.0715 | |||
| 4.7517 | -23.5772 | 33.0805 | |||
| -7.6354 | -35.6957 | 20.4249 | |||
| -2.5114 | -30.1466 | 25.1238 | |||
| -17.8750 | -45.7099 | 9.9598 | |||
| 4.9776 | -22.4033 | 32.3584 | |||
| -9.2707 | -37.5638 | 19.0224 | |||
| -15.6411 | -43.5795 | 12.2973 | |||
| -2.0349 | -30.2891 | 26.2193 | |||
| -7.5352 | -35.9057 | 20.8354 | |||
| -12.8750 | -40.8787 | 15.1286 | |||
| -9.0399 | -37.2915 | 19.2118 | |||
| -14.1604 | -41.7111 | 13.3903 | |||
| 13.3652 | -14.6783 | 41.4087 | |||
| -17.2193 | -45.0403 | 10.6016 | |||
| 19.0244 | -8.6055 | 46.6542 | |||
| -11.5693 | -39.3592 | 16.2207 | |||
| -19.6532 | -47.3414 | 8.0351 | |||
| -0.6843 | -28.9330 | 27.5644 | |||
| 4.5464 | -23.3429 | 32.4356 | |||
| 16.7275 | -10.8084 | 44.2634 | |||
| 10.5922 | -17.7215 | 38.9060 | |||
| -14.8775 | -42.1330 | 12.3780 | |||
| 6.5270 | -21.7825 | 34.8365 | |||
| 2.7666 | -25.1568 | 30.6900 | |||
| 8.5476 | -18.2907 | 35.3860 | |||
| -13.1649 | -41.3581 | 15.0284 | |||
| -1.8218 | -29.9553 | 26.3117 | |||
| -6.6755 | -34.9033 | 21.5523 | |||
| -9.8041 | -38.0180 | 18.4097 | |||
| 4.9947 | -23.1450 | 33.1345 | |||
| -12.3110 | -40.5921 | 15.9700 | |||
| 12.6185 | -15.6296 | 40.8666 | |||
| 0.0386 | -27.2984 | 27.3755 | |||
| 6.3388 | -21.8537 | 34.5312 | |||
| -10.6292 | -38.7183 | 17.4599 | |||
| -13.4573 | -41.1993 | 14.2847 | |||
| 14.4516 | -13.5325 | 42.4357 | |||
| 4.6315 | -23.6516 | 32.9145 | |||
| 14.3512 | -12.5735 | 41.2759 | |||
| 12.0414 | -16.1382 | 40.2210 | |||
| 0.5380 | -27.7541 | 28.8300 | |||
| 20.0878 | -7.0899 | 47.2654 | |||
| 19.1331 | -8.6111 | 46.8774 | |||
| 8.7274 | -19.4685 | 36.9234 | |||
| 5.4167 | -22.8281 | 33.6615 | |||
| 0.3107 | -27.8741 | 28.4954 | |||
| 3.1306 | -24.9738 | 31.2350 | |||
| -8.6352 | -36.9898 | 19.7193 | |||
| -2.6414 | -30.7999 | 25.5171 | |||
| -2.4350 | -30.6568 | 25.7869 | |||
| -14.3378 | -42.3473 | 13.6717 | |||
| -1.8313 | -30.1660 | 26.5034 | |||
| 18.7274 | -9.1685 | 46.6234 | |||
| 14.9255 | -13.1336 | 42.9846 | |||
| -11.4913 | -39.6756 | 16.6930 | |||
| -4.2104 | -32.0433 | 23.6225 | |||
| -18.6544 | -45.9305 | 8.6218 | |||
| 15.6565 | -12.4643 | 43.7773 | |||
| 1.5669 | -26.8071 | 29.9410 | |||
| -11.1319 | -39.3470 | 17.0832 | |||
| -7.9681 | -35.8440 | 19.9077 | |||
| 3.3454 | -24.8477 | 31.5384 | |||
| -6.2493 | -33.6830 | 21.1844 | |||
| 14.9947 | -12.9265 | 42.9160 | |||
| -8.0405 | -36.2726 | 20.1915 | |||
| 16.5496 | -10.9807 | 44.0799 | |||
| -4.8517 | -32.7475 | 23.0440 | |||
| -9.6016 | -37.5465 | 18.3433 | |||
| -14.1529 | -41.6157 | 13.3098 | |||
stats = 0.5231; 30.9919; 0; 118.0091;
ВАШБП= 68.6128 – 0.3179 Hb + 0.2660 СОЭ + 0.0363 СРБ +0.5753 Фибриноген
R2=0.5231 - 52.31% от исходной изменчивости могут быть объяснены. а 47.69% остаточной изменчивости остаются необъясненными.
F=30.9919
p= 0
F>p следовательно полученному уравнению можно верить.
Исключая и далее экстремальные наблюдения. возможно построить уравнение объясняющее еще больший процент изменчивости переменной Y (ВАШБП).
Построенное уравнение показывает что наилучшим предсказывающим фактором (предиктором) для ВАШБП является Фибриноген.
II) рассчитаем уравнение множественной линейной регрессии для ВАШСП
После выполнения расчетов для ВАШСП получаем:
| b | bint | r | rint | |||
| 34.4446 | -5.3696 | 74.2588 | -22.0047 | -73.0438 | 29.0343 | |
| -0.0248 | -0.3063 | 0.2567 | 9.4034 | -41.7566 | 60.5635 | |
| 0.4860 | 0.0556 | 0.9164 | 11.0867 | -39.4013 | 61.5746 | |
| 0.0269 | -0.0230 | 0.0768 | -18.9427 | -68.5986 | 30.7132 | |
| 0.6296 | -3.0822 | 4.3415 | -2.8132 | -54.0347 | 48.4083 | |
| 36.8501 | -13.8945 | 87.5948 | ||||
| -28.5283 | -79.0411 | 21.9845 | ||||
| -7.5443 | -58.6841 | 43.5956 | ||||
| 32.6494 | -18.1678 | 83.4666 | ||||
| -9.1522 | -60.2423 | 41.9378 | ||||
| 30.8460 | -19.4622 | 81.1541 | ||||
| 27.5125 | -22.9630 | 77.9879 | ||||
| -6.6522 | -57.7655 | 44.4612 | ||||
| 32.0518 | -18.6502 | 82.7538 | ||||
| -22.7943 | -70.0647 | 24.4762 | ||||
| -14.5034 | -64.4720 | 35.4653 | ||||
| -1.6638 | -52.7402 | 49.4126 | ||||
| 7.6126 | -43.4318 | 58.6569 | ||||
| -15.1416 | -65.8714 | 35.5883 | ||||
| -20.8158 | -71.3764 | 29.7448 | ||||
| 12.0866 | -39.1543 | 63.3276 | ||||
| 40.4712 | -10.1110 | 91.0534 | ||||
| 13.5493 | -37.5432 | 64.6418 | ||||
| -12.5814 | -62.9502 | 37.7874 | ||||
| 31.2113 | -19.5904 | 82.0130 | ||||
| 3.8039 | -47.0594 | 54.6671 | ||||
| 16.1928 | -34.6959 | 67.0816 | ||||
| -6.6698 | -56.6177 | 43.2782 | ||||
| 7.4368 | -43.2022 | 58.0757 | ||||
| 21.2822 | -29.5356 | 72.1001 | ||||
| 19.1169 | -32.0283 | 70.2620 | ||||
| 2.5209 | -48.7140 | 53.7558 | ||||
| -1.4753 | -52.6685 | 49.7179 | ||||
| -8.3178 | -59.3686 | 42.7330 | ||||
| 20.6240 | -30.3657 | 71.6137 | ||||
| 11.7056 | -39.0037 | 62.4150 | ||||
| 2.6396 | -36.0613 | 41.3405 | ||||
| 12.9805 | -36.6568 | 62.6177 | ||||
| 31.1705 | -19.3079 | 81.6490 | ||||
| 11.0245 | -40.1560 | 62.2050 | ||||
| 27.6597 | -22.9260 | 78.2454 | ||||
| -10.3585 | -61.4439 | 40.7269 | ||||
| 6.4906 | -44.7533 | 57.7345 | ||||
| 10.9088 | -40.3295 | 62.1471 | ||||
| -6.3570 | -57.4778 | 44.7639 | ||||
| 27.4574 | -23.0693 | 77.9842 | ||||
| -17.5149 | -68.1171 | 33.0872 | ||||
| 33.0984 | -17.5583 | 83.7551 | ||||
| 26.4393 | -24.5970 | 77.4755 | ||||
| 0.3345 | -50.8698 | 51.5388 | ||||
| -6.0534 | -56.4208 | 44.3141 | ||||
| 3.7625 | -47.3066 | 54.8317 | ||||
| -25.3221 | -76.1620 | 25.5178 | ||||
| 19.5298 | -31.3220 | 70.3816 | ||||
| -20.8371 | -71.6505 | 29.9762 | ||||
| -12.9534 | -63.9315 | 38.0246 | ||||
| -20.4564 | -69.7872 | 28.8745 | ||||
| -7.2787 | -58.1104 | 43.5530 | ||||
| 3.6446 | -47.5376 | 54.8268 | ||||
| -30.3284 | -80.6854 | 20.0286 | ||||
| 28.0814 | -22.4730 | 78.6359 | ||||
| 3.9765 | -37.0488 | 45.0017 | ||||
| -11.0738 | -62.2851 | 40.1374 | ||||
| -14.0776 | -65.1176 | 36.9624 | ||||
| -17.3640 | -67.3964 | 32.6683 | ||||
| 3.6203 | -47.6074 | 54.8481 | ||||
| 13.6091 | -37.5453 | 64.7636 | ||||
| -17.4134 | -68.5347 | 33.7079 | ||||
| -14.4674 | -65.4316 | 36.4968 | ||||
| 4.9588 | -46.2466 | 56.1643 | ||||
| 25.0177 | -25.7733 | 75.8087 | ||||
| -25.8147 | -76.5983 | 24.9690 | ||||
| -15.9546 | -67.0693 | 35.1600 | ||||
| -22.5584 | -73.2294 | 28.1126 | ||||
| -25.9105 | -76.7866 | 24.9657 | ||||
| 10.7575 | -39.4114 | 60.9264 | ||||
| -37.3978 | -88.1530 | 13.3575 | ||||
| -34.2591 | -85.0080 | 16.4898 | ||||
| -28.4395 | -79.1662 | 22.2873 | ||||
| 7.1019 | -43.8000 | 58.0038 | ||||
| -1.1487 | -51.1280 | 48.8305 | ||||
| -25.1404 | -76.1545 | 25.8736 | ||||
| -33.8536 | -84.6079 | 16.9008 | ||||
| 35.4639 | -15.3332 | 86.2611 | ||||
| -23.3846 | -74.2392 | 27.4701 | ||||
| -3.8124 | -54.9315 | 47.3066 | ||||
| -18.0134 | -69.2128 | 33.1859 | ||||
| -30.1234 | -80.9801 | 20.7333 | ||||
| -24.4395 | -75.2474 | 26.3685 | ||||
| -25.1041 | -76.0837 | 25.8755 | ||||
| -0.6512 | -51.4711 | 50.1687 | ||||
| -16.2161 | -66.5045 | 34.0724 | ||||
| -1.5388 | -52.6389 | 49.5613 | ||||
| -29.2822 | -79.9380 | 21.3737 | ||||
| -20.0506 | -71.2057 | 31.1045 | ||||
| 7.1426 | -43.6939 | 57.9791 | ||||
| -19.7381 | -70.3403 | 30.8641 | ||||
| -16.6074 | -67.4100 | 34.1953 | ||||
| -2.1240 | -53.2381 | 48.9901 | ||||
| -19.1491 | -69.7304 | 31.4321 | ||||
| 7.7141 | -42.8786 | 58.3068 | ||||
| 12.8733 | -37.9695 | 63.7160 | ||||
| -16.4096 | -67.6248 | 34.8056 | ||||
| 37.0681 | -13.3471 | 87.4834 | ||||
| -15.4789 | -65.6088 | 34.6509 | ||||
| 7.4797 | -43.7139 | 58.6732 | ||||
| -9.8804 | -60.4900 | 40.7292 | ||||
| 34.3137 | -15.6535 | 84.2810 | ||||
| 6.7098 | -44.2910 | 57.7105 | ||||
| 9.9425 | -41.0808 | 60.9658 | ||||
| 9.2656 | -40.0972 | 58.6285 | ||||
| -32.9906 | -83.4306 | 17.4494 | ||||
| 0.1865 | -51.0727 | 51.4458 | ||||
| -0.4577 | -51.3953 | 50.4799 | ||||
| -10.3484 | -61.4071 | 40.7103 | ||||
| -3.4172 | -54.6044 | 47.7701 | ||||
| 1.6651 | -49.3512 | 52.6814 | ||||
| -10.0063 | -61.3041 | 41.2914 | ||||
| 15.1540 | -35.5594 | 65.8675 | ||||
| 3.0794 | -48.2116 | 54.3703 | ||||
| 5.5574 | -44.2786 | 55.3934 | ||||
| 11.1460 | -39.8436 | 62.1357 | ||||
| -30.2489 | -81.1894 | 20.6917 | ||||
| -13.1520 | -64.1954 | 37.8915 | ||||
| -3.4228 | -54.4306 | 47.5849 | ||||
| -17.7521 | -68.8004 | 33.2962 | ||||
| -35.8769 | -86.7118 | 14.9581 | ||||
| -14.4932 | -65.1229 | 36.1365 | ||||
| -0.1188 | -51.1060 | 50.8683 | ||||
| 3.7897 | -47.3559 | 54.9354 | ||||
| 21.9194 | -27.6652 | 71.5039 | ||||
| 26.7776 | -23.9676 | 77.5227 | ||||
| 5.5205 | -45.6555 | 56.6965 | ||||
| 13.3664 | -37.6893 | 64.4221 | ||||
| 13.7147 | -36.6026 | 64.0320 | ||||
| 9.4851 | -41.3890 | 60.3592 | ||||
| 29.1797 | -21.6240 | 79.9835 | ||||
| -15.7831 | -66.8133 | 35.2470 | ||||
| -22.7078 | -73.6132 | 28.1977 | ||||
| -4.3393 | -55.4381 | 46.7594 | ||||
| 37.4241 | -12.6945 | 87.5427 | ||||
| 16.4062 | -34.4985 | 67.3108 | ||||
| 0.1738 | -50.7715 | 51.1190 | ||||
| -7.8769 | -59.1793 | 43.4256 | ||||
| -13.8921 | -64.7886 | 37.0044 | ||||
| -8.0860 | -59.1509 | 42.9788 | ||||
| -17.1031 | -68.0762 | 33.8699 | ||||
| -4.4151 | -55.6334 | 46.8032 | ||||
| -30.9607 | -81.7690 | 19.8475 | ||||
| 32.0094 | -18.7677 | 82.7865 | ||||
| 31.7837 | -19.0185 | 82.5860 | ||||
| 5.2169 | -45.8980 | 56.3317 | ||||
| -5.0515 | -56.1756 | 46.0727 | ||||
| 18.5197 | -32.4990 | 69.5385 | ||||
| -5.7714 | -56.9352 | 45.3925 | ||||
| 25.2208 | -25.5482 | 75.9898 | ||||
| -12.6104 | -63.1297 | 37.9090 | ||||
| 21.7828 | -28.2603 | 71.8259 | ||||
| 10.2245 | -40.9908 | 61.4398 | ||||
| -9.4350 | -55.3153 | 36.4453 | ||||
| -5.0919 | -55.8748 | 45.6909 | ||||
| 32.6112 | -17.5312 | 82.7536 | ||||
| 44.5121 | -5.9272 | 94.9515 | ||||
| 35.8486 | -14.8237 | 86.5210 | ||||
| 43.8482 | -6.2251 | 93.9214 | ||||
| 35.3981 | -15.1079 | 85.9040 | ||||
| -5.3886 | -56.6237 | 45.8465 | ||||
| -19.5086 | -70.3569 | 31.3398 | ||||
| -28.7582 | -79.6589 | 22.1426 | ||||
| -8.0440 | -58.6477 | 42.5597 | ||||
| 9.2664 | -41.7655 | 60.2984 | ||||
| -2.1800 | -53.1386 | 48.7786 | ||||
| -8.6818 | -58.6147 | 41.2510 | ||||
| 5.6651 | -45.3400 | 56.6702 | ||||
| -18.4257 | -69.4724 | 32.6210 | ||||
| 12.4336 | -38.0096 | 62.8769 | ||||
| -15.3049 | -65.8878 | 35.2780 | ||||
| -17.3295 | -68.1602 | 33.5013 | ||||
| -2.4444 | -53.5238 | 48.6351 | ||||
| -13.7255 | -64.1018 | 36.6508 | ||||
stats = 0.2171 12.1355 0.0000 388.8866
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШСП= 34.4446 – 0.0248 Hb + 0.4860 СОЭ + 0.0269 СРБ +0.6 296Фибриноген
R2=0.2171 - 21.71% от исходной изменчивости могут быть объяснены
F=12.1355
p= 0
F>p следовательно полученному уравнению можно верить.
Далее произведем анализ остатков и исключим из выборки экстремальные наблюдения. а затем заново рассчитаем уравнение множественной регрессии.
Новое уравнение будет выглядеть следующим образом:
ВАШСП= 32.6943 – 0.0638 Hb + 0.4418 СОЭ + 0.0269 СРБ +1.9637 Фибриноген
stats =0.5550; 34.9170; 0; 111.2369;
R2=0.5550 - 55.50% от исходной изменчивости могут быть объяснены
F=34.9170
p= 0
F>p следовательно полученному уравнению можно верить.
Вывод: исходя из полученного уравнения, можно сделать вывод о том, что наилучшим предсказывающим фактором для ВАШСП является фибриноген.
Зависимость ВАШБП и ВАШСП от показателей активности в динамикеРазобьем наши данные на три группы. В первую группу войдут данные полученные до лечения. во вторую данные после 2 месяцев лечения а в третью после трех месяцев.
Так как ранее мы уже проводили исследование на проверку распределения выборок то мы можем воспользоваться параметрическим методом дисперсионного анализа для проверки различий средних. Проверка необходима для подтверждения целесообразности разделения данных, если это подтвердится, то затем мы рассчитаем для каждой группы уравнение зависимости ВАШСП и ВАШБП от показателей активности заболевания.
3 Дисперсионный анализ
Таблица 2.1.1. Зависимость Hb от стадии лечения
| 1 группа | 2 группа | 3 группа |
| 124 | 125 | 134 |
| 124 | 115 | 104 |
| 110 | 118 | 130 |
| 93 | 117 | 136 |
| 133 | 114 | 150 |
| 129 | 123 | 136 |
| 149 | 150 | 105 |
| 122 | 125 | 146 |
| 145 | 103 | 146 |
| 124 | 142 | 138 |
| 99 | 150 | 158 |
| 125 | 140 | 154 |
| 137 | 94 | 141 |
| 156 | 129 | 134 |
| 148 | 156 | 150 |
| 138 | 141 | 150 |
| 144 | 148 | 114 |
| 133 | 141 | 109 |
| 145 | 135 | 157 |
| 121 | 150 | 161 |
| 126 | 150 | 133 |
| 128 | 127 | 166 |
| 120 | 158 | 168 |
| 150 | 131 | 136 |
| 123 | 162 | 142 |
| 150 | 121 | 118 |
| 160 | 144 | 126 |
| 139 | 160 | 140 |
| 152 | 140 | 101 |
| 146 | 110 | 123 |
| 142 | 135 | 117 |
| 137 | 106 | 151 |
| 148 | 126 | 142 |
| 130 | 154 | 144 |
| 152 | 140 | 120 |
| 126 | 110 | 107 |
| 118 | 116 | 114 |
| 140 | 136 | 124 |
| 166 | 122 | 120 |
| 128 | 150 | 115 |
| 165 | 112 | |
| 143 | 124 | |
| 132 | 137 | |
| 130 | 130 | |
| 126 | 160 | |
| 166 | 150 | |
| 168 | ||
| 128 | ||
| 126 | ||
| 114 | ||
| 142 | ||
| 156 | ||
| 170 | ||
| 119 | ||
| 128 | ||
| 163 | ||
| 135 | ||
| 120 | ||
| 120 | ||
| 106 | ||
| 130 | ||
| 156 | ||
| 114 | ||
| 137 | ||
| 142 | ||
| 121 | ||
| 140 | ||
| 121 | ||
| 136 | ||
| 125 | ||
| 138 | ||
| 150 | ||
| 154 | ||
| 127 | ||
| 153 | ||
| 120 | ||
| 171 | ||
| 128 | ||
| 124 | ||
| 130 | ||
| 127 | ||
| 130 | ||
| 138 | ||
| 122 | ||
| 160 | ||
| 104 | ||
| 121 | ||
| 131 | ||
| 127 | ||
| 109 | ||
| 158 | ||
| 132 | ||
| 134 | ||
| 164 |
После вычислений получаем:
p =0.7913
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.1.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 136,7 | 2 | 68,326 |
| Остаточная | 51587,5 | 177 | 291,455 |
| Полная | 51724,2 | 179 | ----- |
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень гемоглобина в крови не зависит от стадии лечения.
Таблица 2.2.1. Зависимость СОЭ от стадии лечения
| 1 группа | 2 группа | 3 группа |
| 18 | 14 | 5 |
| 19 | 4 | 10 |
| 42 | 12 | 15 |
| 66 | 17 | 3 |
| 25 | 14 | 3 |
| 10 | 5 | 38 |
| 13 | 2 | 49 |
| 28 | 40 | 5 |
| 3 | 30 | 3 |
| 26 | 6 | 19 |
| 28 | 3 | 2 |
| 38 | 26 | 3 |
| 28 | 69 | 10 |
| 1 | 25 | 5 |
| 52 | 3 | 3 |
| 48 | 35 | 5 |
| 26 | 6 | 16 |
| 14 | 3 | 5 |
| 12 | 5 | 4 |
| 48 | 1 | 4 |
| 19 | 5 | 10 |
| 28 | 5 | 1 |
| 25 | 7 | 4 |
| 6 | 6 | 15 |
| 11 | 3 | 2 |
| 26 | 10 | 10 |
| 2 | 2 | 10 |
| 51 | 2 | 10 |
| 24 | 12 | 34 |
| 13 | 37 | 38 |
| 6 | 18 | 25 |
| 10 | 58 | 2 |
| 2 | 10 | 10 |
| 30 | 4 | 17 |
| 2 | 10 | 15 |
| 3 | 23 | 8 |
| 46 | 12 | 5 |
| 56 | 5 | 10 |
| 3 | 12 | 35 |
| 11 | 12 | 39 |
| 4 | 10 | |
| 4 | 30 | |
| 24 | 24 | |
| 11 | 40 | |
| 7 | 2 | |
| 1 | 2 | |
| 7 | ||
| 9 | ||
| 20 | ||
| 34 | ||
| 4 | ||
| 24 | ||
| 1 | ||
| 35 | ||
| 16 | ||
| 1 | ||
| 36 | ||
| 22 | ||
| 34 | ||
| 50 | ||
| 28 | ||
| 14 | ||
| 64 | ||
| 30 | ||
| 9 | ||
| 32 | ||
| 10 | ||
| 21 | ||
| 3 | ||
| 7 | ||
| 22 | ||
| 26 | ||
| 12 | ||
| 6 | ||
| 1 | ||
| 18 | ||
| 1 | ||
| 2 | ||
| 10 | ||
| 26 | ||
| 6 | ||
| 4 | ||
| 12 | ||
| 25 | ||
| 4 | ||
| 40 | ||
| 52 | ||
| 18 | ||
| 62 | ||
| 40 | ||
| 7 | ||
| 5 | ||
| 3 | ||
| 8 |
После вычислений получаем:
p = 0.0219
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.2.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 136,7 | 2 | 68,326 |
| Остаточная | 51587,5 | 177 | 291,455 |
| Полная | 51724,2 | 179 | ----- |
p<pкр
Вывод:
Следовательно мы отвергаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости СОЭ зависит от стадии лечения. Используя функцию multcompare, целесообразно определить для какой пары выборок средние арифметические значения имеют статистически значимое различие. Для проверки такой параметрической гипотезы используется процедура множественного сравнения. При проверке простой параметрической гипотезы (нулевой гипотезы) о равенстве средних одной группы выборок по отношению к другой по статистике t необходимо задать уровень значимости ![]() , определяющий критическое значение статистики
, определяющий критическое значение статистики![]() . Примем
. Примем![]() равным 0,05. Это означает, что в 5% случаев будет неверно отвергнута нулевая гипотеза.
равным 0,05. Это означает, что в 5% случаев будет неверно отвергнута нулевая гипотеза.
При увеличении групп выборок, увеличивается число проверяемых гипотез.
При использовании простой параметрической гипотезы по статистике t, уровень значимости ![]() будет применяться к каждой гипотезе отдельно, что повлечет к росту вероятности неверно отвергнуть нулевую гипотезу пропорционально количеству выполненных проверок. Т.е., неверно определить значимое отличие выборочных средних. Процедура множественного сравнения обеспечивает заданный уровень значимости для каждой проверки.
будет применяться к каждой гипотезе отдельно, что повлечет к росту вероятности неверно отвергнуть нулевую гипотезу пропорционально количеству выполненных проверок. Т.е., неверно определить значимое отличие выборочных средних. Процедура множественного сравнения обеспечивает заданный уровень значимости для каждой проверки.
Выходной параметр с представляет результаты множественного сравнения в виде матрицы из 5 столбцов. Срока матрицы с соответствуют результатам проверки одной параметрической гипотезы. Таким образом, каждая строка с соответствует одной паре выборок. Первые два значения в строке с показывают номера сравниваемых выборок, пятый - величину разности средних арифметических сравниваемых выборок, четвертый и третий столбцы - 95% доверительный интервал полученной разности средних арифметических.
Таблица 2.2.3 Различия между средними для СОЭ
| № группы | № группы | Нижняя граница доверительного интервала | Разница средних арифметических | Верхняя граница доверительного интервала |
| 1 группа | 2 группа | -1.2331 | 5.3127 | 11.8585 |
| 1 группа | 3 группа | 0.5745 | 7.4420 | 14.3096 |
| 2 группа | 3 группа | -5.7354 | 2.1293 | 9.9941 |
Полученные значения показывают, что значимая разница средних арифметических наблюдается между 1 и 3 группой, величина их разности равна 7.4420, 95% доверительный интервал полученной разности средних арифметических составил [0,5745, 14.3096]. Различия считаются значимыми, если в доверительный интервал не попало нулевое значение. Т.е. средние арифметические выборок статистически значимо отличаются друг от друга, для ![]() .
.
Отобразим графически значения средних арифметических и их доверительных интервалов. Два выборочных средних значимо отличаются, если их доверительные интервалы не пересекаются на графике. При наложении границ доверительных интервалов двух средних арифметических, различие между ними можно считать статистически незначимым.
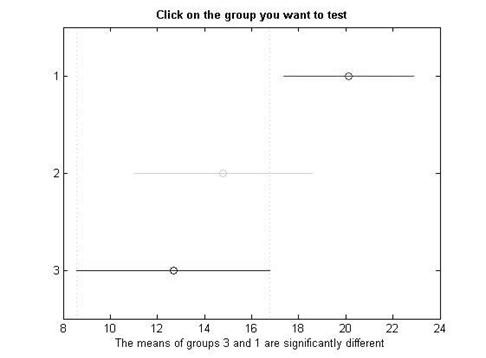
Таблица 2.3.1. Зависимость СРБ от стадии лечения
| 1 группа | 2 группа | 3 группа |
| 0 | 0 | 0 |
| 6 | 0 | 0 |
| 96 | 0 | 0 |
| 192 | 0 | 0 |
| 0 | 6 | 0 |
| 0 | 0 | 96 |
| 0 | 0 | 48 |
| 0 | 192 | 0 |
| 0 | 48 | 0 |
| 0 | 0 | 48 |
| 48 | 0 | 0 |
| 0 | 192 | 0 |
| 12 | 768 | 6 |
| 0 | 6 | 0 |
| 384 | 0 | 0 |
| 192 | 96 | 0 |
| 12 | 24 | 0 |
| 48 | 6 | 0 |
| 0 | 0 | 0 |
| 96 | 0 | 0 |
| 0 | 0 | 0 |
| 48 | 0 | 0 |
| 0 | 0 | 0 |
| 12 | 0 | 0 |
| 6 | 0 | 0 |
| 6 | 0 | 0 |
| 0 | 0 | 0 |
| 96 | 0 | 0 |
| 48 | 0 | 12 |
| 6 | 0 | 96 |
| 0 | 0 | 0 |
| 0 | 48 | 0 |
| 0 | 0 | 0 |
| 0 | 0 | 48 |
| 0 | 0 | 0 |
| 0 | 12 | 0 |
| 768 | 0 | 0 |
| 96 | 0 | 0 |
| 0 | 0 | 48 |
| 0 | 0 | 48 |
| 0 | 0 | |
| 0 | 96 | |
| 0 | 96 | |
| 12 | 48 | |
| 0 | 0 | |
| 0 | 0 | |
| 6 | ||
| 0 | ||
| 6 | ||
| 6 | ||
| 0 | ||
| 48 | ||
| 0 | ||
| 6 | ||
| 6 | ||
| 0 | ||
| 12 | ||
| 0 | ||
| 0 | ||
| 192 | ||
| 0 | ||
| 6 | ||
| 48 | ||
| 6 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 12 | ||
| 12 | ||
| 6 | ||
| 0 | ||
| 0 | ||
| 48 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 96 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 48 | ||
| 0 | ||
| 384 | ||
| 48 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 |
После вычислений:
p = 0.4019
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.3.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 16791,5 | 2 | 8395,73 |
| Остаточная | 1621687,7 | 177 | 9162,08 |
| Полная | 1638479,2 | 179 | ----- |
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень СРБ в крови не зависит от стадии лечения.
Таблица 2.4.1. Зависимость фибриногена от стадии лечения
| 1 группа | 2 группа | 3 группа |
| 3,00 | 4,00 | 3,75 |
| 4,50 | 4,00 | 4,00 |
| 3,50 | 3,00 | 3,00 |
| 7,25 | 4,00 | 2,75 |
| 4,00 | 3,00 | 2,00 |
| 3,25 | 3,20 | 6,00 |
| 5,50 | 2,00 | 3,50 |
| 4,00 | 8,75 | 3,00 |
| 3,25 | 4,00 | 2,50 |
| 5,00 | 4,00 | 4,75 |
| 3,60 | 5,00 | 3,00 |
| 4,25 | 5,00 | 2,75 |
| 4,25 | 7,50 | 3,25 |
| 3,00 | 4,00 | 2,50 |
| 10,20 | 3,25 | 2,00 |
| 4,75 | 2,90 | 3,10 |
| 4,50 | 3,25 | 2,00 |
| 5,00 | 2,90 | 3,25 |
| 5,50 | 3,00 | 3,25 |
| 5,50 | 2,00 | 3,00 |
| 3,75 | 3,00 | 3,25 |
| 3,75 | 2,00 | 3,25 |
| 4,50 | 3,00 | 4,00 |
| 5,75 | 2,93 | 3,00 |
| 3,00 | 4,25 | 2,00 |
| 4,25 | 3,25 | 3,25 |
| 3,75 | 2,50 | 2,50 |
| 5,25 | 3,00 | 3,25 |
| 6,25 | 3,50 | 4,30 |
| 2,25 | 5,00 | 4,25 |
| 3,25 | 3,30 | 4,00 |
| 2,50 | 5,00 | 2,25 |
| 2,75 | 4,25 | 2,10 |
| 4,00 | 2,00 | 4,75 |
| 2,75 | 3,25 | 3,50 |
| 4,00 | 4,25 | 3,00 |
| 4,50 | 3,50 | 2,00 |
| 6,75 | 3,00 | 1,75 |
| 3,25 | 2,00 | 4,25 |
| 3,75 | 3,50 | 3,00 |
| 3,25 | 4,00 | |
| 4,00 | 3,50 | |
| 4,25 | 3,00 | |
| 3,50 | 2,75 | |
| 2,60 | 3,00 | |
| 2,75 | 2,75 | |
| 4,25 | ||
| 2,00 | ||
| 3,75 | ||
| 5,25 | ||
| 2,00 | ||
| 5,75 | ||
| 2,50 | ||
| 5,50 | ||
| 3,50 | ||
| 3,25 | ||
| 7,25 | ||
| 3,75 | ||
| 3,00 | ||
| 7,00 | ||
| 5,50 | ||
| 4,00 | ||
| 7,50 | ||
| 3,50 | ||
| 4,00 | ||
| 5,50 | ||
| 6,75 | ||
| 2,50 | ||
| 3,10 | ||
| 3,00 | ||
| 6,75 | ||
| 4,50 | ||
| 3,50 | ||
| 2,50 | ||
| 2,50 | ||
| 4,50 | ||
| 3,00 | ||
| 2,15 | ||
| 2,80 | ||
| 3,75 | ||
| 2,50 | ||
| 3,00 | ||
| 3,25 | ||
| 3,50 | ||
| 3,75 | ||
| 5,25 | ||
| 5,10 | ||
| 4,50 | ||
| 12,20 | ||
| 5,75 | ||
| 5,50 | ||
| 3,00 | ||
| 2,50 | ||
| 3,00 |
p = 0.0003
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.4.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 34,806 | 2 | 17,4029 |
| Остаточная | 365,662 | 177 | 2,0659 |
| Полная | 400,467 | 179 | ----- |
p<pкр
Вывод:
Следовательно мы отвергаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости фибриноген зависит от стадии лечения. Используя функцию multcompare, целесообразно определить для какой пары выборок средние арифметические значения имеют статистически значимое различие.
Таблица 2.4.3 Различия между средними для фибриногена
| № группы | № группы | Нижняя граница доверительно интервала | Разница средних арифметических | Верхняя граница доверительного интервала |
| 1 группа | 2 группа | -0.1003 | 0.6532 | 1.4067 |
| 1 группа | 3 группа | 0.2579 | 1.0484 | 1.8389 |
| 2 группа | 3 группа | -0.5101 | 0.3952 | 1.3005 |
Полученные значения показывают, что значимая разница средних арифметических наблюдается между 1 и 3 группой, величина их разности равна 1.0484, 95% доверительный интервал полученной разности средних арифметических составил [0,2579, 1.8389]. Т.е. средние арифметические выборок статистически значимо отличаются друг от друга, для ![]() .
.
Отобразим графически значения средних арифметических и их доверительных интервалов.
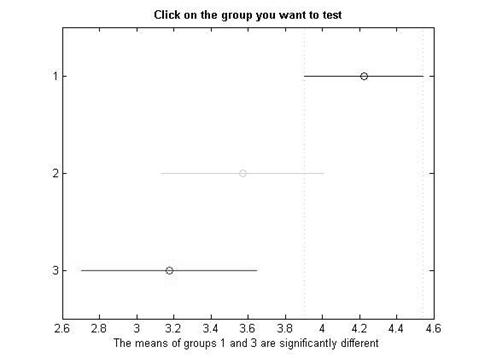
Таблица 2.5.1. Зависимость ВАШБП от стадии лечения
| 1 группа | 2 группа | 3 группа |
| 15 | 36 | 5 |
| 28 | 20 | 38 |
| 63 | 38 | 5 |
| 45 | 15 | 0 |
| 40 | 53 | 5 |
| 80 | 12 | 65 |
| 20 | 23 | 57 |
| 48 | 40 | 5 |
| 75 | 52 | 0 |
| 35 | 25 | 25 |
| 55 | 0 | 5 |
| 85 | 70 | 20 |
| 45 | 95 | 21 |
| 43 | 25 | 5 |
| 45 | 10 | 10 |
| 50 | 27 | 15 |
| 50 | 40 | 15 |
| 56 | 45 | 23 |
| 10 | 15 | 35 |
| 55 | 17 | 3 |
| 45 | 25 | 10 |
| 95 | 25 | 37 |
| 32 | 10 | 7 |
| 25 | 35 | 10 |
| 70 | 12 | 5 |
| 45 | 28 | 25 |
| 28 | 15 | 10 |
| 27 | 25 | 2 |
| 75 | 17 | 35 |
| 45 | 70 | 60 |
| 55 | 45 | 45 |
| 35 | 55 | 20 |
| 33 | 40 | 13 |
| 5 | 25 | 30 |
| 45 | 20 | 5 |
| 35 | 40 | 55 |
| 73 | 75 | 30 |
| 55 | 30 | 25 |
| 56 | 55 | 16 |
| 43 | 15 | 30 |
| 55 | 30 | |
| 20 | 20 | |
| 53 | 40 | |
| 30 | 35 | |
| 55 | 35 | |
| 55 | 15 | |
| 15 | ||
| 70 | ||
| 60 | ||
| 25 | ||
| 25 | ||
| 35 | ||
| 33 | ||
| 65 | ||
| 45 | ||
| 50 | ||
| 25 | ||
| 45 | ||
| 44 | ||
| 100 | ||
| 65 | ||
| 55 | ||
| 64 | ||
| 15 | ||
| 15 | ||
| 40 | ||
| 45 | ||
| 57 | ||
| 40 | ||
| 33 | ||
| 55 | ||
| 50 | ||
| 55 | ||
| 40 | ||
| 0 | ||
| 45 | ||
| 48 | ||
| 30 | ||
| 67 | ||
| 65 | ||
| 50 | ||
| 45 | ||
| 55 | ||
| 27 | ||
| 58 | ||
| 45 | ||
| 30 | ||
| 50 | ||
| 35 | ||
| 20 | ||
| 78 | ||
| 50 | ||
| 60 | ||
| 75 |
После вычислений получаем:
p = 4.8659e-011
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.5.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 19350,2 | 2 | 9675,1 |
| Остаточная | 62873,6 | 177 | 355,22 |
| Полная | 82223,8 | 179 | ----- |
p<pкр
Вывод:
Следовательно мы отвергаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости ВАШБП зависит от стадии лечения. Используя функцию multcompare, целесообразно определить для какой пары выборок средние арифметические значения имеют статистически значимое различие.
Таблица 2.5.3 Различия между средними для ВАШБП
| № группы | № группы | Нижняя граница доверительно интервала | Разница средних арифметических | Верхняя граница доверительного интервала |
| 1 группа | 2 группа | 3,7045 | 13,5851 | 23,4657 |
| 1 группа | 3 группа | 15,0439 | 25,4101 | 35,7763 |
| 2 группа | 3 группа | -0.0464 | 11,8250 | 23,6964 |
Полученные значения показывают, что значимая разница средних арифметических наблюдается между 1 и 2 группой и 1 и 3 группой.
Отобразим графически значения средних арифметических и их доверительных интервалов.
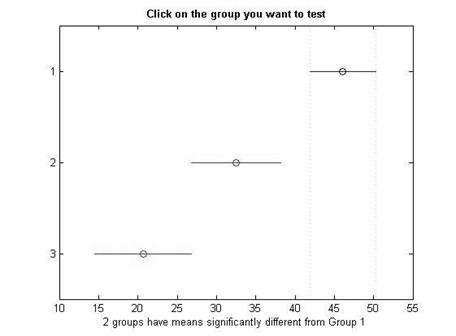
Таблица 2.6.1. Зависимость ВАШСП от стадии лечения
| 1 группа | 2 группа | 3 группа |
| 20 | 41 | 10 |
| 53 | 30 | 50 |
| 68 | 43 | 3 |
| 55 | 17 | 0 |
| 43 | 60 | 5 |
| 75 | 15 | 63 |
| 12 | 20 | 58 |
| 40 | 41 | 10 |
| 67 | 43 | 0 |
| 38 | 40 | 80 |
| 80 | 5 | 10 |
| 80 | 80 | 30 |
| 41 | 95 | 20 |
| 65 | 35 | 5 |
| 50 | 20 | 9 |
| 48 | 35 | 10 |
| 45 | 40 | 40 |
| 50 | 48 | 20 |
| 25 | 18 | 33 |
| 40 | 18 | 5 |
| 55 | 40 | 18 |
| 89 | 60 | 40 |
| 60 | 10 | 15 |
| 25 | 20 | 10 |
| 70 | 12 | 20 |
| 50 | 28 | 35 |
| 50 | 30 | 20 |
| 55 | 35 | 2 |
| 55 | 29 | 37 |
| 60 | 68 | 55 |
| 55 | 45 | 50 |
| 40 | 70 | 25 |
| 32 | 50 | 20 |
| 40 | 34 | 39 |
| 54 | 30 | 10 |
| 47 | 32 | 50 |
| 80 | 75 | 20 |
| 78 | 30 | 20 |
| 65 | 19 | 50 |
| 50 | 10 | 40 |
| 62 | 31 | |
| 25 | 60 | |
| 52 | 45 | |
| 50 | 45 | |
| 30 | 39 | |
| 60 | 15 | |
| 19 | ||
| 70 | ||
| 70 | ||
| 35 | ||
| 32 | ||
| 28 | ||
| 40 | ||
| 65 | ||
| 25 | ||
| 70 | ||
| 38 | ||
| 52 | ||
| 40 | ||
| 100 | ||
| 55 | ||
| 50 | ||
| 78 | ||
| 15 | ||
| 38 | ||
| 50 | ||
| 62 | ||
| 70 | ||
| 40 | ||
| 50 | ||
| 60 | ||
| 56 | ||
| 68 | ||
| 20 | ||
| 10 | ||
| 40 | ||
| 70 | ||
| 50 | ||
| 70 | ||
| 78 | ||
| 41 | ||
| 30 | ||
| 60 | ||
| 40 | ||
| 60 | ||
| 42 | ||
| 83 | ||
| 53 | ||
| 70 | ||
| 51 | ||
| 70 | ||
| 80 | ||
| 70 | ||
| 80 |
После вычислений получаем:
p =1.0573e-011
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.6.2. Дисперсионный анализ по одному признаку.
| Компонента дисперсии | Сумма квадратов | Степень свободы | Средний квадрат |
| Между выборками | 21595,1 | 2 | 10797,6 |
| Остаточная | 65337,4 | 177 | 369,1 |
| Полная | 86932,6 | 179 | ----- |
p<pкр
Вывод:
Следовательно мы отвергаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости ВАШСП зависит от стадии лечения. Используя функцию multcompare, целесообразно определить для какой пары выборок средние арифметические значения имеют статистически значимое различие.
Таблица 2.6.3 Различия между средними для ВАШСП
| № группы | № группы | Нижняя граница доверительно интервала | Разница средних арифметических | Верхняя граница доверительного интервала |
| 1 группа | 2 группа | 5,2663 | 15,3386 | 25,4109 |
| 1 группа | 3 группа | 15,9332 | 26,5005 | 37,0679 |
| 2 группа | 3 группа | -0.9398 | 11,1620 | 23,2637 |
Полученные значения показывают, что значимая разница средних арифметических наблюдается между 1 и 2 группой и 1 и 3 группой.
Отобразим графически значения средних арифметических и их доверительных интервалов.
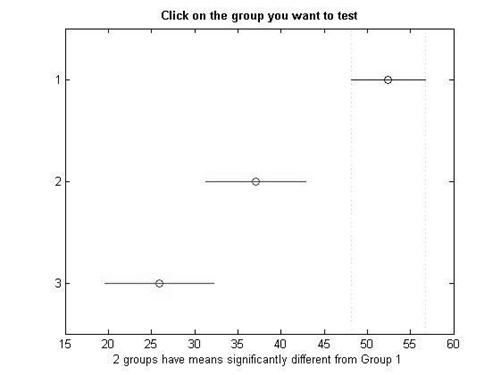

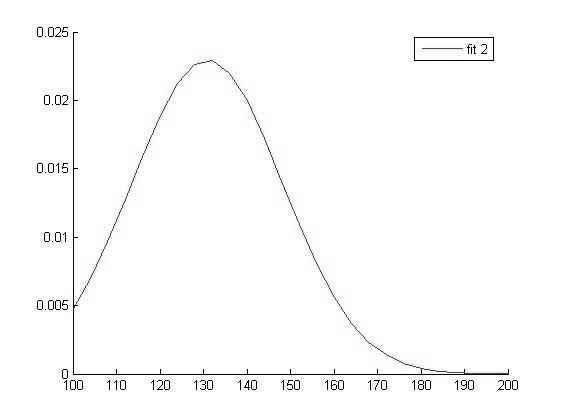
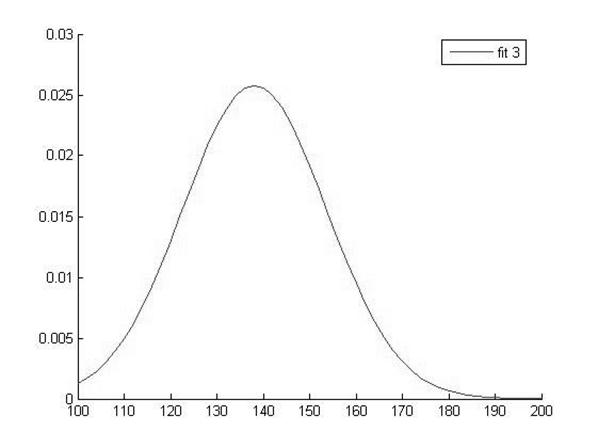
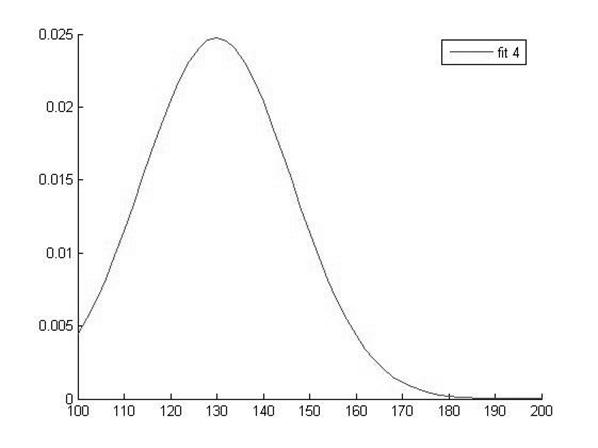
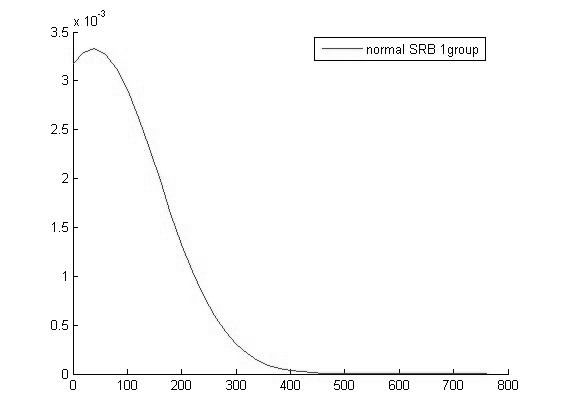
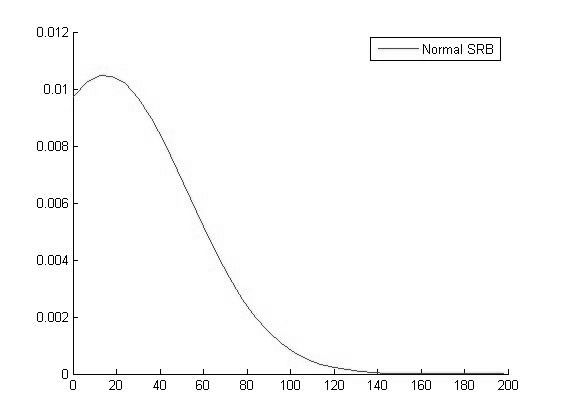
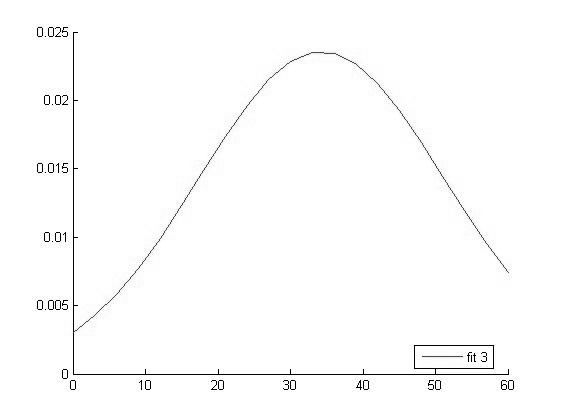
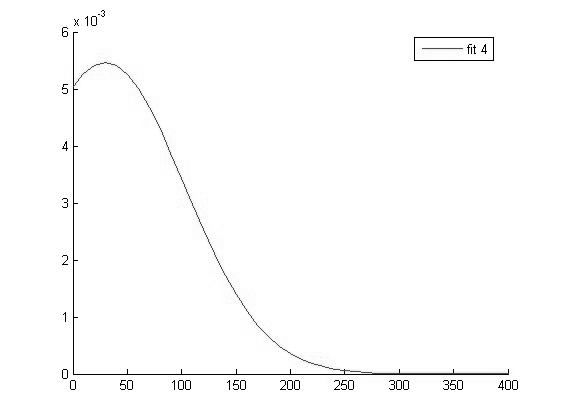
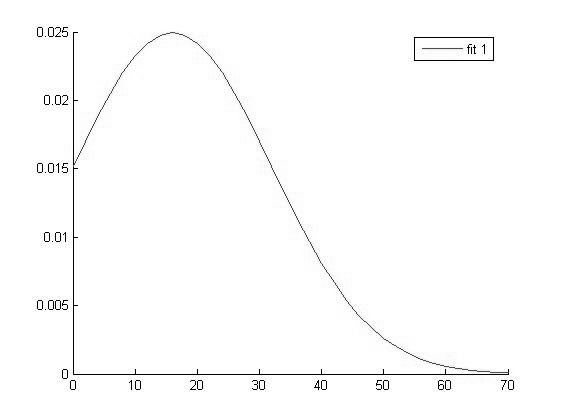
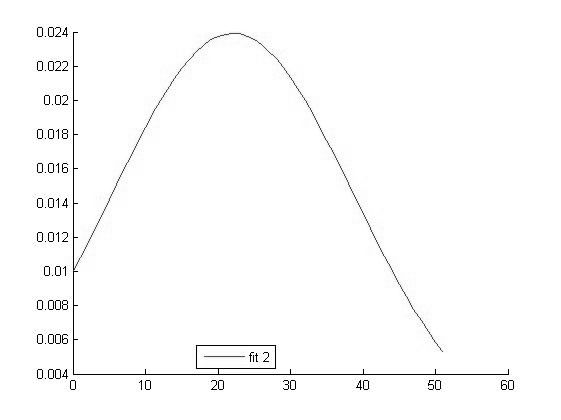
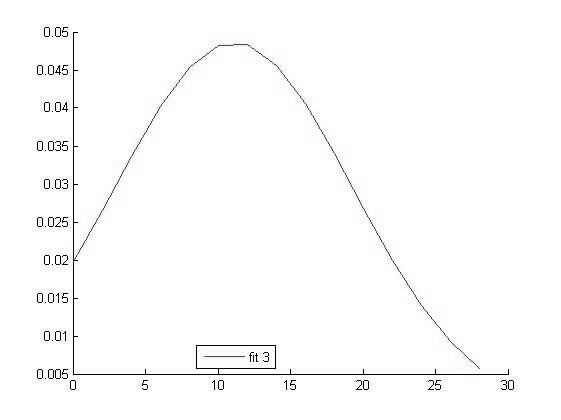
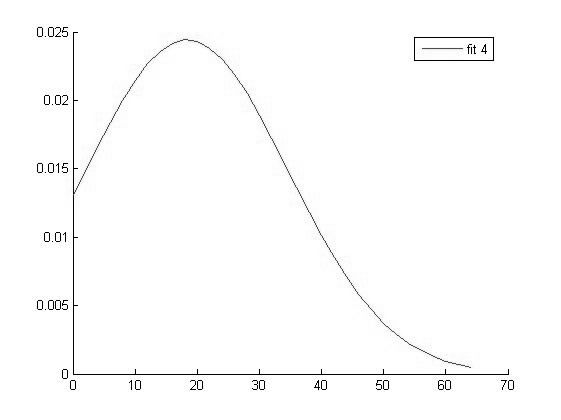
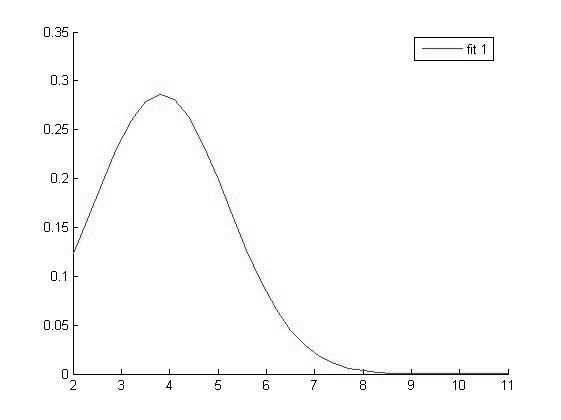
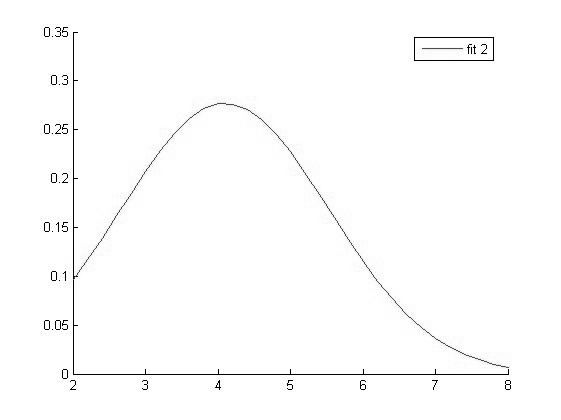
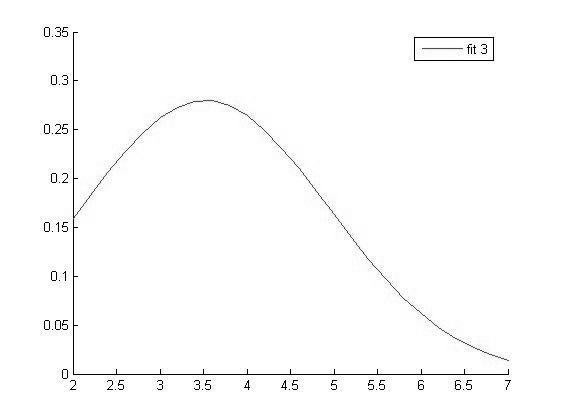
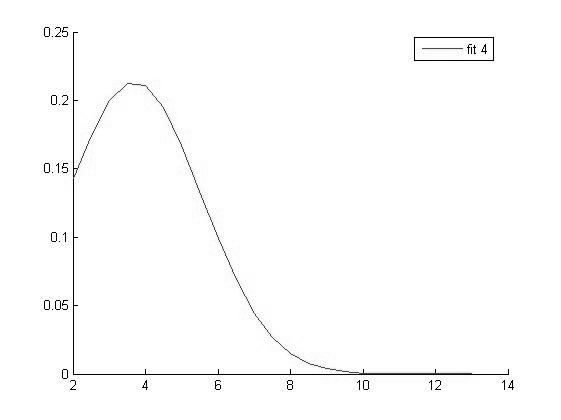
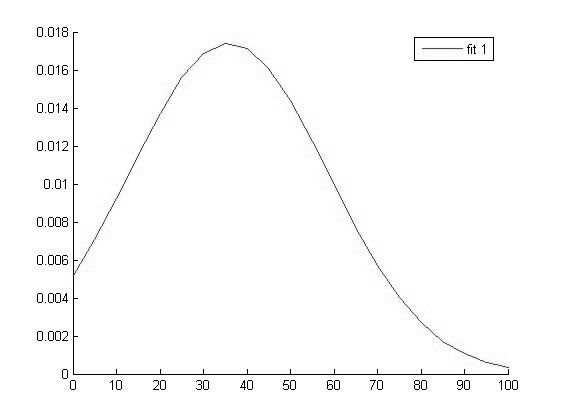
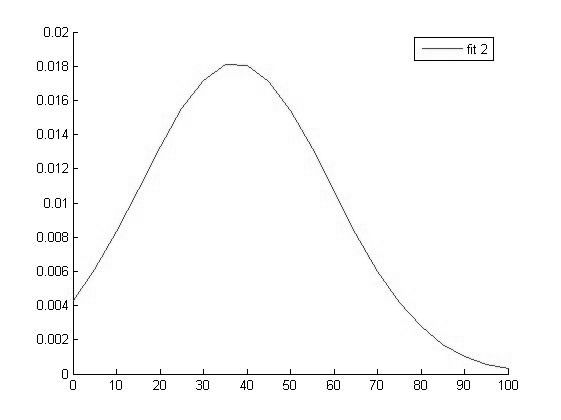
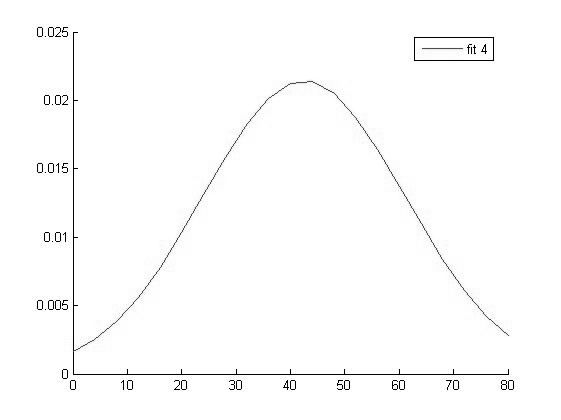
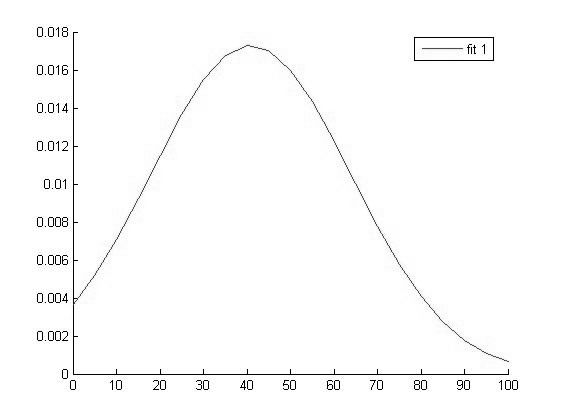
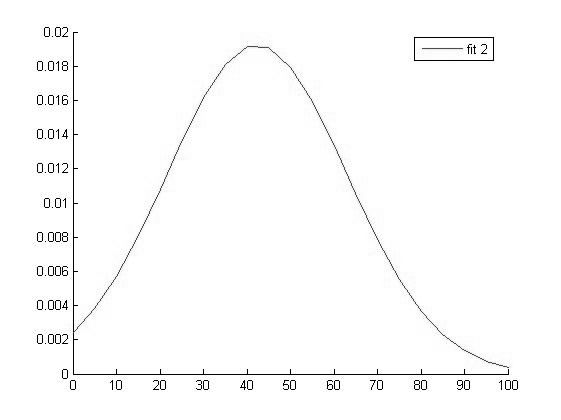
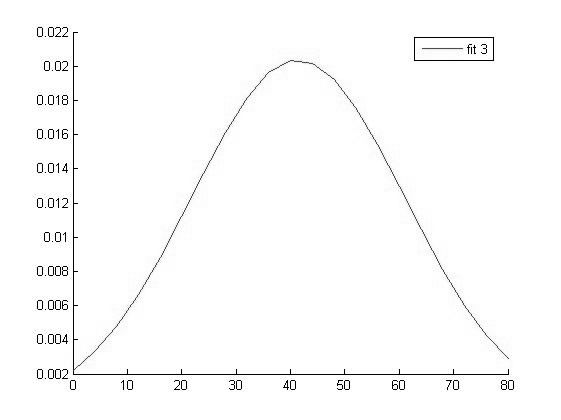
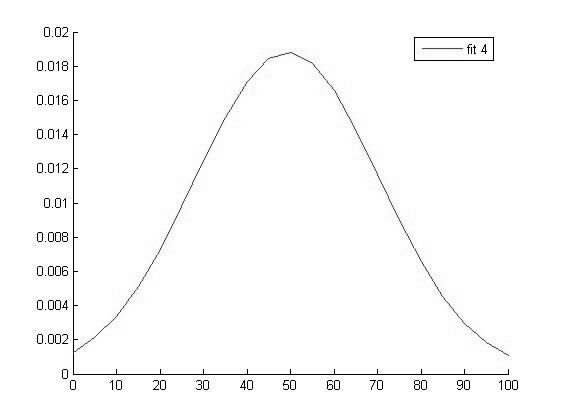
0 комментариев