Навигация
Изменение коэффициента ЦФ базисной переменной всегда приводит к изменению значения ЦФ
2. Изменение коэффициента ЦФ базисной переменной всегда приводит к изменению значения ЦФ.
3. Эффект от изменения коэффициентов ЦФ может рассматриваться с двух позиций :
- с точки зрения сбыта нас интересуют равновесные цены;
- с точки зрения производства нас интересует диапазон изменения коэффициента ЦФ, ' в пределах которого текущий план производства остается оптимальным.
Нахождение диапазонов изменения запасов ресурсов
Недефицитные ресурсы
Если в оптимальном решении дополнительная переменная S i-ro ограничения базисная, то это ограничение является не связывающим (не активным в точке оптимума), а ресурс - недефицитный. В этом случае значение дополнительной базисной переменной дает диапазон изменения, в котором соответствующая компонента di может:
• Уменьшатся (в случае знака ограничения "<")
• Увеличивается (в случае знака ограничения ">").
Пусть S0 - значение соответствующей дополнительной переменной в точке оптимума. Тогда решение остаётся допустимым и оптимальным в диапазоне bi+ ∆ , где
Дефицитные ресурсы
Если в оптимальном решении некоторая дополнительная переменная небазисная, то существующее ' ей ограничение является связывающим (активным в точке оптимума), а ресурс - дефицитным.
Для ограничения типа "<":
Для ограничения типа ">":
Изменение коэффициентов Ц.Ф.
Существует диапазон изменения коэффициентов ' целевой функции как базисных так и не базисных переменных, в которых полученное решение остаётся оптимальным. Изменение коэффициента базисной переменной в пределах этого диапазона приводит к изменению значения целевой функции, так как Z = Ств*β, а одна из компонент вектора Св изменяется. Изменение коэффициента небазисной переменной не меняет значения задачи.
Для задачи на mах:
Базисные переменные:
Для базисной переменной диапазон устойчивости, в котором может изменяться коэффициент Ci , оставляя текущее решение оптимальным, задаётся выражением: Ci + ∆
где dj - относительная оценка переменной xj в текущем оптимальном решении.
Eсли отсутствуют ![]() соответственно.
соответственно.
Не базисные переменные:
Для не базисной переменной диапазон устойчивости, в котором может изменятся коэффициент Сi оставляя текущее решение оптимальным, задаётся выражением:
Для задачи на min: Базисные переменные:
Для базисной переменной диапазон устойчивости, в котором может изменяться коэффициент Сi , оставляя текущее решение оптимальным, задаётся выражением: Сi + ∆
He базисные переменные:
Для не базисной переменной диапазон устойчивости, в котором может изменятся коэффициент С; оставляя текущее решение оптимальным, задаётся выражением:
(dN) < ∆ < ∞
2. Содержательная постановка задачи
Вариант 3/2
Транспортная компания для перевозки инжира из Багдада в Мекку использует мулов, одногорбых и двугорбых верблюдов. Двугорбый верблюд может перевезти - 1000 фунтов, одногорбый – 500 фунтов, а мул – 300 фунтов. За один переход двугорбый верблюд потребляет 2 кипы сена и 40 галлонов воды. Одногорбый верблюд потребляет 2 кипы сена и 30 галлонов воды. Мул – 1 кипу сена и 10 галлонов воды. Пункты снабжения компании, расположенные в различных оазисах вдоль пути, могут выдать не более 900 галлонов воды и 35 кип сена. Верблюды и мулы арендуются у пастуха близ Багдада, арендная плата равна 12 пиастрам за двугорбого верблюда, 5 пиастрам за одногорбого и 4 пиастрам за мула.
Если компания должна перевести 8000 фунтов инжира из Багдада в Мекку, сколько надо использовать верблюдов и мулов для минимизации арендной платы пастуху?
3. Математическая постановка задачи
Переменные:
Х1 - Двугорбый верблюд
Х2 - Одногорбый верблюд
Х3 – Мул
Целевая функция – минимизация арендной платы.
Zmin = 12Х1 + 5Х2+ 4Х3
Ограничения:
Использования ресурса «вода» не более 900 галлонов:
40Х1 + 30Х2+ 10Х3 < 900
Использования ресурса «сено» не более 35 кип:
3Х1 + 2Х2+ Х3 < 35
Компания должна перевести 8000 фунтов инжира:
1000Х1 + 500Х2 + 300Х3 =8000
Все переменные должны быть не отрицательны:
Х1, Х2, Х3 > 0
4. Решения задачи симплекс-методом
ЦФ:
Zmin = 12X1 + 5X2 + 4X3
Ограничения:
![]() 40X1 + 30X2 + 10X3 < 900
40X1 + 30X2 + 10X3 < 900
3X1 + 2X2 + X3 < 35
1000X1 + 500X2 + 300X3 = 8000
X1, X2, X3 > 0
Приведем задачу к канонической форме и введём искусственные переменные:
![]() Zmin = 12X1 + 5X2 + 4X3 + 0S1 + 0S2 – MR1
Zmin = 12X1 + 5X2 + 4X3 + 0S1 + 0S2 – MR1
40X1 + 30X2 + 10X3 + 0S1 = 900
3X1 + 2X2 + X3 + 0S2 = 35
1000X1 + 500X2 + 300X3 + R1 = 8000
X1, X2, X3 > 0
R1 = – 1000X1 – 500X2 – 300X3 + 8000
Zmin = 12X1 + 5X2 + 4X3 + 0S1 + 0S2 – M (– 1000X1 – 500X2 – 300X3 + 8000) = (12 + 1000M) X1 + (5 + 500M) X2 + (4 + 300M) X3 – 8000M
Z + (–12 – 1000M) X1 + (–5 – 500M) X2 + (–4 – 300M) X3 = – 8000M
Составляем симплекс таблицу:
| Шаг 0 | |||||||
| БП | X 1 | X2 | X3 | S1 | S2 | R1 | решение |
| S1 | 40 | 30 | 10 | 1 | 0 | 0 | 900 |
| S2 | 3 | 2 | 1 | 0 | 1 | 0 | 35 |
| R1 | 1000 | 500 | 300 | 0 | 0 | 1 | 8000 |
| Z | -1000M+12 | -500M+5 | -300M+4 | 0 | 0 | 0 | -8000M |
| Шаг 1 | |||||||
| S1 | 0 | 10 | -2 | 1 | 0 | -1/25 | 580 |
| S2 | 0 | 1/2 | 1/10 | 0 | 1 | -3/1000 | 11 |
| X1 | 1 | 1/2 | 3/10 | 0 | 0 | 1/1000 | 8 |
| Z | 0 | -1 | 2/5 | 0 | 0 | M-3/250 | -96 |
| Шаг 2 | |||||||
| S1 | -20 | 0 | -8 | 1 | 0 | -3/50 | 420 |
| S2 | -1 | 0 | -1/5 | 0 | 1 | -1/250 | 3 |
| X2 | 2 | 1 | 3/5 | 0 | 0 | 1/500 | 16 |
| Z | 2 | 0 | 1 | 0 | 0 | M-1/100 | -80 |
В итоге: Z = 80, X1 = 0, X2 = 16, X3 = 0
Похожие работы
... приведено значение целевой функции до начала вычислений, в столбце Результат - после оптимизации. Следующая таблица содержит значения искомых переменных (изменяемых ячеек) до и после решения задачи. оптимизация математическая электронная модель Последняя таблица показывает значения левых частей ограничений на оптимальном решении задачи. В столбце Формула приведены зависимости, которые были ...
... ряд соображений, которые этим расчетом не были учтены. В зависимости от того, какой информацией обладают руководитель и его сотрудники, подготавливающие решения, меняются и условия принятия решений и математические методы, применяемые для выработки рекомендаций. Если известны все действующие в системе факторы, то есть отстствуют случайные воздействия, то это будет принятие решений в ...
... 2 и 3. Трудоемкость товара 1 вдвое больше чем товара 2 и втрое больше чем товара 3 По условию задачи сказано, что минимальный спрос на продукцию завода составляет 50, 50 и 30 изделий моделей 1, 2 и 3 соответственно: Запишем все в математическую модель задачи: 2. Решим данную задачу симплекс методом Перепишем условие мат. Модели таким образом, чтоб все ограничения задачи имели ...
... , которая способствует обеспечению перехода от «производства вещей» к «производству людей», что адекватно новому видению значимости человека в современном мире и общественном производстве. 2.3 Причины и факторы стремительного развития сферы услуг В современных публикациях можно встретить более или менее развернутый перечень причин стремительного развития сферы услуг, различных по значению и ...
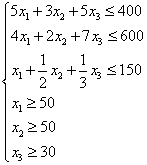
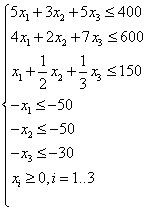
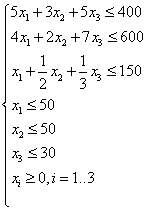
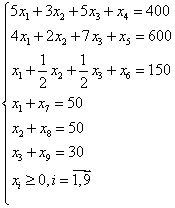
0 комментариев