Умножение
Умножение матриц (Произведение матриц):
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Это условие не выполняется, произведение АВ не существует.
Произведение матрицы и вектора Аb:
![]()
Скалярное произведение векторов (b,с):
![]()
Найти определитель матрицы А:
В частности, формула вычисления определителя матрицы ![]() такова:
такова:
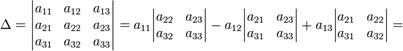
= a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31
=2*(-4)*5 – 2*4*2 – (-2)*5*5 + (-2)*4*(-1) +(-1)*5*2 – (-1)*(-4)*(-1) = -40 – 16 +50 + 8 – 10 + 4 = -4
Найти обратную матрицу А-1:
Решение.

Определитель введенной Вами матрицы равен:
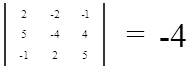
Определитель не равен нулю, следовательно обратная матрица существует.
Допишем к исходной матрице единичную матрицу справа.
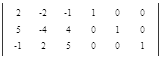
Начнем приведение левой квадратной матрицы к единичному виду. При помощи элементарных преобразований уберем все коэффициенты ниже главной диагонали.
Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
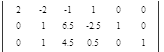
Вычтем 2 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.

Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1.
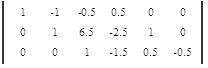
Приведем все коэффициенты выше главной диагонали к 0, при помощи элементарных преобразований.
Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.

Вычтем 2 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.

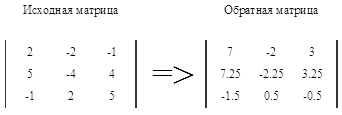
Ответ.
Как уже ранее упоминалось, мы при помощи элементарных преобразований переместили единичную матрицу из правой части в левую, при этом не нарушив ни одного правила работы с матрица.
Квадратная матрица, которую Вы видите справа и есть обратная матрица к введенной Вами.
Решение системы уравнений Ах=b:
Условие

Решение
Найдем определитель главной матрицы, составленной из коэффициентов при X1 - n:
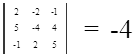
Определитель главной матрицы системы уравнений не равен нулю, следовательно данная система уравнений имеет единственное решение. Найдем его. Достоим главный определитель системы уравнений еще одним столбцом, в который вставим значения за знаком равенства.
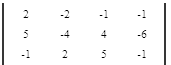
Теперь последовательно, при помощи элементарных преобразований преобразуем левую часть матрицы (3 × 3) до треугольного вида (обнулим все коэффициенты находящиеся не на главной диагонали, а коэффициенты на главной диагонали преобразуем до единиц).
Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.

Вычтем 2 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
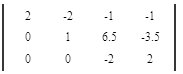
Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.

Вычтем 2 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
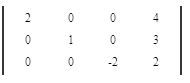
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1.
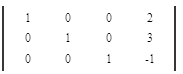
Ответ.
Числа получившиеся правее единичной матрицы и будут решением Вашей системы уравнений.

Элементарные преобразования матрицы
Элементарными преобразованиями матрицы называются следующие преобразования: 1) умножение строки матрицы на число, отличное от нуля; 2) прибавление к одной строке матрицы другой строки; 3) перестановка строк; 4) вычеркивание (удаление) одной из одинаковых строк (столбцов); 5) транспонирование матрицы;
Те же операции, применяемые для столбцов матрицы, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу матрицы прибавить линейную комбинацию остальных строк (столбцов).
Начинаем решать вот такую систему уравнений методом Гаусса

Определитель основной матрицы равен -4
Хотим сделать элемент [1,1] равным 1. Разделили всю строку 1 на элемент [1,1]=2.
![]()
Сделали в 1 строке элемент 1 единичным.
Обнулим 1 столбец: Из 2 строки вычли 1 строку, умноженную на элемент [1,2]=5.
![]()
Из 3 строки вычли 1 строку, умноженную на элемент [1,3]=-1.
![]()
Преобразование 1 столбца сделали.
Хотим сделать элемент [2,2] равным 1. Разделили всю строку 2 на элемент [2,2]=1.
![]()
Сделали в 2 строке элемент 2 единичным.
Обнулим 2 столбец: Из 1 строки вычли 2 строку, умноженную на элемент [2,1]=-1.
![]()
Из 3 строки вычли 2 строку, умноженную на элемент [2,3]=1.

Преобразование 2 столбца сделали.
Хотим сделать элемент [3,3] равным 1. Разделили всю строку 3 на элемент [3,3]=-2.

Сделали в 3 строке элемент 3 единичным.
Из 1 строки вычли 3 строку, умноженную на элемент [3,1]=6.

Из 2 строки вычли 3 строку, умноженную на элемент [3,2]=6.5.

Преобразование 3 столбца сделали.
Ну вот вроде и все. Решение содержится в правом столбце: ![]() Быстренько сделаем проверку: Исходная матрица:
Быстренько сделаем проверку: Исходная матрица:
![]()
Подставим в исходную матрицу полученные решения: в квадратных скобках элементы матрицы, в круглых решения системы уравнений
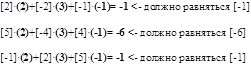
Похожие работы
... i < NumFE; i++) for (DWORD j = 0; j < 10; j++) FE[i][j]--; printf(" r"); return true;}ПРИЛОЖЕНИЕ 2. Исходный текст программы, реализующей алгоритм компактного хранения и решения СЛАУ высокого порядка. #include "matrix.h" class RVector { private: Vector<double> Buffer; public: RVector(void) {} ~RVector() {} RVector(DWORD Size) { Buffer. ...
... "деление" для матриц не вводится. Для квадратных невырожденных матриц вводится обратная матрица. С понятием обратной матрицы можно познакомиться в рекомендуемой литературе. 2 – ой учебный вопрос РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных ...
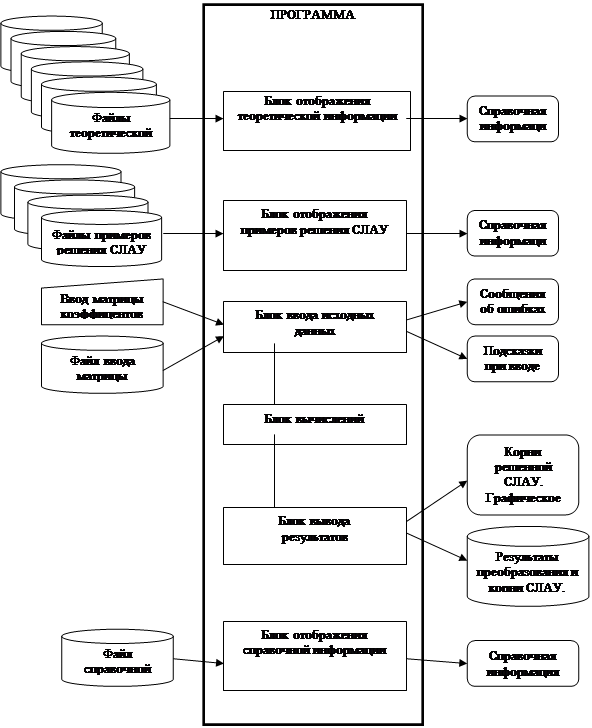
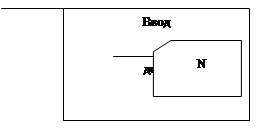
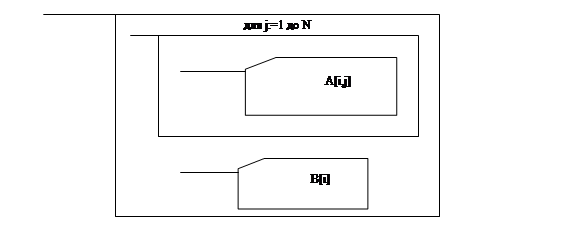
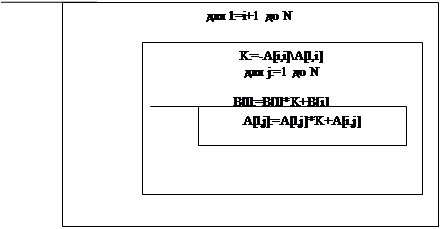
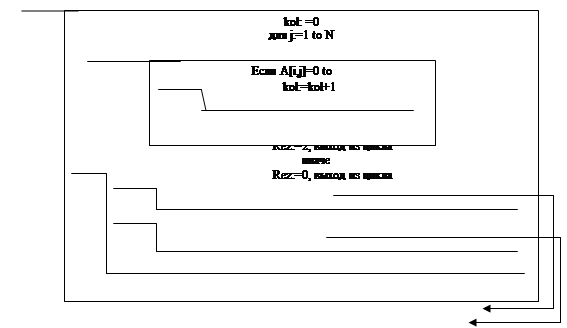
... Рисунок 1.1 - Схема информационных потоков для вычисления СЛАУ методом Гаусса Условные обозначения к рисунку 2.1: - данные, вводимые с клавиатуры - данные, хранящиеся на диске - данные, выводимые на экран 2. Решение систем линейных алгебраических уравнений методом гаусса 2.1 Основные понятия Система линейных алгебраических уравнений (СЛАУ) из m уравнений с n неизвестными ...
... V Бизнес с неблагоприятными перспективами, в котором компания имеет значительную рыночную долю. Пример: алкилатные моющие средства. Табл. 4 представляет классификацию секторов бизнеса табл. 1 в порядке приоритетов их ресурсного обеспечения. Необходимо отметить, что новые предприятия или направления бизнеса типа «удвоить активность» или «уйти с рынка» привлекают внимание только после секторов ...
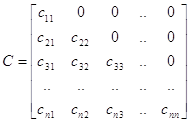

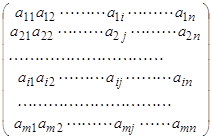
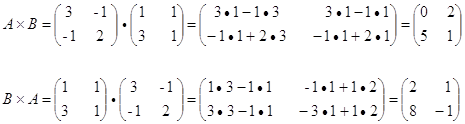
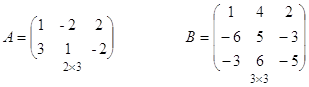
0 комментариев