Тольяттинский Государственный Университет
Задачи по Математическому моделированию
Студент: Шелудяков И.В.
Группа: М-402
Преподаватель: Бобровский А.В.
Тольятти 2006г.
Материал инструмента: Р6М5
Материал заготовки: Чугун СЧ 21-40
Станок: Вертикально-сверлильный 2Н125
Nшп=45…2000 об/мин
S=0,1-1,6 мм/об
Nэд = 2,2 кВт
![]() 25мм
25мм
t=1,5мм
Инструмент: зенкер насадной со вставными ножами из быстрорежущей стали ГОСТ 2255-71
d=22-40 мм
L=60-100 мм
D=50-100 мм
Ограничения по:
Стойкости
Мощности привода станка
Кинематике
Ограничение по стойкости
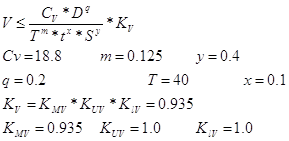 ,
, 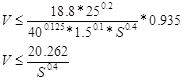

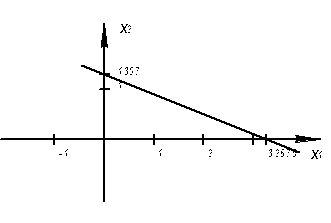
Ограничение по мощности привода
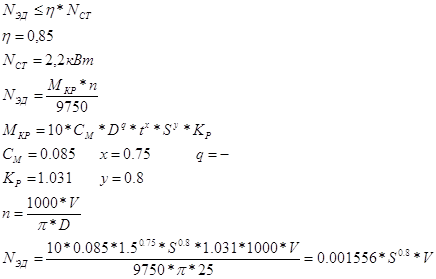
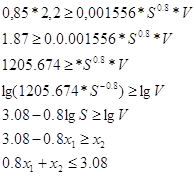
Ограничение по кинематике станка
Sобmin ≤ S ≤ Sобmax, Sобmin ≤ S, Sобmax ≥ S
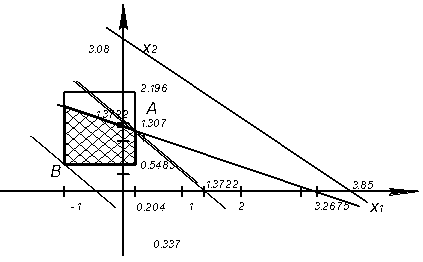
lg Sобmin ≤ lg Slg 0.1 ≤ x1x1 ≥ - 1
lg Sобmax ≥ lg Slg 1.6 ≥ x1x1 ≤ 0.204
![]()
![]() lg 3.534 ≤ x2x2 ≥ 0.5483
lg 3.534 ≤ x2x2 ≥ 0.5483
![]() lg 157.079 ≥ x2x2 ≤ 2.196
lg 157.079 ≥ x2x2 ≤ 2.196

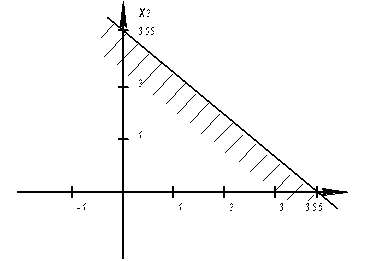
Целевая функция производительности
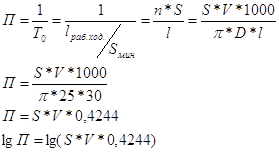
![]() - функция производительности.
- функция производительности.
Если z = 1, то x1 + x2 = 1.3722


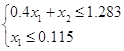

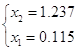
![]()
![]()
Симплекс – метод
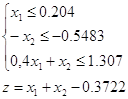
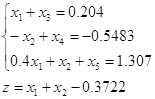
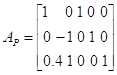

![]()
Выбираем базис и находим его решение:


Найдем алгебраические дополнения для каждого элемента матрицы

Союзная матрица Транспонированная матрица Обратная матрица
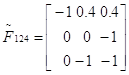
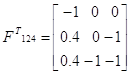
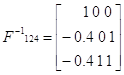
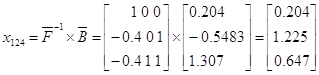
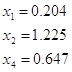
Базис 124 является допустимым т.к. все значения положительные.
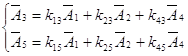

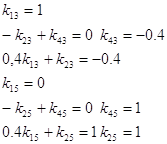
Найдем симплекс-разности.
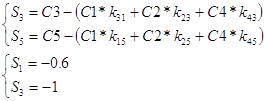
Решение является оптимальным.
Значения ![]() совпадают со значениями, полученными при решении задачи графическим способом.
совпадают со значениями, полученными при решении задачи графическим способом.
Симплекс-таблицы.

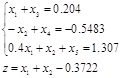 ,
, 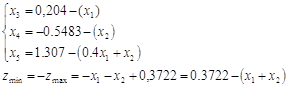
Табл. 1
| СН БН | СЧ | x1 | x5 |
| x3 | 0.204 | 1 | 0 |
| x4 | 0.7587 | 0.4 | 1 |
| x2 | 1.307 | 0.4 |
|
| zmin | 0.9348 | 0.6 | -1 |
![]()
Табл.2
| СЧ |
| x2 | |
| x3 | 0.204 | 1 |
|
| x4 | -0.5483 | 0 | -1 |
| x5 | 1.307 | 0.4 | 1 |
| zmin | 0.3722 |
| 1 |
Табл.3
| СН БН | СЧ | x3 | x5 |
| x1 | 0.204 | 1 | 0 |
| x4 | 0.6771 | -0.4 | 1 |
| x2 | 1.2254 | -0.4 | 1 |
| zmin | 0.8124 | -0.6 | -1 |
В табл.3 все элементы последней строки отрицательные - min найден.
Значения
![]() совпадают со значениями, полученными при решении задачи графическим способом и симплекс методом.
совпадают со значениями, полученными при решении задачи графическим способом и симплекс методом.
Похожие работы
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... определение базисных решений соответст- вует идентификации экстремальных точек , осуществляемой при геометрическом представлении пространства решений . Таким об- разом , максимальное число итераций при использовании симплекс- метода равно максимальному числу базисных решений задачи ЛП , представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не ...
... соответствующее этой точке, обычно называют начальным решением. От исходной точки осуществляется переход к некоторой смежной угловой точке. Выбор каждой последующей экстремальной точки при использовании симплекс-метода определяется следующими двумя правилами. Каждая последующая угловая точка должна быть смежной с предыдущей. Этот переход осуществляется по границам ( ребрам ) пространства решений ...
... - метод для решения задач линейного программирования. Задачи курсовой заботы: 1. привести теоретический материал; 2. на примерах рассмотреть симплекс метод; 3. представить данную курсовую работу в виде презентации. Математическое программирование Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи ...
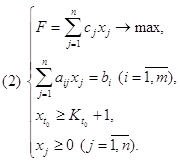

0 комментариев