Навигация
Критерий совместности общей системы линейных уравнений
5. Критерий совместности общей системы линейных уравнений
Как уже было отмечено, под общей системой линейных уравнений мы понимаем систему (2) в которой число неизвестных необязательно совпадает с числом уравнений.
Пусть дана общая система линейных уравнений (2) и требуется установить признак существования решения этой системы, т.е. условия, при которых система (2)является совместной.
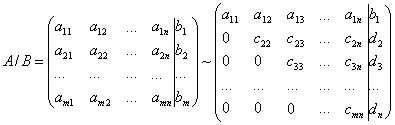
Из коэффициентов при неизвестных и свободных членов системы (2) составим матрицу
a11 a12 … a1n
A = a21 a22 … a2n……………………
am1 am2 … amn
которую назовем основной матрицей системы (2), и матрицу
a11 a12 … a1n b1
B = a21 a22 … a2n b2……………………… …… (13)
am1 am2 … amn bm
которую назовем расширенной матрицей системы (2).
Теорема 2.1. Для того чтобы система (2) линейных неоднородных уравнений была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу ее основной матрицы.
Доказательство. Необходимость. Пусть система (2) совместна и c1, c2,..., сп – некоторое ее решение. Тогда имеют место равенства:
![]()
а11с1 + а12с2 + …+ а1nсn = b1;
а21с1 + а22с2 + …+ а2nсn = b2;
. ……………………………………
аm1с1 + аm2с2 + …+ аmnсn = bm
из которых следует, что последний столбец расширенной матрицы (13) есть линейная комбинация остальных ее столбцов с коэффициентами с1, с2,..., сп. Согласно предложению 2, последний столбец матрицы В может быть вычеркнут без изменения ее ранга. При этом мы из матрицы В получим матрицу А. Таким образом, если ci, cz,..., сп — решение системы уравнении (2), то rang А = rang В.
Достаточность. Пусть теперь rang A = rang В. Покажем, что при этом система уравнений (2) совместна. Рассмотрим r базисных столбцов матрицы А. Очевидно, что они будут базисными столбцами и матрицы В. Согласно теореме о базисных строках и столбцах, последний столбец матрицы В можно представить как линейную комбинацию базисных столбцов, а следовательно, и как линейную комбинацию всех столбцов матрицы А, т.е.
b1 = а11с1 + а12с2 + …+ а1nсn;
![]() b2 = а21с1 + а22с2 + …+ а2nсn;
b2 = а21с1 + а22с2 + …+ а2nсn;
. …………………………………
bm = аm1с1 + аm2с2 + …+ аmnсn
где c1, c2,..., сп — коэффициенты линейных комбинаций. Таким образом, системе (14) удовлетворяют значения x1 = c1,..., хп = сп, следовательно, она совместна. Теорема доказана.
Доказанная теорема совместности системы линейных уравнений называется теоремой Кронекера – Капелли.
![]() Пример 1. Рассмотрим систему
Пример 1. Рассмотрим систему
5x1 – x2 + 2x3 + x4 = 7;
2x1 + x2 – 4x3 – 2x4 = 1;
x1 – 3x2 + 6x3 – 5x4 = 0.
Ранг основной матрицы этой системы равен 2, так как существует отличный от нуля минор второго порядка этой матрицы, а все миноры третьего порядка равны нулю. Ранг расширенной матрицы этой системы равен 3, так как существует отличный от нуля минор третьего порядка этой матрицы. Согласно критерию Кронекера – Капелли система несовместна, т.е. не имеет решений.
Используя критерий Кронекера – Капелли, проведем исследование системы двух линейных уравнений с двумя неизвестными x и y:
![]() a1x + b1y = c1,
a1x + b1y = c1,
a2x + b2y = c2. (13)
Основная матрица этой системы
a1 b1
a2 b2
имеет ранг r, причем 0 < r < 2.
Расширенная матрица
a1 b1 с1
a2 b2 с2
имеет ранг R, причем 0 < r < R. Очевидно, что r < R < r+1.
Имеют место следующие утверждения.
Пусть дана система двух линейных уравнений с двумя неизвестными (13). Тогда:
1. Если r = R = 0, т.е. если все коэффициенты a1, a2, b1, b2, c1, c2 равны нулю, то любая пара действительных чисел является решением системы (13).
2. Если r = 0, R = 1, т.е. a1 = a2 = b1 = b2 = 0 и c + c ≠ 0, то система (13) не имеет решений.
3. Если r =1, R = 1, то система (13) имеет бесконечно много решений, но не любая пара действительных чисел есть её решение.
4. Если r = 1, R = 2, то система (13) не имеет решений.
5. Если r = 2, R = 2, то система (13) имеет единственное решение, которое можно найти по правилу Крамера.
Справедливы и обратные утверждения.
1. Если система (13) имеет единственное решение, то r = R =2.
2. Если любая пара действительных чисел является решением системы (13), то r = R = 0.
3. Если система (13) не имеет решений, то r ≠ R, т.е. либо r =0 и
R = 1, либо r =1 и R = 2.
4. Если система (13) имеет бесконечно много решений, но не любая пара действительных чисел является её решением, то r = R = 1.
Приведём доказательство этих утверждений только в том случае, когда оба уравнения системы (13) являются уравнениями первой степени, т.е. когда выполняются условия a + b ≠ 0, a + b ≠ 0. В этом случае каждое уравнение этой системы в отдельности определяет прямую на плоскости, где задана система координат xOy. Это дает возможность придать геометрический характер дальнейшим рассуждениям при исследовании системы (13)
Теорема 2.2. Пусть две прямые заданы уравнениями
a1x + b1y – c1 = 0,
a2x + b2y – c2 = 0, (14)
где a + b ≠ 0, a + b ≠ 0.
1. Для того, чтобы две прямые пересеклись, необходимо и достаточно, чтобы r = R = 2.
2. Для того, чтобы две прямые были параллельными, но не совпадали, необходимо и достаточно, чтобы r = 1, R = 2.
3. Для того, чтобы две прямые совпадали, необходимо и достаточно, чтобы r = R = 1.
Доказательство. Сначала докажем достаточность условий.
1. Если r = R = 2, то система (14) имеет единственное решение, которое легко найти по правилу Крамера, а это означает, что прямые имеют одну общую точку, т.е. пересекаются.
2. Если r = 1, R = 2, то система (14) несовместна и поэтому прямые не имеют общих точек, т.е. параллельны и не совпадают.
3. Если r = R = 1, то все миноры второго порядка основной и расширенной матриц равны нулю, т.е.
a1 b1 = 0, c1 b1 = 0, a1 c1 = 0.
a2 b2 c2 b2 a2 c2
Эти условия можно переписать так:
a1b2 = b1a2, (15)
c1b2 = b1c2, (16)
a1c2 = c1a2. (17)
Рассмотрим теперь все возможные случаи.
а) Если а1 = 0, то b1 ≠ 0, так как a1 + b1 ≠ 0. Тогда из (15) следует, что а2 = 0, а так как a2 + b2 ≠ 0, то b2 ≠ 0. Тогда из (16) находим, что c1/b1 = c2/b2 = α и при этом уравнения прямых примут вид
b1(y – α) = 0, b2(y – α) = 0. Поскольку b1 ≠ 0, b2 ≠ 0, то отсюда вытекает, что эти прямые совпадают с прямой y – α = 0.
б) Если b1 = 0, то а1 ≠ 0, а из (15) тогда следует, что b2 = 0(причем
а2 ≠ 0). Тогда из (17) имеем c1/a1 = c2/a2 = β, и поэтому уравнения прямых примут вид а1(x – β) = 0, а2(x – β) = 0. Поскольку
а1 ≠ 0, а2 ≠ 0, то отсюда вытекает, что эти прямые совпадают с прямой x – β = 0.
в) Если а1 ≠ 0 и b1 ≠ 0, то из (15) вытекает, что а2/a1 = b2/b1 = γ, а из (16) и (17) вытекает, что с2 = b2c1/b1 = a2c1/a1. Т.е. получаем, что
а2 = γа1, b2 = γb1, c2 = γc1, и поэтому уравнения прямых примут вид
a1x + b1y – c1 = 0, γ(a1x + b1y – c1)= 0. Поскольку γ ≠ 0, то отсюда вытекает, что эти прямые совпадают.
Теперь докажем необходимость условий. Доказательство проведём методом от противного.
1. Пусть прямые пересекаются. Докажем, что r = R = 2. Если бы оказалось, что r = 1, R = 2, то по доказанному прямые были бы параллельны и не совпадали. Если бы оказалось, что r = R = 1, то по доказанному прямые оказались бы совпавшими.
Следовательно, r = R = 2.
2. Пусть прямые параллельны. Докажем, что r = 1, R = 2. Если бы оказалось, что r = R = 2, то по доказанному прямые оказались бы пересекающимися. Если бы оказалось, что r = R = 1, то по доказанному прямые оказались бы совпавшими.
Следовательно, r = 1, R = 2.
3. Пусть прямые совпадают. Докажем, что r = R = 1. Если бы оказалось, что r = R = 2, то по доказанному прямые оказались бы пересекающимися. Если бы оказалось бы, что r = 1, R = 2, то по доказанному прямые были бы параллельны.
Следовательно, r = R = 1.
Заключение
В данной работе я изучила пути решения систем линейных уравнений наиболее простые и быстрые, также весь материал я исследовала не только теоретически, но и практически, приводя некоторые примеры в тексте.
Список литературы
1. А. Дадаян. Алгебра и геометрия. / А.А. Дадаян, В.А. Дударенко.
2. Ф.Р. Гантмахер. Теория матриц (издание третье)./Ф.Р. Гантмахер.
3. Математический энциклопедический словарь.
4. Л. Андреева. Реферат по математике „Системы уравнений”. / Л. Андреева.
5. Д.К. Фадеев. „Сборник задач по высшей алгебре”./ Д.К. Фадеев, И.С. Саминский
Похожие работы
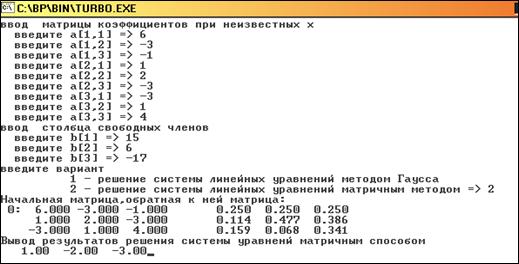
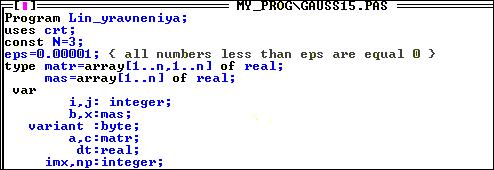
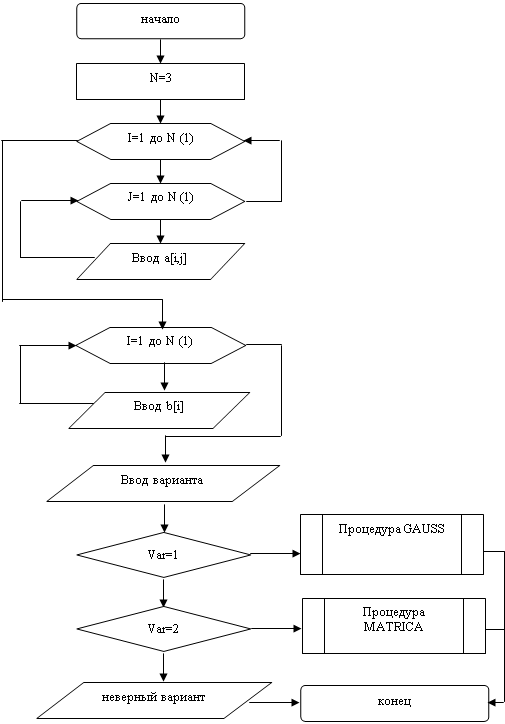
... 4.Исходный текст программы Составить программу решения систем линейных алгебраических уравнений с квадратной невырожденной матрицей порядка n методом Гаусса с использованием языка С++ . // Решение системы линейных уравнений методом Гаусса. #include<io.h> #include "stdio.h" #include "conio.h" #include <windows.h> #include <iostream> #include <time.h> #include ...
... строке матрицы i2-ю, умноженную на число r; процедура MultMatr предназначена для умножения матриц. Функция Sign используется для изменения знака на противоположный при вычислении обратной матрицы. Программа настроена на решение системы 3-х линейных уравнений с тремя неизвестными. Чтобы решить систему из 2-х уравнений с 2-мя неизвестными необходимо в программе изменить значение константы N с ...
... к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Рассмотрим решение системы (1) m линейных уравнений с nпеременными в общем виде: (3) Если m=n, то рассмотрим расширенную матрицу. Учитывая правую часть, приведем данную матрицу к треугольному виду: Ситема линейных ...
... Вывод Программа, разработанная в данной курсовой работе, реализует метод Зейделя для решения СЛАУ 6-го порядка. Она даёт гарантированно правильное решение системы линейных уравнений, если каждый элемент главной диагонали матрицы коэффициентов является единственным максимальным в своей строке, ненулевым, либо справедливы условия: максимальный элемент строки является единственным максимальным в ...
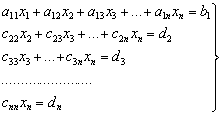
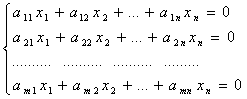




0 комментариев