Московский авиационный институт
/государственный университет/
Филиал «Взлет»
Курсовая работа
Теория вероятности и математическая статистика
Содержание
Задание №1: Проверка теоремы Бернулли на примере моделирования электросхемы
Задание №2: Смоделируем случайную величину, имеющую закон распределения модуля случайной величины, распределенной по нормальному закону
Задание №3: Проверка критерием Х2: имеет ли данный массив соответствующий закон распределения
Список используемой литературы
Задание №1: Проверка теоремы Бернулли на примере моделирования электросхемы
Теорема Я. Бернулли: при увеличении количества опытов, частота появлений событий сходится по вероятности к вероятности этого события.
План проверки: Составить электросхему из последовательно и параллельно соединенных 7 элементов, рассчитать надежность схемы, если надежность каждого элемента: 0.6 < pi < 0.9. Расчет надежности схемы провести двумя способами. Составить программу в Turbo Pascal, при помощи которой мы будем проводить опыты, учитывая, что надежность каждого из элементов в пределах от 0.6 до 0.9. Высчитывать частоту безотказной работы схемы. Для этого мы вводим надежность каждого из элементов. Программа будет увеличивать число опытов от 1000 до 20000 через 1000 проверяя сколько из этих опытов окажутся успешными, т.е. схема работает, для этого проверяется условие когда x[i]<P[i] то присваиваем этому элементу логическую 1 т.е. элемент работает, а если условие не выполняется то элемент не работает, всё это проделывается для каждого из 7 элементов для этого данное условие задаётся при помощи цикла. Далее получаем количество успешных опытов и делим на количество проведённых получая при этом частоту безотказной работы данной схемы.
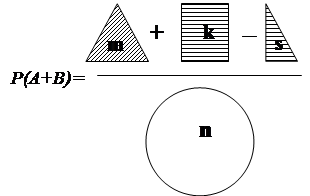
Схема:
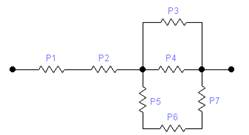
Электрическая цепь, используемая для проверки теоремы Бернулли
Расчет:
Чтобы доказать выполнимость теоремы Бернулли, необходимо чтобы значение частоты появления события в серии опытов в математическом моделировании равнялось значению вероятности работы цепи при теоретическом расчёте этой вероятности.
Математическое моделирование с помощью Turbo Pascal.
Program TVMS_kursov_1;
Uses CRT;
Var i,b,k,d,op,n:Integer;
ch:Real;
P,x:Array[1..10] of Real;
a:Array[1..30] of Integer;
Begin
ClrScr;
Randomize;
For i:=1 to 7 do
begin
Write(' Введите надёжности элементов P[',i,']=');
ReadLn(P[i]);
End;
WriteLn;
WriteLn('Число опытов ','Число благоприятных исходов ','Частота');
For op:=1 to 20 do
begin
n:=op*1000;
d:=0;
For k:=1 to n do
begin
For i:=1 to 7 do
begin
x[i]:=Random;
If x[i]<P[i] then a[i]:=1 else a[i]:=0;
End;
b:=((a[3]+a[4]+a[5]*a[6]*a[7])*a[1]*a[2]);
if b>=1 then d:=d+1;
End;
ch:=d/n;
WriteLn;
Write(' ':3,n:5,' ':20,d:5,' ':15,ch:5:4);
End;
WriteLn;
ReadLn;
End.
Результат работы программы.
Введите надёжности элементов P[1]=0.7
Введите надёжности элементов P[2]=0.9
Введите надёжности элементов P[3]=0.8
Введите надёжности элементов P[4]=0.6
Введите надёжности элементов P[5]=0.9
Введите надёжности элементов P[6]=0.7
Введите надёжности элементов P[7]=0.8
Таблица
| Числоопытов | Числоблагоприятныхисходов | Частота |
| 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 11000 12000 13000 14000 15000 16000 17000 18000 19000 20000 | 618 1225 1808 2478 3022 3592 4182 4847 5432 6070 6643 7252 7876 8574 9030 9769 10281 11006 11520 11997 | 0.6180 0.6125 0.6027 0.6195 0.6044 0.5987 0.5974 0.6059 0.6036 0.6070 0.6039 0.6043 0.6058 0.6124 0.6020 0.6106 0.6048 0.6114 0.6063 0.5998 |
Теоретический расчёт вероятности работы цепи:
I способ:
![]()
![]()
![]()
![]()
![]()
![]()
II способ:
![]()
![]()
![]()
Из математического моделирования с помощью Turbo Pascal видно, что частота появления события в серии
опытов сходится по вероятности к рассчитанной теоретически вероятности данного события ![]() .
.
Распределение модуля случайной величины, распределенной по нормальному закону
Пусть СВ Y подчиняется закону нормального распределения. Пусть по тем или иным причинам представляет интерес величина отклонения Y от нуля независимо от знака этого отклонения, т. е. СВ
X=|Y|
которая образует распределение модуля СВ, подчиненной нормальному закону.
Математическое выражение. Распределение модуля СВ определяется теми же двумя параметрами, которые характеризуют исходное нормальное распределение.
Плотность вероятности равна

где x0, σн — математическое ожидание и среднее квадратическое отклонение исходного нормального распределения;
φ(t) — функция, определяемая равенством (5.12).
Функция распределения равна
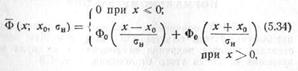
где Ф0(t) — функция, определяемая равенством (5.19).
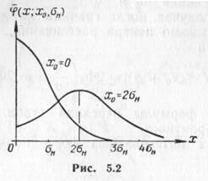
График плотности вероятности приведен на рис. 5.2.
Математическое ожидание, дисперсия и среднее квадратическое отклонение СВ Х определяются равенствами:

Вид распределения модуля случайной величины, распределенной по нормальному закону, зависит от соотношения между x0 и σн (рис. 5.2).
Для определения медианы нужно решить уравнение
![]()
а для определения моды — уравнение
![]()
Второе уравнение при x0> σн, а первое при любых x0 и σн решаются численными или графическими методами. При x0<σн мода равна нулю.
Формулы (5.33) и (5.34) можно выразить через срединное отклонение Ен исходного нормального распределения, заменив в них σн на Ен, φ(t) на φ^(t), Ф0(t) на Ф^0(t). Функции φ^(t) и Ф^0(t) определяются равенствами (5.13) и (5.21).
Вычисление: Расчеты по формулам (5.33) — (5.37) производятся с помощью табл. II и III. Если расчетчик предпочитает выражение исходного нормального распределения через срединное отклонение, то используются табл. IV и V.
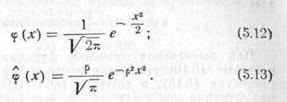
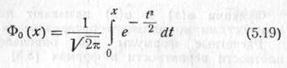
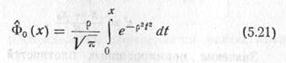
Задание №2: Смоделируем случайную величину, имеющую закон распределения модуля случайной величины, распределенной по нормальному закону
Программа в Turbo Pascal:
PROGRAM Kursov_2;
Uses Graph,Crt;
Var mi:array[1..100] of integer;
hi,pix,hn,hr,xi:array[1..200] of real;
m,i,l,j,n,a,b:integer;
mx,Dx,Gx,Sk,Ex,fx,xl,Dxs,Gxs,Sks,Exs:real;
xmin,xmax,pod,c,c1,c2,x,v:real;
st:string;
{---------------Генерирование числовых последовательностей-----------}
BEGIN
Randomize;
ClrScr;
Write(' Введите количество элементов последовательности: ' );
ReadLn(n);
a:=-3; b:=6;
WriteLn;
WriteLn(' Исходная последовательность с нормальным ');
WriteLn(' законом распределения на интервале [-3;6]:');
mx:=(a+b)/2;
Dx:=30/12;
for i:=1 to n do
begin
v:=0;
for j:=1 to 30 do
begin
x:=Random;
v:=v+x;
end;
v:=(v-15)/Sqrt(Dx)*1.5+mx;
hn[i]:=v;
Write(hn[i]:10:2);
end;
WriteLn;
ReadLn; ClrScr;
{-------------Минимальное и максимальное значения диапазона----------}
xmin:=hn[1]; xmax:=hn[1];
for i:=1 to n do
begin
if hn[i]>xmax then
xmax:=hn[i];
if hn[i]<xmin then
xmin:=hn[i];
end;
WriteLn;
WriteLn(' Максимальное значение:',xmax:6:2);
WriteLn(' Минимальное значение: ',xmin:6:2);
ReadLn; ClrScr;
{--Генерирование модyля CB с нормальным законом распределения--}
a:=0; b:=6;
WriteLn(' последовательность модyля CB с нормальным ');
WriteLn(' законом распределения:');
WriteLn;
for i:=1 to n do
begin
hr[i]:=abs(hn[i]);
Write(hr[i]:10:2);
end;
WriteLn;
ReadLn; ClrScr;
{-------------Минимальное и максимальное значения диапазона----------}
xmin:=hr[1]; xmax:=hr[1];
for i:=1 to n do
begin
if hr[i]>xmax then
xmax:=hr[i];
if hr[i]<xmin then
xmin:=hr[i];
end;
WriteLn;
WriteLn(' Максимальное значение:',xmax:6:2);
WriteLn(' Минимальное значение: ',xmin:6:2);
ReadLn; ClrScr;
{------------------------Разбивка на интервалы-----------------------}
m:=b-a;
c:=(xmax-xmin)/m;
c1:=xmin; c2:=c+xmin;
for i:=1 to m do
begin
xi[i]:=(c1+c2)/2;
mi[i]:=0; l:=1;
repeat
if (hn[l]<=c2) and (hn[l]>=c1) then
mi[i]:=mi[i]+1;
l:=l+1;
until l=n+1;
c1:=c2;
c2:=c2+c;
end;
GotoXY(1,8);
WriteLn('Kоличество чисел Чacтoтa пoпaдaния Bыcoтa cтoлбикa гиcтoгpaммы');
WriteLn;
for i:=1 to m do
begin
pix[i]:=mi[i]/n;
hi[i]:=pix[i]/c;
WriteLn(i,': ',mi[i]:6,pix[i]:20:3,hi[i]:22:3);
end;
ReadLn; ClrScr;
{----------------------Числовые характеристики-----------------------}
xl:=0;
for i:=1 to m do
xl:=xl+xi[i]*pix[i];
Dxs:=0;
for i:=1 to m do
Dxs:=Dxs+sqr(xi[i]-xl)*pix[i];
Gxs:=sqrt(Dxs); Sks:=0; Exs:=0;
for i:=1 to m do
begin
pod:=xi[i]-xl;
Sks:=Sks+pod*pod*pod*pix[i]/(Gxs*Gxs*Gxs);
Exs:=Exs+pod*pod*pod*pod*pix[i]/(Gxs*Gxs*Gxs*Gxs);
end;
Exs:=Exs-3;
GotoXY(10,1);
WriteLn(' Числовые характеристики:');
GotoXY(10,5);
WriteLn('Среднестатистическое значение xl= ',xl:6:3);
GotoXY(10,8);
WriteLn('Статистическая дисперсия Dxs= ',Dxs:6:3);
GotoXY(10,11);
WriteLn('Среднестатистическое отклонение Gxs= ',Gxs:6:3);
GotoXY(10,14);
WriteLn('Скошенность Sks= ',Sks:6:3);
GotoXY(10,17);
WriteLn('Островершинность Exs= ',Exs:6:3);
ReadLn;
END.
Результат работы программы:
Введите количество элементов последовательности: 300
Исходная последовательность с нормальным
законом распределения на интервале [-3;6]:
2.79 1.48 -0.18 2.84 -0.51 1.90 0.83 0.84
-1.50 0.43 3.67 1.30 2.61 1.22 -1.24 -0.49
2.14 -0.16 -2.01 4.72 3.08 1.14 0.84 0.24
-0.63 2.18 1.38 2.30 0.42 3.69 1.99 0.38
-1.14 0.77 1.68 -0.70 3.02 2.26 1.50 1.50
0.19 -0.19 1.61 1.92 2.63 0.76 1.28 1.90
4.41 -0.64 0.88 2.30 1.07 0.39 3.11 3.44
0.84 2.05 0.07 -0.56 1.77 0.77 1.21 2.08
-0.53 -0.03 0.78 -0.64 1.40 0.93 0.32 0.42
2.62 2.26 4.79 1.95 1.31 2.36 1.66 2.06
2.20 1.08 0.90 2.95 2.97 3.36 1.08 3.21
2.61 4.01 5.84 1.67 -0.49 2.06 0.64 2.29
-0.02 3.78 3.66 1.13 1.46 4.10 2.95 1.94
0.31 2.14 1.84 -0.40 0.84 1.89 1.88 3.47
2.51 -0.50 1.05 2.15 2.54 1.27 1.61 0.32
2.33 4.57 2.84 4.60 1.74 0.81 -1.28 -0.98
-1.84 -0.64 2.18 2.20 1.01 2.29 0.35 1.35
3.48 3.82 -0.07 1.14 1.99 -0.52 4.42 -0.34
1.43 -0.90 1.96 -1.30 -0.26 1.04 3.47 3.58
-0.95 1.68 -0.60 4.30 -0.96 1.19 1.94 1.23
0.76 1.84 0.05 0.69 1.18 1.68 1.04 1.07
2.87 1.66 0.96 2.88 4.11 0.49 0.82 1.71
-0.67 0.06 -0.98 3.26 2.56 1.49 3.09 1.43
1.77 2.30 2.44 2.06 3.33 0.26 0.19 4.09
2.69 -0.69 3.35 1.78 3.56 4.19 0.71 1.15
1.10 0.03 1.67 3.50 -1.51 3.16 0.18 -1.62
0.81 3.05 3.31 3.25 4.32 0.02 -2.65 0.79
0.07 1.51 1.30 2.49 -1.45 2.18 -0.03 3.27
1.21 -1.62 2.49 0.72 3.60 0.83 -0.67 2.11
3.15 1.83 3.02 0.27 0.61 6.20 -1.20 0.76
-1.34 0.68 -0.22 1.73 0.67 1.17 0.69 0.51
2.01 3.43 0.05 0.25 1.35 2.10 -0.29 -0.35
-0.22 2.33 1.67 2.72 3.85 0.15 1.16 2.09
2.14 1.93 -1.11 2.30 -1.10 1.21 2.00 -0.48
0.34 0.25 2.35 1.31 0.11 3.29 3.36 2.78
1.91 4.10 2.28 0.89 3.27 3.25 3.06 0.25
3.25 -0.28 0.80 0.17 0.69 2.63 2.36 3.52
Максимальное значение: 6.20
Минимальное значение: -2.65
Последовательность модуля CB с нормальным
законом распределения
2.79 1.48 0.18 2.84 0.51 1.90 0.83 0.84
1.50 0.43 3.67 1.30 2.61 1.22 1.24 0.49
2.14 0.16 2.01 4.72 3.08 1.14 0.84 0.24
0.63 2.18 1.38 2.30 0.42 3.69 1.99 0.38
1.14 0.77 1.68 0.70 3.02 2.26 1.50 1.50
0.19 0.19 1.61 1.92 2.63 0.76 1.28 1.90
4.41 0.64 0.88 2.30 1.07 0.39 3.11 3.44
0.84 2.05 0.07 0.56 1.77 0.77 1.21 2.08
0.53 0.03 0.78 0.64 1.40 0.93 0.32 0.42
2.62 2.26 4.79 1.95 1.31 2.36 1.66 2.06
2.20 1.08 0.90 2.95 2.97 3.36 1.08 3.21
2.61 4.01 5.84 1.67 0.49 2.06 0.64 2.29
0.02 3.78 3.66 1.13 1.46 4.10 2.95 1.94
0.31 2.14 1.84 0.40 0.84 1.89 1.88 3.47
2.51 0.50 1.05 2.15 2.54 1.27 1.61 0.32
2.33 4.57 2.84 4.60 1.74 0.81 1.28 0.98
1.84 0.64 2.18 2.20 1.01 2.29 0.35 1.35
3.48 3.82 0.07 1.14 1.99 0.52 4.42 0.34
1.43 0.90 1.96 1.30 0.26 1.04 3.47 3.58
0.95 1.68 0.60 4.30 0.96 1.19 1.94 1.23
0.76 1.84 0.05 0.69 1.18 1.68 1.04 1.07
2.87 1.66 0.96 2.88 4.11 0.49 0.82 1.71
0.67 0.06 0.98 3.26 2.56 1.49 3.09 1.43
1.77 2.30 2.44 2.06 3.33 0.26 0.19 4.09
2.69 0.69 3.35 1.78 3.56 4.19 0.71 1.15
2.79 1.48 0.18 2.84 0.51 1.90 0.83 0.84
1.50 0.43 3.67 1.30 2.61 1.22 1.24 0.49
2.14 0.16 2.01 4.72 3.08 1.14 0.84 0.24
0.63 2.18 1.38 2.30 0.42 3.69 1.99 0.38
1.14 0.77 1.68 0.70 3.02 2.26 1.50 1.50
0.19 0.19 1.61 1.92 2.63 0.76 1.28 1.90
4.41 0.64 0.88 2.30 1.07 0.39 3.11 3.44
0.84 2.05 0.07 0.56 1.77 0.77 1.21 2.08
0.53 0.03 0.78 0.64 1.40 0.93 0.32 0.42
2.62 2.26 4.79 1.95 1.31 2.36 1.66 2.06
2.20 1.08 0.90 2.95 2.97 3.36 1.08 3.21
2.61 4.01 5.84 1.67 0.49 2.06 0.64 2.29
0.02 3.78 3.66 1.13
Максимальное значение: 5.84
Минимальное значение: 0.02
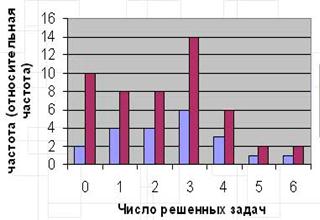
| № | Kоличество чисел | Чacтoтa пoпaдaния | Bыcoтa cтoлбикa гиcтoгpaммы | |
| 1: 2: 3: 4: 5: 6: | 71 81 59 35 16 2 | 0.237 0.270 0.197 0.117 0.053 0.007 | 0.244 0.278 0.203 0.120 0.055 0.007 | |
Числовые характеристики:
Среднестатистическое значение xl=1.664
Статистическая дисперсия Dxs=1.291
СреднестатистическоеотклонениеGxs=1.136
СкошенностьSks=1.193
Островершинность Exs= 0.449
Задание №3: Проверка критерием Х2: имеет ли данный массив соответствующий закон распределения
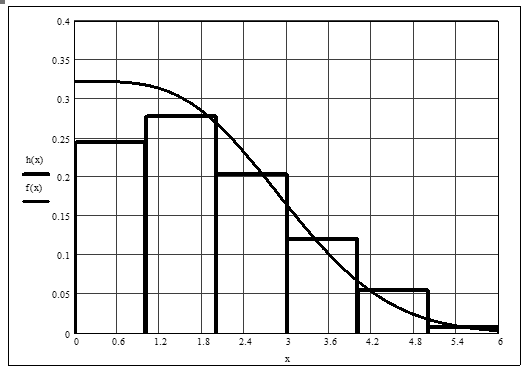
Гистограмма и сглаживающая функция


r=k-3=6-3=3,![]()
![]()
Вывод: Нет оснований принять гипотезу о распределении модуля случайной величины, распределенной по нормальному закону, так как
![]()
Список используемой литературы
1. «Теория вероятностей» В.С. Вентцель
2. «Теория вероятностей (Задачи и Упражнения)» В.С. Вентцель, Л.А. Овчаров
3. «Справочник по вероятностным расчётам»
4. «Теория вероятностей и математическая статистика» В.Е. Гмурман
5. «Руководство к решению задач по теории вероятностей и математической статистике» В.Е. Гмурман
Похожие работы
... оценками. Например, среднее арифметическое, медиана, мода могут показаться вполне приемлемыми для оценивания математического ожидания М (Х) совокупности. Чтобы решить, какая из статистик в данном множестве наилучшая, необходимо определить некоторые желаемые свойства таких оценок, т.е. указать условия, которым должны удовлетворять оценки. Такими условиями являются: несмещенность, эффективности ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...
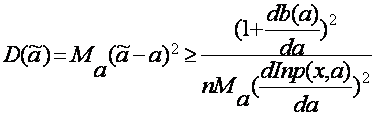
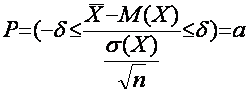
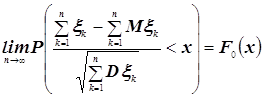



0 комментариев