Рефлексивность, т.е. каждая характеристическая функция эквивалентна себе u~u

1. Рефлексивность, т.е. каждая характеристическая функция эквивалентна себе u~u.

2. Симметрия, т.е. если u~u¹, то u¹~u.

3. Транзитивность, т.е. если u~u¹ и u¹~u², то u~u².

Одними из наиболее интересных способов решения коалиционных игр являются решения с применением аксиом Шелли.

3. Решение кооперативной игры при помощи вектора шепли

 

Аксиомы Шепли:

1. Аксиома эффективности. Если S - любой носитель игры с характеристической функцией u, то

= u (S)

Иными словами, “справедливость требует", что при разделении общего выигрыша носителя игры ничего не выделять на долю посторонних, не принадлежащих этому носителю, равно как и ничего не взимать с них.

2. Аксиома симметрии. Для любой перестановки p и iÎN должно выполняться  (pu) = j_{i (}u), т.е. игроки, одинаково входящие в игру, должны “по справедливости” получать одинаковые выигрыши.

3. Аксиома агрегации. Если есть две игры с характеристическими функциями u¢ и u¢¢, то

j_{i (}u¢ + u¢¢) = j_{i (}u¢) + j_{i (}u¢¢),

т.е. ради “справедливости" необходимо считать, что при участии игроков в двух играх их выигрыши в отдельных играх должны складываться.

Определение. Вектором цен (вектором Шепли) игры с характеристической функцией u называется n-мерный вектор

j ₍u) = (j₁ (u), j₂ (u),..., j_n (u)),

удовлетворяющий аксиомам Шепли.

Существование вектора Шепли вытекает из следующей теоремы

Теорема. Существует единственная функция j, определённая для всех игр и удовлетворяющая аксиомам Шепли.

Определение. Характеристическая функция w_S (T), определённая для любой коалиции S, называется простейшей, если

w_S (T) =

Содержательно простейшая характеристическая функция описывает такое положение дел, при котором множество игроков S выигрывает единицу тогда и только тогда, когда оно содержит некоторую основную минимальную выигрывающую коалицию S.

Вектор Шепли содержательно можно интерпретировать следующим образом: предельная величина, которую вносит i-й игрок в коалицию T, выражается как u (T) - u (T \{i}) и считается выигрышем i-го игрока; g_{i (}T) - это вероятность того, что i-й игрок вступит в коалицию T \{i}; j_{i (}u) - средний выигрыш i-го игрока в такой схеме интерпретации. В том случае, когда u - простейшая,

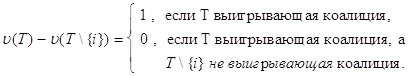
Следовательно

,

где суммирование по T распространяется на все такие выигрывающие коалиции T, что коалиция T \{i}не является выигрывающей.

Пример. Рассматривается корпорация из четырёх акционеров, имеющих акции соответственно в следующих размерах

a₁ = 10, a₂ = 20, a₃ = 30, a₄ = 40.

Любое решение утверждается акционерами, имеющими в сумме большинство акций. Это решение считается выигрышем, равным 1. Поэтому данная ситуация может рассматриваться как простая игра четырёх игроков, в которой выигрывающими коалициями являются следующие:

{2; 4}, {3; 4},

{1; 2; 3}, {1; 2; 4}, {2; 3; 4}, {1; 3; 4},

{1; 2; 3; 4}.

Найдём вектор Шепли для этой игры.

При нахождении j₁ необходимо учитывать, что имеется только одна коалиция T = {1; 2; 3}, которая выигрывает, а коалиция T \{1} = {2; 3} не выигрывает. В коалиции T имеется t = 3 игрока, поэтому

.

Далее, определяем все выигрывающие коалиции, но не выигрывающие без 2-го игрока: {2; 4}, {1; 2; 3}, {2; 3; 4}. Поэтому

.

Аналогично получаем, что , .

В результате получаем, что вектор Шепли равен . При этом, если считать, что вес голоса акционера пропорционален количеству имеющихся у него акций, то получим следующий вектор голосования , который, очевидно, отличается от вектора Шепли.

Анализ игры показывает, что компоненты 2-го и 3-го игроков равны, хотя третий игрок имеет больше акций. Это получается вследствие того, что возможности образования коалиций у 2-го и 3-го игрока одинаковые. Для 1-го и 4-го игрока ситуация естественная, отвечающая силе их капитала.

Заключение

Теория игр - наука, изучающая поведение многих участников, когда достигаемые каждым результаты зависят от действий остальных.

"Есть в современной математике одна область, она носит безобидное название теории игр, но ей, несомненно, суждено сыграть очень важную роль в человековедении самого ближайшего будущего, - говорил Джон фон Нейман, один из основоположников кибернетики. - Она занимается вопросами оптимального поведения людей при наличии противодействующего противника. Для ученого противник - это природа со всеми ее явлениями; экспериментатор борется со средой; математик - с загадками математического мира; инженер - с сопротивлением материалов".

Кооперативная теория игр, раздел игр теории, в котором игры рассматриваются без учёта стратегических возможностей игроков (тем самым кооперативная теория игр изучает некоторый класс моделей общих игр). В частности, в кооперативной теории игр входит исследование нестратегических (кооперативных) игр, лишённых с самого начала стратегического аспекта. В кооперативной игре задаются возможности и предпочтения различных групп игроков (коалиций) и из них выводятся оптимальные (устойчивые, справедливые) для игроков ситуации, в том числе распределения между ними суммарных выигрышей: устанавливаются сами принципы оптимальности, доказывается их реализуемость в различных классах игр и находятся конкретные реализации. В терминах кооперативных игр поддаются описанию многие экономические и социологические явления.

Список использованной литературы

1.         Большая советская энциклопедия, 1978 г.

2.         Теория игр - статья Миркина Б.Г. на портале "Экономика. Социология. Менеджмент".

3.         Дж. фон Нейман, О. Моргенштерн. Теория игр и экономическое поведение.