Навигация
На доске текст: “На дереве сидели 5 птичек, 3 птички улетели”
2. На доске текст: “На дереве сидели 5 птичек, 3 птички улетели”.
— Поставьте вопрос к данному условию. (Сколько птичек осталось?)
— Можно ли решить эту задачу так же, как домашнюю? (Нет. В домашней задаче 5 + 3 = 8, там есть слово “больше”, а здесь
птички улетели, их стало меньше.)
3. На доске текст: “На одном столе лежало 5 карандашей. Сколько карандашей лежало на другом столе?”
— Дополните условие задачи, чтобы она решалась так же, как домашняя,
Опять дети обращаются к домашней задаче. Сопоставляют ее решение с условием и по аналогии дополняют условие предложенной задачи.
Приведенные способы проверки активизируют деятельность учащихся. Контролируя, учитель обучает. При этом он использует различные методические приемы, способствующие формированию умения решать задачи, — это сравнение задач, дополнение условия задачи вопросом, недостающими данными. Предложенные задания постепенно усложняются.
Дополнительные задания, связанные с проверкой домашнего задания, органически включаются в урок и служат достижению его цели.
Подбор заданий для индивидуальной самостоятельной работы
Проведение самостоятельной работы на уроках математики прочно вошло в практику начальной школы.
Самостоятельная работа проводится без непосредственной помощи учителя в процессе ее выполнения, но это вовсе не исключает, а, наоборот, предполагает руководящую роль учителя, так как проведение самостоятельной работы — это фактически решение той или иной дидактической задачи, которую ставит учитель на уроке. Это подготовка детей к изучению нового материала усвоение новых знаний, расширение и углубление их, формирование вычислительных навыков и другие задачи.
Учитель также может поставить перед собой задачу проверить знания, умения и навыки учащихся. В этом случае дается проверочная самостоятельная работа.
В процессе самостоятельной работы встречаются различные виды деятельности учащихся (самостоятельная деятельность по образцу, предложенному учителем, применение знаний в аналогичных условиях, творческая деятельность).
Организуя самостоятельную работу, учитель обычно предлагает всему классу общее задание или дифференцирует задания по вариантам (два или четыре). Задания в каждом из вариантов чаще всего аналогичны по содержанию и требуют от учащихся использования однородных способов выполнения работы (независимо от дидактической задачи и видов деятельности учащихся).
Время выполнения такой работы каждым учеником в классе, естественно, различно. Поэтому учащимся, которые быстро справились с заданием, учитель предлагает индивидуальную работу. В одном случае это просто увеличение объема работы, т. е. предлагается решить еще одно такое же уравнение, в другом случае то задание, требующее других способов решения, или задание на сообразительность. И в том и в другом случае ученик получает индивидуальное задание и выполняет его самостоятельно.
Итак, индивидуальная самостоятельная работа должна учитывать индивидуальные особенности ученика: темп его работы, способность к предмету. Обычно такие работы выполняют в классе сильные ученики. Иногда учитель сразу предлагает таким ученикам карточки с содержанием индивидуальной самостоятельной работы. Можно наблюдать и другую противоположность. Учитывая индивидуальные особенности, учитель предлагает карточки с заданием слабым ученикам или ученикам, у которых, по его мнению, есть пробелы в знаниях, а всему классу дает общее задание.
Из всего сказанного можно сделать вывод, что индивидуальные самостоятельные работы обычно выполняют одни и те же ученики (либо сильные, либо слабые), ученики же, темп работы которых совпадает с планируемым учителем, ограничены выполнением только самостоятельной работы.
Возникает вопрос: можно ли сделать так, чтобы предложенная самостоятельная работа могла бы по сути своей стать индивидуальной для каждого ученика? Творчески работающие учителя не ограничиваются в процессе обучения включением только самостоятельных работ. Осуществляя индивидуальный подход к учащимся, изучая и зная их способности и наклонности, они планируют на некоторых уроках проведение индивидуальных самостоятельных работ, подбирая для каждого ученика задания в соответствии с их возможностями. Если такая работа проводится систематически, то в процессе ее выполнения уровень самостоятельности ученика повышается, он может выполнять уже более сложные задания без помощи учителя. Но и в этом случае индивидуальная самостоятельная работа нацелена в основном на усвоение знаний, умений и навыков.
Самостоятельная работа обеспечивается с помощью "Дидактических материалов".
При проведении самостоятельных работ одним из наиболее наглядных пособий, применяемых на уроках математики, является таблицы. По своему основному назначению таблицы могут быть подразделены на справочные, иллюстрированные и рабочие, называемые также таблицами-заданиями.
Таблицы-задания, используемые на уроках алгебры наряду с дидактическими раздаточными материалами, а иногда и совместно с ними, позволяют организовать самостоятельную работу учащихся, сочетать фронтальную и индивидуальные формы работы при закреплении пройденного, организовать повторение и систематизировать изучение материала.
Удобно использовать таблицы-задания и при опросе учащихся у доски, а в ряде случаев при опросе и фронтальной проверке выполненных учащимися самостоятельных заданий.
В отдельных случаях при проведении самостоятельной работы с целью проверки усвоенного теоретического материала могут быть использованы и иллюстрированы таблицами.
Работа с использованием таблиц-заданий может строиться в форме устных упражнений проведённых фронтально, диктантов, самостоятельных письменных работ. Кроме того, по таблицам можно осуществлять и фронтальную проверку выполненной самостоятельной работы, в том числе с вызовом отдельных учащихся к доске.
Устная проверка знаний и умений учащихся
Широкое использование устной формы проверки знаний, умений и навыков учащихся обусловлено ее главным достоинством по сравнению с другими формами—непосредственным контактом между учеником и учителем в процессе проверки. Это дает возможность учителю следить за развитием мысли отвечающего, своевременно корректировать знания, устранять все сомнения относительно состояния знаний ученика, исправлять погрешности речи, учить логически грамотно строить изложение, правильно применять терминологию.
Но в то же время при устной проверке учитель испытывает затруднения в оценке выявленных знаний. Трудности в методическом отношении связаны с: отбором материала по содержанию, формой постановки вопросов, их количеством; зависимостью оценок, выставляемых различным учащимся одного и того же класса и разных классов от их общей успеваемости; 3) потерей внимания всего класса к ответу одного ученика. Поэтому при подготовке к устной проверке учитель должен тщательно отбирать материал по содержанию, заранее формулировать вопросы, определять требования к ответам учащихся.
Нельзя забывать, что функции проверки (контролирующая, обучающая, ориентирующая и воспитывающая) будут выполняться лишь в том случае, если школьники убеждены в необходимости, целесообразности и объективности проверки, в справедливости и доброжелательности учителя. На уроках математики устная проверка знаний учащихся осуществляется в виде фронтальной и индивидуальной проверки. При фронтальной устной проверке за короткое время проверяется состояние знаний учащихся всего класса по определенному вопросу или группе вопросов. Фронтальную устную проверку учителя используют для выяснения готовности класса к изучению нового материала, для определения сформированности понятий, для проверки домашних заданий, для поэтапной или окончательной проверки учебного материала, только что разобранного на уроке. Цель, которую ставит учитель при организации фронтальной проверки, определяет ее место на уроке, а объем, глубина и полнота проверяемого материала—время, отводимое на проверку.
Индивидуальная устная проверка позволяет выявить правильность ответа по содержанию, его последовательность, полноту и глубину, самостоятельность суждений и выводов, степень развития логического мышления, культуру речи учащихся. Эта форма проверки используется для текущего и тематического учета.
Письменная проверка знаний и умений учащихся
Письменная проверка позволяет за короткое время проверить знания большого числа учащихся одновременно. Ее специфическая особенность— большая объективность по сравнению с устной, так как легче осуществить равенство меры выявления знаний. Для письменной проверки можно выбрать общую для всех школ систему вопросов, определить критерии оценки работы учащихся, что приводит к более полному осуществлению контролирующей и ориентирующей функций проверки.
Основной недостаток письменной проверки знаний заключается в отсутствии непосредственного контакта между учителем и учеником в процессе ее осуществления, что не позволяет учителю непосредственно наблюдать за процессом мышления учащихся, в ограниченности ее содержания.
На основании анализа результатов письменной проверки имеется возможность дать сравнительную оценку знаний и развития, учащихся; выявить весь объем ошибок, допускаемых классом в целом по проверяемому материалу, на основании чего учитель может судить о достоинствах и недостатках применяемой им методики.
Для письменной проверки знаний, умений и навыков, учащихся всего класса требуется значительно меньше времени по сравнению с устной проверкой, но сам учитель должен затратить время на подготовку к ней и не определение результатов. Учащиеся в процессе письменной проверки должны проявить большую сосредоточенность, умение четко выражать мысли, владеть навыками письменной речи.
В начальной школе, важной задачей остаётся формирование у учащихся умения получать информацию на слух, запоминать, обрабатывать и преобразовывать эту информацию, а так же формирование грамотной и точной математической речи, правильное чтение числительных и математических выражений. Помогают достичь этих целей математические диктанты. Математический диктант активизирует внимание школьников, позволяет быстро проверить и оценить их знания и умения, является хорошим организующим элементом урока.
Математические диктанты помогают эффективно тренировать устойчивость внимания учащихся, оперативную память, умение сосредоточиться. Хочется отметить, что задания этих диктантов позволяют на только оценить знания и умения школьников, но и являются хорошим инструментом диагностики причин затруднения каждого ученика.
Если математические диктанты проводить регулярно, то они дисциплинируют учеников и обеспечивают систематический оперативный контроль за их работой.
Заключение
Цель курсового исследования достигнута путём реализации поставленных задач. В результате проведённого исследования по теме "Формы и методы проверки знаний, умений, навыков по математике начальных классов" можно сделать ряд выводов:
Управление процессом формирования общих учебных умений и навыков младших школьников будет успешным, если:
- этот процесс строится на понимании научных основ, структуры и особенностей учебно-познавательной деятельности детей младшего школьного возраста; основным результатом данного процесса выступает готовность выполнять действия, направленные на восприятие, логическое осмысление, переработку и применение учебного материала, способствующая развитию учебно-познавательной деятельности школьника;
- модель управления формированием общих учебных умений и навыков младших школьников основывается на системном, функциональном, синер-гетическом, рефлексивном подходах и включает целевой, содержательный, мотивационно-стимулирующий, организационно-методический, оценочно-результативный, рефлексивно-аналитический структурные компоненты;
- управление данным процессом осуществляется как целенаправленное, специально организованное взаимодействие участников образовательного процесса начальной школы, ориентированное на поиск, качественную разработку и практическую реализацию дидактических, методических идей формирования и развития умений и навыков учебного труда учащихся начальных классов в системе «урок — внеклассная работа — домашняя учебная работа».
Традиционно процесс обучения рассматривается как процесс взаимодействия учителя и учащихся, в ходе которого решаются задачи образования, воспитания и развития. К основным структурным компонентам, раскрывающим его сущность, относят цели обучения, содержание, деятельность преподавания и учения, характер их взаимодействия, принципы, методы, формы обучения.
В традиционном обучении содержание представлено в основном предметными знаниями, умениями, навыками. Под знаниями в обучении понимают основные закономерности предметной области, позволяющие человеку решать конкретные производственные, научные и другие задачи, т.е. факты, понятия, суждения, образы, взаимосвязи, оценки, правила, алгоритмы, эвристики, а также стратегии принятия решений в этой области.
Знания — это элементы информации, связанные между собой и с внешним миром. Свойства знаний: структурируемостъ, интерпретируемость, связность, активность.
Под умением понимают освоенный человеком способ выполнения действия, обеспеченный некоторой совокупностью знаний. Умение выражается в способности осознанно применить знания на практике. Умения: применяются; преобразуются для обеспечения гибкости или приспособления к изменившимся условиям; обобщаются; пересматриваются.
Навыки— это автоматизированные компоненты сознательного действия человека, которые вырабатываются в процессе его выполнения. Навык возникает как сознательно автоматизируемое действие и затем функционирует как автоматизированный способ его выполнения. То, что данное действие стало навыком, означает, что индивид в результате упражнения приобрел возможность осуществлять данную операцию, не делая ее выполнение своей сознательной целью.
Общеучебные умения и навыки - это такие умения и навыки, которым соответствуют действия, формируемые в процессе обучения многим предметам, и которые становятся операциями для выполнения действий, используемых во многих предметах и в повседневной жизни.
Для усвоения отдельных предметов необходимы так называемые узкопредметные умения и навыки. Им соответствуют такие действия, формируемые в каком-либо учебном предмете, которые могут становиться операциями для выполнения лишь других специфических действий этого предмета или смежных предметов.
Библиографический список литературы
1. Беспалько В.П. Слагаемые педагогической технологии. - М., 1999.
2. Демидова Т.Е., Чижевская Л.И. Методика обучения математики в начальных классах: Курс лекций: вопросы частной методики. – Брянск: БГУ, 2001.
3. Ильин Е.П. Умения и навыки: нерешенные вопросы // Вопросы психологии. - 1986. - № 2.
4. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: LINKA-PRESS, 1998.
5. Маркова А.К., Матис Т.А., Орлов А.Б. Формирование мотивации учения. - М., 1990.
6. Нурминский И.И., Гладышева Н.К. Статистические закономерности формирования знаний и умений учащихся. - М., 1991.
7. Полякова А.В. Усвоение знаний и развитие младших школьников / Под ред. Л.В. Занкова. - М., 1998.
8. Российская педагогическая энциклопедия. В 2 т. - М., 1993-1999.
9. Талызина Н.Ф. Педагогическая психология: Учеб. пособие для студ. сред. спец. учеб. заведений. - М., 1998.
10. Фридман Л.М. Психопедагогика общего образования: Пособие для студентов и учителей.- М., 1997.
[1] Российская педагогическая энциклопедия. В 2 т. т. 1- М., 1993-1999. С. 123.
[2] Фридман Л.М. Психопедагогика общего образования: Пособие для студентов и учителей. М., 1997. С. 45.
[3] Полякова А.В. Усвоение знаний и развитие младших школьников / Под ред. Л.В. Занкова. М., 1998.С. 79.
[4] Нурминский И.И., Гладышева Н.К. Статистические закономерности формирования знаний и умений учащихся. М., 1991.С. 102..
[5] Маркова А.К., Матис Т.А., Орлов А.Б. Формирование мотивации учения. М., 1990. С. 23-34.
[6] Беспалько В.П. Слагаемые педагогической технологии. М., 1999. С. 105.
[7] Ильин Е.П. Умения и навыки: нерешенные вопросы // Вопросы психологии. - 1986. - № 2.
[8] Талызина Н.Ф. Педагогическая психология: Учеб. пособие для студ. сред. спец. учеб. заведений. М., 1998. С. 235.
[9] Истомина Н.Б. Методика обучения математике в начальных классах. – М.: LINKA-PRESS, 1998.С. 31.
Похожие работы
... прежнем уровне. В экспериментальном классе, котором были проведены ряд зачетных уроков, повысился уровень знаний. В ходе написания выпускной квалификационной работы по теме « Зачет как одна из форм контроля знаний учащихся по алгебре в 8 классе» были реализованы поставленные цели и задачи. Гипотеза дала положительный результат. Таким образом, разнообразие форм проверки знаний и их сочетания в ...
... , которая, как правило, обусловливается уровнем развития ученика, содержанием педагогического процесса, подготовленностью учителя к применению того или иного метода и т.д. Одним из методов педагогического процесса является наказание — торможение негативных проявлений личности с помощью отрицательной оценки ее поступков, порождение чувства вины, стыда и раскаяния. Если после наказания воспитанник ...
... Однако и в подростковом, и в старшем школьном возрасте имеются еще значительные резервы их совершенствования”.(22,С.108) ГЛАВА 3. Экспериментальная работа по формированию самоконтроля в процессе обучения математике по системе Эльконина- Давыдова. Наша работа посвящена изучению одного из структурных элементов учебной деятельности- изучению самоконтроля младших школьников. Перед началом проведения ...
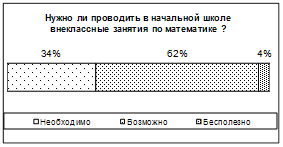
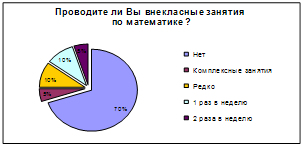
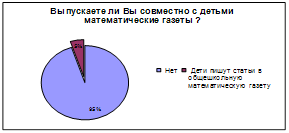
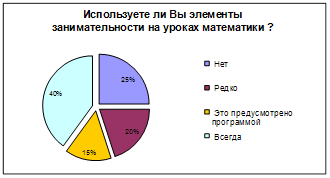
... и младших школьников. Анкета для студентов включала в себя два вопроса, один из которых о том, в чем, по их мнению, заключается развитие математических способностей школьников, а второй ¾ для выяснения отношения студентов к проведению внеклассной работы по математике в начальных классах. Анкета для преподавателей имела своей целью выяснить, проводят ли (а если проводят, то как часто) учителя ...

0 комментариев