Перевод мер угла в градусной системе
Классическая запись меры угла в градусной системе выглядит следующим образом: ![]() ,
,
Эта запись обозначает, что мера угла содержит А градусов, В минут и С секунд.
Но иногда необходимо выразить меру угла только в секундах или только в градусах. Возможна и другая ситуация, когда мера угла задано либо в градусах, либо в секундах, а нам необходимо записать эту меру в классической форме. Далее мы покажем, как это делается.
Перевод меры угла из классического вида в секунды
Для того, чтобы перевести меру угла, записанного в классическом виде, в секундный необходимо:
· Количество градусов А умножить на 3600,
· Количество минут В' умножить на 60,
· К количеству секунд С" прибавить ранее вычисленные значения.
В общем виде наши операции запишутся как:
![]()
Перевод меры угла из секундного вида в классический вид
Для перевода меры угла из секунд в классический вид, потребуется более сложный метод. Алгоритм (правила) перевода следующий:
Заданное число секунд S" делится на 3600 до целого числа. Этим самым мы вычисляем число градусов в мере угла S" / 3600 = A (до целого)
2. Умножаем полученное число градусов А на 3600 А1 = А * 3600
3. Из числа секунд S" вычитаем полученный результат умножения А1
S1" = S" - A1
4. Полученную разность S1" делим на 60 до целого, тем самым получаем число минут B' в мере угла B' = S1" / 60 (до целого).
5. Умножаем полученное число минут В' на 60 В1" = В' * 60
6. Вычитаем из числа S1" число B1" , и тем самым получаем число секунд С" в мере угла C" = S1" - B1"
7. Записываем меру угла в классическом виде ![]()
ПРИМЕР:
Задана мера угла, равная 19936. Привести ее к классическому виду.
РЕШЕНИЕ:
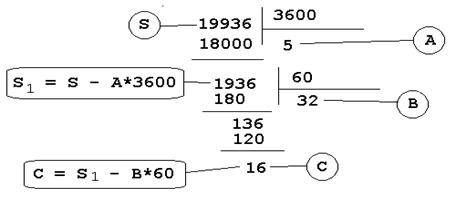
ОТВЕТ:
В классическом виде мера угла запишется как : ![]()
Перевод меры угла из классического вида в десятичный
Для перевода меры угла из классического вида в десятичный, проделаем следующие операции. Следует, однако, помнить, что при переводе меры угла в десятичный вид точность вычислений должна быть равна ![]()
1. Отделим градусную часть меры угла (А) от минутной (B') и секундной (C").
2. Преобразуем минутную часть меры угла (B') в секунды, для чего умножим ее на 60.
3. Сложим секундную часть меры угла (C") с полученным произведением.
4. Разделим полученную сумму на 3600, тем самым получаем десятичную часть меры угла.
5. Объединяем градусную часть меры угла и десятичную, отделив их запятой.
ПРИМЕР:
Мера угла представлена в классическом виде как ![]() . Представить ее в десятичном виде.
. Представить ее в десятичном виде.
РЕШЕНИЕ:
1. Отделим градусную часть меры угла А = 5;
4 Преобразуем минутную часть меры угла в секунды S1 = (B') * 60 = 32 * 60 = 1920
3. Сложим полученный результат с секундной частью S2 = (C") + S1 = 16 + 1920 = 1932.
4. Разделим полученный результат на 3600 D = S2 / 3600 = 1932 / 3600 = 0,53666667
5. Объединим между собой градусную часть меры угла и частное от деления. ![]()
Перевод меры угла из десятичного вида в классический вид
В десятичном виде меру угла можно записать следующим образом:
A,aaaaaaaa Где
А – целая часть меры угла
аааааааа – дробная часть меры угла.
Для перевода меры угла из десятичного представления в классическое представление мы поступаем следующим образом:
1. Отделяем целую и дробную части меры угла. После этого у нас получится два числа:
А – количество градусов в мере угла; ![]()
0,аааааааа – дробная часть числа.
2. Умножим получившуюся дробную часть на 60 ![]()
· Из получившегося числа отделим друг от друга целую и дробную части. После этого у нас получится два числа:
В (целая часть числа) представляет собой количество минут в мере угла ![]() 0,bbbbb – дробная часть числа
0,bbbbb – дробная часть числа
3. Умножим получившуюся дробную часть на 60 ![]()
Получившееся число представляет собой количество секунд в мере угла ![]()
4 Объединив градусную, минутную и секундную части, мы получим классический вид записи меры угла. ![]()
ПРИМЕР:
Мера угла представлена в десятичном виде как ![]() . Представить ее в классическом виде.
. Представить ее в классическом виде.
РЕШЕНИЕ:
1. Число градусов ![]() равно целой части меры угла, то есть
равно целой части меры угла, то есть ![]()
2. Составим дробь следующего вида ![]()
3. Умножим эту дробь на 60 ![]()
4. Число минут в мере угла ![]() равно целой части получившегося числа, то есть:
равно целой части получившегося числа, то есть: ![]()
5. Составим дробь следующего вида ![]()
6. Умножив эту дробь на 60, получим число секунд ![]() в мере угла
в мере угла ![]()
7. Объединив градусную, минутную и секундную части, мы получим классический вид записи меры угла. ![]()
ОТВЕТ: ![]()
Перевод мер угла в часовой системе
Классическая запись меры угла в часовой системе выглядит следующим образом:![]() ,
,
Эта запись обозначает, что мера угла содержит А часов, В минут и С секунд.
Но иногда необходимо выразить меру угла только в секундах или только в часах. Возможна и другая ситуация, когда мера угла задано либо в часах, либо в секундах, а нам необходимо записать эту меру в классической форме. Далее мы покажем, как это делается.
Перевод меры угла из классического вида в секунды
Для того, чтобы перевести меру угла, записанного в классическом виде, в секундный необходимо:
· Количество часов А(h) умножить на 3600,
· Количество минут В(m) умножить на 60,
· К количеству секунд С(s) прибавить ранее вычисленные значения.
В общем виде наши операции запишутся как: ![]()
Перевод меры угла из секундного вида в классический вид
Для перевода меры угла из секунд в классический вид, потребуется более сложный метод. Алгоритм (правила) перевода следующий:
Заданное число секунд S делится на 3600 до целого числа. Этим самым мы вычисляем количество часов в мере угла S / 3600 = A(h) (до целого)
2. Умножаем полученное число часов А(h) на 3600 А1 = А(h) * 3600
3. Из числа секунд S вычитаем полученный результат умножения А1 S1 = S - A1
4. Полученную разность S1 делим на 60 до целого, тем самым получаем число минут B(m) в мере угла B(m) = S1 / 60 (до целого).
5. Умножаем полученное число минут В(m) на 60 В1 = В(m) * 60
6. Вычитаем из числа S1 число B1 , и тем самым получаем число секунд С(s) в мере угла C(s) = S1 - B1
8. Записываем меру угла в классическом виде ![]()
ПРИМЕР:
Задана мера угла, равная 19936. Привести ее к классическому виду.
РЕШЕНИЕ:

ОТВЕТ:
В классическом виде мера угла запишется как : ![]()
Перевод меры угла из классического вида в десятичный
Для перевода меры угла из классического вида в десятичный, проделаем следующие операции. Следует, однако, помнить, что при переводе меры угла в десятичный вид точность вычислений должна быть равна ![]()
6. Отделим часовую часть меры угла (А(h)) от минутной (B(m)) и секундной (C(s)).
7. Преобразуем минутную часть меры угла (B(m)) в секунды, для чего умножим ее на 60.
8. Сложим секундную часть меры угла (C(s)) с полученным произведением.
9. Разделим полученную сумму на 3600, тем самым получаем десятичную часть меры угла.
10. Объединяем часовую часть меры угла и десятичную, отделив их запятой.
ПРИМЕР:
Мера угла представлена в классическом виде как ![]() . Представить ее в десятичном виде.
. Представить ее в десятичном виде.
РЕШЕНИЕ:
2. Отделим часовую часть меры угла А(h) = 5;
4 Преобразуем минутную часть меры угла в секунды S1 = (B(m)) * 60 = 32 * 60 = 1920
4. Сложим полученный результат с секундной частью S2 = (C(s)) + S1 = 16 + 1920 = 1932.
5. Разделим полученный результат на 3600 D = S2 / 3600 = 1932 / 3600 = 0,53666667
6. Объединим между собой градусную часть меры угла и частное от деления. ![]()
Перевод меры угла из десятичного вида в классический вид
В десятичном виде меру угла можно записать следующим образом:
A,aaaaaaaa Где
А – целая часть меры угла
аааааааа – дробная часть меры угла.
Для перевода меры угла из десятичного представления в классическое представление мы поступаем следующим образом:
4. Отделяем целую и дробную части меры угла. После этого у нас получится два числа:
А – количество часов в мере угла; ![]()
0,аааааааа – дробная часть числа.
5. Умножим получившуюся дробную часть на 60 ![]()
· Из получившегося числа отделим друг от друга целую и дробную части. После этого у нас получится два числа:
В (целая часть числа) представляет собой количество минут в мере угла ![]() 0,bbbbb – дробная часть числа
0,bbbbb – дробная часть числа
6. Умножим получившуюся дробную часть на 60 ![]()
Получившееся число представляет собой количество секунд в мере угла ![]()
4 Объединив часовую, минутную и секундную части, мы получим классический вид записи меры угла. ![]()
ПРИМЕР:
Мера угла представлена в десятичном виде как ![]() . Представить ее в классическом виде.
. Представить ее в классическом виде.
РЕШЕНИЕ:
8. Число градусов ![]() равно целой части меры угла, то есть
равно целой части меры угла, то есть ![]()
9. Составим дробь следующего вида ![]()
10. Умножим эту дробь на 60 ![]()
11. Число минут в мере угла ![]() равно целой части получившегося числа, то есть:
равно целой части получившегося числа, то есть: ![]()
12. Составим дробь следующего вида ![]()
13. Умножив эту дробь на 60, получим число секунд ![]() в мере угла
в мере угла ![]()
14. Объединив градусную, минутную и секундную части, мы получим классический вид записи меры угла. ![]()
ОТВЕТ: ![]()
Соотношения между градусной и часовой системами счисления
Как мы договорились, за единицу измерения меры угла мы выбрали угол, величина которого равняется одному обороту () Но мы знаем, что угол, равный одному обороту , содержит 360 градусной системы счисления или 24(h) часовой системы счисления. Таким образом, мы можем записать следующее соотношение: Из этого соотношения легко вывести и соотношение между единицами мер угла разных систем счисления. Полученные результаты занесем в таблицы.
Таблица соотношений между единицами мер угла.
Градусная система Часовая система
1 градус 4m (минуты)
1 минута (1') 4s (секунды)
1 секунда (1") 1/15 s (секунды)
Часовая система Градусная система
1 час (1h) 15 градусов
1 минута (1m) 15 минут (15')
1 секунда (1s) 15 секунд (15")
Похожие работы
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
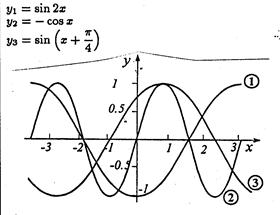
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
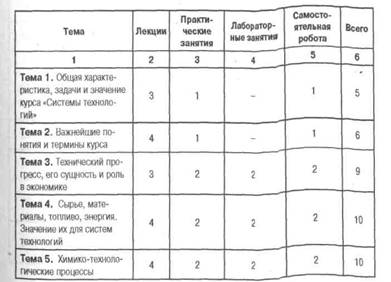
... ? 25. В чем сущность биохимических, фотохимических, радиационно-химических, плазмохимических процессов? Указать области их применения. 26. Какие основные группы физических процессов используют в системах технологий? 27. Дать определение машиностроению как комплексной области. Какова структура машиностроительного предприятия? 28. Раскрыть сущность понятий «изделие», «деталь», «сборочная единица ...
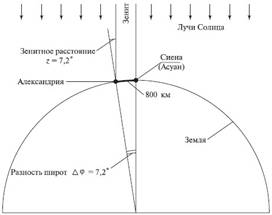
... вокруг нее. Луна же движется вокруг Земли с периодом обращения один месяц. В XVII в. Николай Коперник предложил гелиоцентрическую систему мира, согласно которой суточное движение светил вызвано вращением Земли вокруг оси, а те изменения, которые происходят на небе в течение года, связаны с обращением нашей планеты вокруг Солнца. Местное время. Вращаясь вокруг своей оси, Земля поворачивается за ...







0 комментариев