Навигация
4. Асимптоты функции
В предыдущих пунктах были рассмотрены методы исследования поведения функции с помощью производной. Однако среди вопросов, касающихся полного исследования функции, есть и такие, которые с производной не связаны.
Так, например, необходимо знать, как ведет себя функция при бесконечном удалении точки ее графика от начала координат. Такая проблема может возникнуть в двух случаях: когда аргумент функции уходит на бесконечность и когда при разрыве второго рода в конечной точке уходит на бесконечность сама функция. В обоих этих случаях может возникнуть ситуация, когда функция будет стремиться к некоторой прямой, называемой ее асимптотой.
Определение. Асимптотой графика функции 
называется прямая линия, обладающая тем свойством, что расстояние от графика до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Различают два типа асимптот: вертикальные и наклонные.
К вертикальным асимптотам относятся прямые линии 
, которые обладают тем свойством, что график функции в их окрестности уходит на бесконечность, то есть, выполняется условие: 
. Очевидно, что здесь удовлетворяется требование указанного определения: расстояние от графика кривой до прямой стремится к нулю, а сама кривая при этом уходит на бесконечность. С таким поведением функций мы сталкивались в п. 11.1, когда речь шла о разрывах второго рода. Итак, в точках разрыва второго рода функции имеют вертикальные асимптоты, например, 
в точке 
. Следовательно, определение вертикальных асимптот функции совпадает с нахождением точек разрыва второго рода.
Наклонные асимптоты описываются общим уравнением прямой линии на плоскости, то есть 
. Значит, в отличие от вертикальных асимптот, здесь необходимо определить числа 
и 
.
Итак, пусть кривая 
имеет наклонную асимптоту, то есть при 
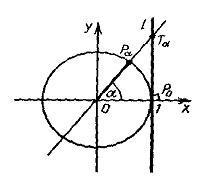
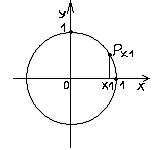
точки кривой сколь угодно близко подходят к прямой 
(рис. 4.1). Пусть 
– точка, расположенная на кривой. Ее расстояние от асимптоты будет характеризоваться длиной перпендикуляра 
. Согласно определению, 
. Но вычисляется довольно сложно, гораздо проще найти 
.
Из треугольника 
следует, что 
, так как 
. Значит, 
. Итак, 
.
Но выше было сказано, что 
, откуда следует, что 
. Вынесем 
в данном выражении за скобки: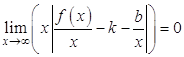 
. Так как по условию , то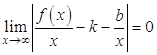 
. Здесь 
, следовательно, 
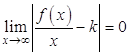, откуда получаем:
.
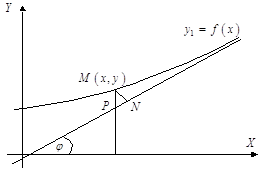
Рис. 4.1
Зная , рассмотрим снова предел: 
. Он выполняется лишь при условии, что
.
Таким образом, найдены и , а с ними и уравнение наклонной асимптоты. Если 
, то получаем частный случай горизонтальной асимптоты 
. При невозможности найти хотя бы один предел (при вычислении или ) делается вывод, что наклонной асимптоты нет.
Аналогично проводится исследование и при 
.
5. Общая схема исследования функций
На основании приведенных результатов можно провести полное исследование функции с качественным построением ее графика. План этого исследования следующий:
1) находят область определения функции;
2) определяют точки разрывов функции и их характер;
3) находят корни функции;
4) определяют четность или нечетность функции;
5) проверяют функцию на периодичность;
6) вычисляют производную функции, находят ее критические точки, находят интервалы монотонности и экстремумы;
7) вычисляют вторую производную функции и по ней определяют интервалы выпуклости, вогнутости и точки перегиба;
8) находят асимптоты функции;
9) по полученным данным строят качественный график исследуемой функции.
Литература
1. Зайцев И.А. Высшая математика. ДРОФА, 2005. – 400 с.
2. Краснов М. Вся высшая математика т. 1 изд. 2. Едиториал УРСС, 2003. – 328 с.
3. Мироненко Е.С. Высшая математика. М: Высшая школа, 2002. – 109 с.
4. Мироненко Е.С., Розанова С.А., ред., др, Розановой С.А., Кузнецова Т.А. Высшая математика. Изд-во: ФИЗМАТЛИТ®, 2009. – 168c.
5. Михеев В.И., Павлюченко Ю.В. Высшая математика. Изд-во: ФИЗМАТЛИТ®, 2007. – 200c.
6. Пак В.В., Носенко Ю.Л. Высшая математика. Сталкер, 1997. – 560 с.
Похожие работы
... функций обычно сводится к исследованию однозначных. Переменная величина у есть функция аргумента х, т.е. y=f(x), если каждому возможному значению х соответствует одно определённое значение у. Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f(x). Горизонтальную ось Ох называют осью абсцисс, вертикальную ось Оу - ...
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
... , тем ближе данный путь к критическому и наоборот и чем меньше коэффициент напряженности, тем большими резервами обладает данный путь [1]. Далее проводится анализ сетевого графика [2]. При этом определяется вероятность P наступления завершающего события в заданный срок. Для этого с помощью таблицы [3] определяется значение функции Лапласа Ф(Х): (6.12) ...
... математики в газете «Математика» и журнале «Математика в школе», а также соответствующей литературы, и заключаются в соблюдении современных требований к уроку. Основные направления совершенствования урока математики: 1. Современный урок математики характеризуется усилением функции управления процессом формирования новых знаний. Под управлением процессом формирования новых знаний ...
0 комментариев