Вариант 2
1. Решите уравнение 
Решение:
По определению 
.
Тогда 
и уравнение принимает вид 
откуда получаем 
.
Ответ: .
2. В урне находится 7 белых и 5 черных шаров. Найти вероятность того, что два одновременно изъятых шара будут белыми.
Решение:
Изначально в урне 12 шаров и вероятность извлечь первый шар белый составляет 
. После того как извлечен первый белый шар в урне остается 11 шаров, из них 6 белых, следовательно вероятность извлечь второй белый шар составит 
.
В итоге вероятность совместного появления двух белых шаров равна:
Ответ: 
.
3. В ящике 10 деталей, из которых 4 стандартные. Контролер взял наудачу 3 детали. Найти вероятность того, что хотя бы одна из изъятых деталей окажется стандартной.
Решение:
События «хотя бы одна стандартная» и «все детали не стандартные» противоположны и сумма их вероятностей равна 1.
Найдем вероятность того, что 3 извлеченных детали не стандартные.
Общее число возможных элементарных исходов выбора 3-х деталей из 10 равно числу сочетаний из 10 элементов по 3: 
, где 
, тогда 
Определим число исходов, благоприятствующих интересующему нас событию А (среди 3-х выбранных деталей 3 не стандартных). Три детали из 6 имеющихся можно выбрать 
способами следовательно, число благоприятствующих исходов 
.
Искомая вероятность равна отношению числа исходов, благоприятствующих нужному событию, к числу всех элементарных исходов: 
.
Тогда искомая вероятность того, что хотя бы одна из изъятых деталей окажется стандартной равна: 
Ответ: 
.
4. В коробке 7 карандашей, из которых 4 красные. Из этой коробки наудачу извлекается 3 карандаша. Х – число красных карандашей. Найти закон распределения случайной величины Х, функцию распределения и основные числовые характеристики.
Решение:
Среди 3-х извлеченных карандашей может быть 0, 1, 2 или 3 красных.
Найдем вероятность каждого исхода.
0 красных: 
1 красный: 
2 красных: 
3 красных: 
Закон распределения принимает вид:
| Х | 0 | 1 | 2 | 3 |
| р |
|
|
|
|
Запишем функцию распределения полученной случайной величины Х:
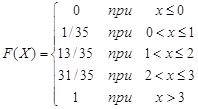
Математическое ожидание М(Х) дискретной случайной величины находится по формуле:
,
и подставляя данные получим:
Дисперсию дискретной случайной величины можно вычислить по формуле:
,
и, подставляя данные, получим:
Среднеквадратичное отклонение: s(Х)=
Ответ: 
;
;
5. По данной выборке постройте полигон. Найти эмпирическую функцию.
| Хi | 4 | 7 | 8 |
| Ni | 5 | 2 | 3 |
Решение:
Построим полигон частот – ломаную, соединяющую точки с координатами (Хi; Ni).
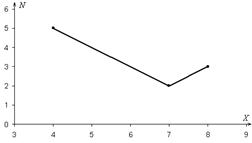
Объем выборки равен N = 5 + 2 + 3 = 10.
Найдем относительные частоты и составим эмпирическую функцию распределения:
| Хi | 4 | 7 | 8 |
| wi | 0,5 | 0,2 | 0,3 |
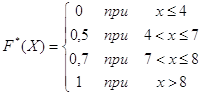
Ответ: решение выше.
Похожие работы
... , причём i – заводпоставляет mi% изделий (i = 1, 2, 3). Среди изделий i – го завода n1% первосортных. Куплено одно изделие. Оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено i – заводом. m1 = 60 m2 = 20 m3 = 20 n1 = 70 n2 = 80 n3 = 90 Пусть: H1 – поставил первый завод H2 – поставил второй завод H3 – поставил третий завод Пусть: ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...
... нашем примере: сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, она просто не в силах это сделать. Еще пример, выпадение снега в Москве 30 ноября является ...
... Первые два способа называются способами непосредственного подсчета вероятности, а классический основан на подсчете числа опытов благоприятствующих данному событию среди всех его возможных исходах. Основы теории вероятности Суммой событий Аi называется событие С состоящее в появлении события А или события В или их обоих вместе. Суммой события А и В называется событие С заключенное в ...
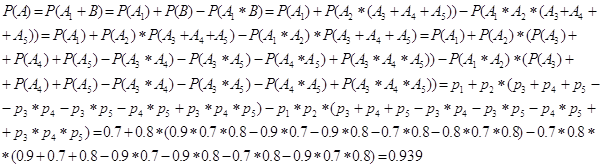
0 комментариев