Навигация
Вычисляют среднее квадратичное отклонение по формуле
13. Вычисляют среднее квадратичное отклонение по формуле
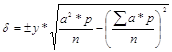
Пример
Имеются данные мужчин в возрасте 30-39 лет
| масса, кг х | Число обследованных р | Серединная варианта хс | а | а2 | а2*р | а*р | Накопленные частоты |
| 45-49 | 1 | 47,5 | -4 | 16 | 16 | -4 | 1 |
| 50-54 | 3 | 52,5 | -3 | 9 | 27 | -9 | 4 |
| 55-59 | 7 | 57,5 | -2 | 4 | 28 | -14 | 11 |
| 60-64 | 10 | 62,5 | -1 | 1 | 10 | -10 | 21 |
| 65-69 | 19 | 67,5 | 0 | 0 | 0 | 0 | 40 |
| 70-74 | 15 | 72,5 | 1 | 1 | 15 | 15 | 55 |
| 75-79 | 12 | 77,5 | 2 | 4 | 48 | 24 | 67 |
| 80-84 | 6 | 82,5 | 3 | 9 | 54 | 18 | 73 |
| 85-89 | 3 | 87,5 | 4 | 16 | 48 | 12 | 76 |
| сумма | 246 | 32 |
![]() - средняя арифметическая
- средняя арифметическая
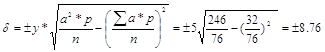 ; - среднее квадратичное отклонение;
; - среднее квадратичное отклонение; ![]() - ошибка средней
- ошибка средней
Статистическая оценка достоверности результатов медико-статистического исследования складывается из ряда этапов – точность результатов зависит отдельных этапов.
При этом встречаются две категории ошибок: 1) ошибки, которые нельзя заранее учесть математическими методами (ошибки точности, внимания, типичности, методические ошибки и т.д.); 2) ошибки репрезентативности, связанные с выборочным исследованием.
Величина ошибки репрезентативности определяется как объемом выборки, так и разнообразием признака и выражается средней ошибкой. Средняя ошибка показателя вычисляется по формуле:
![]() ;
;
где m – средняя ошибка показателя;
p – статистический показатель;
q – величина обратная p (1-p, 100-p, 1000-p, и т.д.)
n – число наблюдений.
При числе наблюдений менее 30 в формулу вводится поправка:
![]() ;
;
Ошибка средней величины исчисляется по формулам:
![]() ;
; ![]() ;
;
где s - среднее квадратичное отклонение;
n – число наблюдений.
Пример 1.
Из стационара выбыло 289 человек, умерло – 12.
Летальность составит:
![]() ;
; ![]() ;
;
![]()
При проведении повторных исследований средняя (М) в 68% случаев будет колебаться в пределах ±m, т.е. степень вероятности (p), с которой мы получим такие доверительные границы средней, равна 0,68. Однако такая степень вероятности обычно не удовлетворяет исследователей. Наименьшей степенью вероятности, с которой хотят получить определенные границы колебания средней (доверительные границы), является 0,95 (95%). В этом случае доверительные границы средней должны быть расширены путем умножения ошибки (m) на доверительный коэффициент (t).
Доверительный коэффициент (t) – число, показывающее, во сколько раз нужно увеличить ошибку средней величины, чтобы при данном числе наблюдений с желаемой степенью вероятности (p) утверждать, что средняя величина не выйдет за получаемые таким образом пределы.
При p=0.95 (95%) t=2, т.е. M±tm=M+2m;
При p=0.99 (99%) t=3, т.е. M±tm=M+3m;
Сравнение средних показателейПри сравнении двух средних арифметических (или двух показателей), вычисленных за различные периоды времени или в несколько отличающихся условиях, определяется существенность различий между ними. При этом применяется следующее правило: разница между средними (или показателями) считается существенной в том случае, если арифметическая разность между сравниваемыми средними (или показателями) будет больше, чем два квадратных корня из суммы квадратов ошибок этих средних (или показателей), т.е.
![]() (для сравниваемых средних);
(для сравниваемых средних);
![]() (для сравниваемых показателей).
(для сравниваемых показателей).
Определение достоверности средней при малом числе наблюдений (малая выборка).
При проведении исследований их объем не превышает 10-30 случаев. Такой объем наблюдений называется малым (или малой выборкой).
при определении статистической достоверности средней, полученной при малом числе наблюдений пользуются следующими формулами:
![]() ; где
; где ![]() ;
;
d – отклонение варианты (V) от средней величины (M),
n – число наблюдений;
t – доверительный коэффициент, определяемый по специальной таблице Стьюдента (приложение).
Пример.
Измерен пульс у 9 человек. Надо вычислить среднюю частоту пульса и определить ее статистическую достоверность.
1.Строиться вариационный ряд, вычисляется средняя (М) и среднее квадратичное отклонение (s).
| V | d=V-M | d2 |
| 63 | -5 | 25 |
| 68 | 0 | 0 |
| 65 | -3 | 9 |
| 65 | -3 | 9 |
| 60 | -8 | 64 |
| 70 | +2 | 4 |
| 70 | +2 | 4 |
| 75 | +7 | 49 |
| 76 | +8 | 64 |
| SV=612, n=9 | S=228 |
М=612/9=68 ударов в минуту
![]() удара в минуту
удара в минуту
2.Определяется ошибка средней арифметической величины
![]() удара в минуту
удара в минуту
2. Значение t определяется по таблице Стьюдента (см. приложение 1), где k=n-1, p- желаемая степень вероятности. в нашем примере число наблюдений 9, поэтому k=8, а желаемая степень вероятности p=0,95 (95%), тогда t=2.3
3. Устанавливаются пределы колебаний средней величины (ее доверительные границы): tm=1,9*2,3 » ±4. Следовательно, средняя величина пульса у 9 обследованных, равная 68 ударам в минуту, при проведении повторных исследований в 95% случаев будет колебаться в пределах 68±4, т.е. от 64 до 72 ударов.
Определение необходимого объема наблюдений.
В медицинских научных исследованиях часто используется выборочный метод. При этом изучается относительно малая часть всех возможных случаев, а полученные результаты (показатели, средние величины) рассматриваются в отношении всей совокупности. При обобщении всегда допускается некоторая ошибка, называемая предельной ошибкой выборки (D), которая представляет собой разницу между характеристиками генеральной и выборочной совокупности.
Предельно допустимая ошибка показателя (Dp) равна: Dp=рген.-рвыб.
Предельно допустимая ошибка средней Dх=`xген.-`xвыб.
Величина предельно допустимой ошибки вычисляется по формулам математической статистики:
1) для показателя: Dp=![]() , где Dp–предельная ошибка показателя,
, где Dp–предельная ошибка показателя,
p – величина показателя; q=1-p или 100-p или 1000-p в зависимости от основания к которому вычислен показатель;
n – число наблюдений;
t – доверительный коэффициент (при p=95% t=2, при p=99% t=3)
2) для средней: Dх= ![]() , где s - среднее квадратичное отклонение.
, где s - среднее квадратичное отклонение.
Из формул вычисления предельной ошибки выводятся формулы определения необходимого числа наблюдений в выборочном исследовании:
Dp=![]() , откуда n= t2*p*q/D2 (необходимое число наблюдений для получения показателя).
, откуда n= t2*p*q/D2 (необходимое число наблюдений для получения показателя).
Dх= ![]() , откуда n=t2*d2/D2; (необходимое число наблюдений для получения средней) Если в результате исследований конечный результата будет выражен абсолютными величинами (в сантиметрах, кг), необходимый объем наблюдений определяется по следующей формуле:
, откуда n=t2*d2/D2; (необходимое число наблюдений для получения средней) Если в результате исследований конечный результата будет выражен абсолютными величинами (в сантиметрах, кг), необходимый объем наблюдений определяется по следующей формуле: ![]() , где
, где
t = 2 (при p=95) или t = 3 (при p = 99),
D - предельно допустимая ошибка, выбирается исследователем.
d - среднее квадратичное отклонение
Среднее квадратичное отклонение определяется следующим образом:
1) если подобные исследования проводились , то берется из литературных источников,
2) если подобных исследований не проводилось, делается пробное исследование, при котором вычисляется d.
ПРИМЕР.
Нужно определить объем наблюдений, необходимый для того, чтобы получить достоверную среднюю величину роста семилетних мальчиков при p=0.95, t=2 и D=0,5 см.
Из приведенных ранее исследований известно, что d=5 см. Тогда n= 4*25/0,25=400, т.е. для получения достоверного результата следует взять группу, состоящую из 400 семилетних мальчиков.
Если в результате исследований конечный результат будет выражен в относительных величинах (например в %), необходимый объем наблюдений определяется по следующей формуле: ![]() ; где
; где
t = 2 (при p=95) или t = 3 (при p = 99),
D - предельно допустимая ошибка, выбирается исследователем.
p - коэффициент в %
q = 100% - p%.
Коэффициент p определяется следующим образом:
1) если подобное исследование проводилось ранее, то р берется из литературных источников;
2) если подобных исследований не проводилось, берется максимальное значение произведения p*q , которое получается, если p = q, т.е. p и q = 50%.
ПРИМЕР.Нужно определить объем наблюдений, необходимый для того чтобы получить достоверные данные о распространенности какого-то заболевания у студентов старших курсов медицинского института при P=95%, t=2 и D=3% Из литературных данных известно, что интересующее нас заболевание распространено в 30%, т.е. p=30%.
q = 100-30=70%, тогда n=4*30*70/9= 933, т.е. для получения достоверного результата следует иметь 933 наблюдения.
Если литературные данные отсутствуют, то n = 4*50*50/9 = 1111, т.е. для получения достоверного результата необходимое число наблюдений 1111.
В тех случаях, когда известна численность генеральной совокупности, могут быть использованы следующие формулы (для бесповторной случайной выборки):
n = N*t2*p*q / (N*D2+t2*p*q) , где N – численность генеральной совокупности.
Контрольные вопросы
1.Дайте определение вариационного ряда. Варианта. Средняя величина. Среднее квадратичное отклонение. Коэффициент вариации. Мода. Медиана.
2.Виды вариационных рядов. Особенности вычислениях основных характеристик.
3.Оценка достоверности.
4.Сравнение средних показателей
5.Определение достоверности средней при малом числе наблюдений
6.Расчет необходимого числа наблюдений.
ПРИЛОЖЕНИЕ
Таблица значений критерия t (Стьюдента)
| k (n-1) | Уровень вероятности р | ||
| 0,95 (95 %) | 0,99 (99 %) | 0,999 (99,9 %) | |
| 1 | 12,7 | 63,6 | 636,6 |
| 2 | 4,3 | 9,9 | 31,6 |
| 3 | 3,1 | 5,8 | 12,9 |
| 4 | 2,7 | 4,6 | 8,6 |
| 5 | 2,5 | 4,0 | 6,8 |
| 6 | 2,4 | 3,7 | 5,9 |
| 7 | 2,3 | 3,5 | 5,4 |
| 8 | 2,3 | 3,3 | 5,1 |
| 9 | 2,2 | 3,2 | 4,7 |
| 10 | 2,2 | 3,1 | 4,6 |
| 11 | 2,2 | 3,1 | 4,4 |
| 12 | 2,1 | 3,0 | 4,3 |
| 13 | 2,1 | 3,0 | 4,2 |
| 14 | 2,1 | 2,9 | 4,1 |
| 15 | 2,1 | 2,9 | 4,0 |
| 16 | 2,1 | 2,9 | 4,0 |
| 17 | 2,1 | 2,8 | 3,9 |
| 18 | 2,0 | 2,8 | 3,9 |
| 19 | 2,0 | 2,8 | 3,8 |
| 20 | 2,0 | 2,8 | 3,8 |
| 21 | 2,0 | 2,8 | 3,8 |
| 22 | 2,0 | 2,8 | 3,7 |
| 23 | 2,0 | 2,8 | 3,7 |
| 24 | 2,0 | 2,7 | 3,7 |
| 25 | 2,0 | 2,7 | 3,7 |
| 26 | 2,0 | 2,7 | 3,7 |
| 27 | 2,0 | 2,7 | 3,6 |
| 28 | 2,0 | 2,7 | 3,6 |
| 29 | 2,0 | 2,7 | 3,6 |
| 30 | 2,0 | 2,7 | 3,6 |
| ¥ | 1,9 | 2,5 | 3,3 |
ТЕСТЫ к практическому занятию по теме
«Средние величины, оценка разнообразия признака в вариационном ряду.
Оценка достоверности»
1. Средние величины применяются для характеристики признаков:
1) качественных;
2) количественных.
2. В отличие от статистических коэффициентов средние величины служат для изучения:
1) вероятностных признаков, которые могут быть или не быть;
2) постоянных признаков, присущих всем единицам наблюдения.
3. Симметричный вариационный ряд характеризуется распределением:
1) нормальным;
2) бимодальным.
4. Средняя арифметическая характеризует:
1) вариабельность признака;
2) распределение признака;
3) регрессию;
4) средний уровень;
5) репрезентативность;
6) взаимосвязь.
5. Средние величины используются для характеристики одного группового свойства статистической совокупности:
1) распределение количественных и качественных признаков в изучаемой совокупности ;
2) разнообразие или колебаемость любых признаков в совокупности;
3) взаимосвязь или зависимость между любыми признаками;
4) средний уровень признаков в совокупности;
5) репрезентативность или достоверность полученных результатов.
6. Поданным о числе дыханий в минуту из 12 наблюдений можно построить вариационный ряд:
1) простой, прерывный, четный;
2) нечетный: взвешенный, сгруппированный;
3) простой, непрерывный, симметричный.
7. Для определения среднего пульса у 100 больных рациональнее построить вариационный ряд:
1) сгруппированный, нечетный, непрерывный;
2) прерывный, взвешенный, сгруппированный;
3) несгрупированный, четный, взвешенный .
8. В симметричном ряду совпадают:
1) средняя арифметическая и мода;
2) медиана, мода и средняя арифметическая;
3) мода и медиана;
4) средняя арифметическая и медиана.
9. Средними величинами являются:
1) мода и медиана;
2) медиана и лимит;
3) лимит и мода.
10. В симметричном вариационном ряду совпадают:
1) М и Мо;
2) М, Мо и Ме;
3) М и Ме;
4) Ме и Мо .
11. В простом вариационном ряду средняя арифметическая рассчитывается по формуле:
1) ![]()
2) ![]()
3) ![]()
12. Формула для расчета средней арифметической взвешенного вариационного ряда по способу моментов:
1) ![]()
2) ![]()
3) ![]()
13. К критериям разнообразия признака в статистической совокупности относятся:
1) ошибка репрезентативности;
2) коэффициент вариации;
3) мода;
4) доверительные границы.
14. Среднее квадратическое отклонение характеризует:
1) средний уровень признака;
2) взаимосвязь;
3) вариабельность признака;
4) распределение признака.
15. К критериям вариабельности признака относятся:
1) М и Мо;
2) Мо и lim;
3) lim и V;
4) V и m.
16. Степень разнообразия нескольких признаков можно сравнить, рассчитав:
1) коэффициент вариации;
2) лимит;
3) доверительные границы;
4) коэффициент регрессии.
17. Правило "трех стигм" используется для оценки:
1) достоверности результатов исследования;
2) степени разнообразия признака;
3) взаимосвязи между признаками.
18. При значении коэффициента вариации (V), равном 15%, разнообразие признака:
1) слабое;
2) среднее;
3) высокое.
19. Степень разнообразия нескольких признаков можно сравнить, рассчитав:
1) ошибку репрезентативности;
2) лимит;
3) коэффициент вариации.
20. Амплитуда вариационного ряда дает информацию о:
1) разнообразие признака с учетом внутренней структуры совокупности;
2) разнообразие крайних вариант;
3)разнообразие вариант, превышающих среднюю арифметическую.
21. Для того, чтобы сравнить степень разнообразия длины тела новорожденных мальчиков и девочек наиболее целесообразно использовать критерии разнообразия:
1) лимит;
2) амплитуду;
3) среднее квадратическое отклонение.
22. Для того, чтобы сравнить степень разнообразия массы тела новорожденных и 7-летних детей наиболее целесообразно использовать:
1) амплитуду;
2) коэффициент вариации;
3) среднее квадратическое отклонение.
Установить соответствие
23. Формулы: Применение:
А. расчет среднего квадратического отклонения во взвешенном ряду;
Б. определение среднего квадратического отклонения в простом ряду при большом числе наблюдений;
Г. определение среднего квадратического отклонения во взвешенном ряду по способу моментов;
24. Показатель:
1) лимит;
2) средняя арифметическая;
3) среднее квадратическое Формула:
А)
Б) , где V-варианта
Д)
25. Статистические величины: Показатели:
1) средние; А. уровень заболеваемости;
2) относительные; Б. численность населения;
3) абсолютные. В. средняя продолжительность жизни;
Г. диагноз;
Д. пол.
26. При вероятности безошибочного прогноза Р = 87% результаты медико - биологических исследований:
1) достоверны;
2) недостоверны.
27. К критериям оценки достоверности относятся:
1) лимит и ошибка репрезентативности;
2) ошибка репрезентативности и доверительные границы;
3) доверительные границы и коэффициент вариации.
28. Критерий Стьюдента t = 3,4 свидетельствует о статистической:
1) достоверности;
2) недостоверности различия двух относительных величин.
29. Критерий Стьюдента, равный 1,5 свидетельствует о:
1) достоверности результатов исследования;
2) недостоверности результатов исследования.
30. При вероятности безошибочного прогноза р = 97% медико-биологические исследования статистические:
1) достоверны;
2) не достоверны.
31. При вероятности безошибочного прогноза р = 95% результаты медико-биологических исследований статистически:
1) достоверны;
2) не достоверны.
32. При вероятности ошибки Р = 3% результаты медико-биологических исследований:
1) достоверны;
2) не достоверны.
Похожие работы
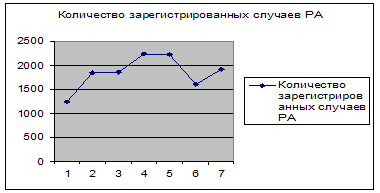
... При этом необходимо помнить, что сумма всех удельных весов должна равняться 1%, а сумма отрезков в градусах должна составлять 360°. Пример расчета интенсивного показателя. Население Ошской области за 2009 год составило 1088545 человек. Среди них 1241 случай РА. Чтобы определить показатель заболеваемости РА на 1000 населения, рассчитываем по формуле(см. выше) – 1241*1000/1088545=1,1 % Способы ...
... необходимым комплексом медицинских услуг. Создается сеть религиозных, благотворительных, меценатских и общественных организаций и фондов, которые содействуют расширению комплекса медико-социальных услуг. В страховой медицине осуществляется принцип солидарности “здоровый платит за больного, богатый — за бедного”. Медицинское страхование позволяет застрахованным получить дорогостоящую медицинскую ...
... . 4. Отрасли статистики. В процессе исторического развития в составе статистики как единой науки выделились и получили известную самостоятельность следующие отрасли: 1. Общая теория статистики, которая разрабатывает понятие категорий и методы измерения количественных закономерностей общественной жизни. 2. Экономическая статистика изучающая количественные закономерности процессов ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...

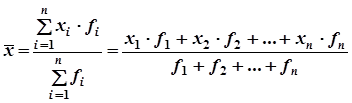
0 комментариев