Навигация
Если физический объем производства увеличился на 8%, то общие затраты на производство продукции увеличились на 6,81%
2. Если физический объем производства увеличился на 8%, то общие затраты на производство продукции увеличились на 6,81%.
3.Сумма экономии от среднего снижения себестоимости равна 94 тыс. руб.
Задание 4
Имеются следующие данные по 3 рынкам города о продаже яблок:
| Номер рынка | Продано яблок, тыс.р. | Цена 1 кг яблок, р. | ||
| июнь | август | июнь | август | |
| 1 | 2500 | 3000 | 35 | 30 |
| 2 | 1000 | 1200 | 32 | 25 |
| 3 | 1600 | 2000 | 34 | 30 |
Определите изменение средней цены на яблоки по 3 рынкам города всего и в т.ч. за счет:
- изменения цены на каждом рынке города;
- изменения, структуры продаж.
Решение
Составляем расчетную таблицу:
| Номер рынка | Продано яблок, тыс.р. | Цена 1 кг яблок, р. | Продано яблок, тыс. кг | р0q1 | |||
| июнь р0q0 | август р1q1 | июнь р0 | август р1 | июнь q0 | август q1 | ||
| 1 | 2500 | 3000 | 35 | 30 | 71,429 | 100,000 | 3500 |
| 2 | 1000 | 1200 | 32 | 25 | 31,250 | 48,000 | 1536 |
| 3 | 1600 | 2000 | 34 | 30 | 47,059 | 66,667 | 2266,7 |
| Сумма | 5100 | 6200 | 149,737 | 214,667 | 7302,7 | ||
Индекс цен переменного состава:

В целом цена уменьшилась на 15,2 % , т.е. на 34,060-28,882=5,178 руб.
Индекс цен постоянного состава:
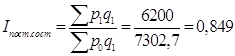
Средняя цена уменьшилась на 15,1 % из-за изменения цен на каждом рынке города, т.е на 34,060*0,151=5,143 руб.
Индекс структурных сдвигов в объеме продажи:

Из-за структурных изменений цена уменьшилась на 0,01 % т.е на 34,060*0,01= 0,341 руб.
Вывод.
В целом цена уменьшилась на 5,178 руб., т.е. на 15,2 %.
Средняя цена уменьшилась на 5,143 руб. из-за изменения цен на каждом рынке города, т.е на 15,1 %.
Из-за структурных изменений цена уменьшилась на 0,341 руб. т.е на 0,01 %.
Задание 5
Имеются следующие данные об изменении физического объема ВВП за период с 1990 г. (1990=100%):
| Показатели | 1991 | 1992 | 1993 | 1994 | 1995 |
| Индекс физического объема | 95,0 | 81,2 | 74,2 | 64,7 | 62,2 |
Определите, как в среднем ежегодно изменяется физический объем ВВП в указанном периоде. Исчислите цепные темпы изменения ВВП (в сопоставимых ценах).
Решение
В условии задачи даны базисные темпы изменения физического объема ВВП
Трбi= (уi/ y0 ) *100.
Среднее ежегодное изменение физического объема ВВП равно
![]()
В среднем ежегодно физический объем ВВП в указанном периоде уменьшается на 9,1%. Так как цепные темпы изменения вычисляются по формуле: Трцi= (уi/ yi-1 )*100, то цепные темпы изменения можно вычислить по формуле:
Трцi = Трбi / Трбi-1 *100.
Результаты вычислений представляем в таблице:
| Показатели | 1991 | 1992 | 1993 | 1994 | 1995 |
| Индекс физического объема | 95 | 85,474 | 91,379 | 87,197 | 96,136 |
| Цепные темпы изменения ВВП | 95 | 85,474 | 91,379 | 87,197 | 96,136 |
Задание 6
Имеются следующие данные о грузообороте предприятий транспорта и перевозке грузов предприятиями транспорта за 1986-1997 гг. в одном из регионов:
| Годы | Грузооборот предприятий транспорта, млрд ткм | Перевозка грузов предприятиями транспорта, млн.т. |
| 1986 | 280 | 285 |
| 1987 | 304 | 283 |
| 1988 | 270 | 321 |
| 1989 | 305 | 302 |
| 1990 | 301 | 316 |
| 1991 | 307 | 359 |
| 1992 | 296 | 334 |
| 1993 | 299 | 348 |
| 1994 | 296 | 333 |
| 1995 | 269 | 358 |
| 1996 | 310 | 305 |
| 1997 | 286 | 297 |
Для изучения связи между этими рядами произведите:
1. выравнивание рядов динамики по уравнению прямой;
2. вычислите коэффициент корреляции;
3. рассчитайте прогнозные значения грузооборота на 3 года вперед.
Сделайте выводы.
Решение
1. Воспользуемся прямолинейной формой связи регрессии, y= аt + b..
Оценки а и b можно искать по следующим формулам: 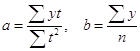 , где
, где ![]() - номер года и
- номер года и ![]() .
.
Для грузооборота предприятий транспорта составляем расчетную таблицу:
| Годы |
| Грузооборот предприятий транспорта, у |
|
|
| 1986 | -11 | 280 | 121 | -3080 |
| 1987 | -9 | 304 | 81 | -2736 |
| 1988 | -7 | 270 | 49 | -1890 |
| 1989 | -5 | 305 | 25 | -1525 |
| 1990 | -3 | 301 | 9 | -903 |
| 1991 | -1 | 307 | 1 | -307 |
| 1992 | 1 | 296 | 1 | 296 |
| 1993 | 3 | 299 | 9 | 897 |
| 1994 | 5 | 296 | 25 | 1480 |
| 1995 | 7 | 269 | 49 | 1883 |
| 1996 | 9 | 310 | 81 | 2790 |
| 1997 | 11 | 286 | 121 | 3146 |
| Итого | 0 | 3523 | 572 | 51 |
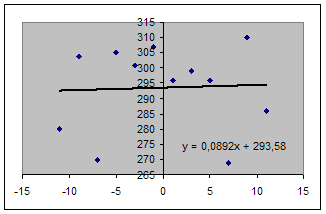
Подставляя итоги в формулы, получаем: а = 51/572=0,989, b = 3523/12=293,583
Уравнение регрессии: y = 0.989 t +293,583.
Найденное уравнение регрессии есть уравнение прямой, которая изображена на рис.
Для перевозки грузов предприятиями транспорта составляем расчетную таблицу:
| Годы |
| Перевозка грузов предприятиями транспорта, млн.т. |
|
|
| 1986 | -11 | 285 | 121 | -3135 |
| 1987 | -9 | 283 | 81 | -2547 |
| 1988 | -7 | 321 | 49 | -2247 |
| 1989 | -5 | 302 | 25 | -1510 |
| 1990 | -3 | 316 | 9 | -948 |
| 1991 | -1 | 359 | 1 | -359 |
| 1992 | 1 | 334 | 1 | 334 |
| 1993 | 3 | 348 | 9 | 1044 |
| 1994 | 5 | 333 | 25 | 1665 |
| 1995 | 7 | 358 | 49 | 2506 |
| 1996 | 9 | 305 | 81 | 2745 |
| 1997 | 11 | 297 | 121 | 3267 |
| Итого | 0 | 3841 | 572 | 815 |
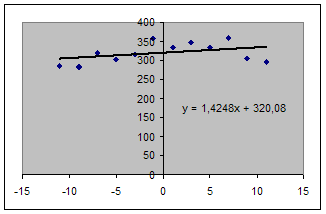
Подставляя итоги в формулы, получаем: а = 815/572=1,425, b = 3841/12=320,08
Уравнение регрессии: y = 1,425 t +320,08.
Найденное уравнение регрессии есть уравнение прямой, которая изображена на рис.
2. Вычисляем коэффициент корреляции по формуле:
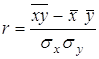 , где
, где ![]() ,
, ![]() .
.
Составляем расчетную таблицу:
| Годы | Исходные данные | Расчетные данные | |||
| Грузооборот предприятий транспорта, х | Перевозка грузов предприятиями транспорта, у | Х2 | Y2 | XY | |
| 1986 | 280 | 285 | 78400 | 81225 | 79800 |
| 1987 | 304 | 283 | 92416 | 80089 | 86032 |
| 1988 | 270 | 321 | 72900 | 103041 | 86670 |
| 1989 | 305 | 302 | 93025 | 91204 | 92110 |
| 1990 | 301 | 316 | 90601 | 99856 | 95116 |
| 1991 | 307 | 359 | 94249 | 128881 | 110213 |
| 1992 | 296 | 334 | 87616 | 111556 | 98864 |
| 1993 | 299 | 348 | 89401 | 121104 | 104052 |
| 1994 | 296 | 333 | 87616 | 110889 | 98568 |
| 1995 | 269 | 358 | 72361 | 128164 | 96302 |
| 1996 | 310 | 305 | 96100 | 93025 | 94550 |
| 1997 | 286 | 297 | 81796 | 88209 | 84942 |
| Итого | 3523 | 3841 | 1036481 | 1237243 | 1127219 |
| Средние | 293,5833 | 320,0833 | 86373,417 | 103103,58 | 93934,917 |
Получаем: ![]()
Так как коэффициент корреляции близок к 0, связь между признаками слабая.
3.Рассчитаем прогнозные значения грузооборота на 3 года вперед с помощью уравнения регрессии:
y = 293,583t +0.989:
у (13) = 0.989 * 13 + 293,583 = 306,362,
у (15) = 0.989 * 15 + 293,583 = 308,328,
у (17) = 0.989 * 17 + 293,583 = 310,294.
Задание 7
Имеются следующие данные по группе предприятий района:
| Пре дпри ятие | Стоимость основных производственных фондов, млн.руб. | Фондоотдача (выпуск продукции на 1 руб.основных производственных фондов), руб. | Производительность труда рабочих, тыс. руб. | Фондовооруж енность труда рабочих, тыс. руб. |
| 1 | 21,0 | 1,2 | 11,0 | 9,5 |
| 2 | 12,5 | 1,0 | 7,1 | 7,3 |
| 3 | 17,4 | 0,9 | 6,8 | 8,4 |
Определите по предприятиям района среднее значение:
1. стоимости основных производственных фондов на одно предприятие;
2. фондоотдачи;
3. производительности труда;
4. фондовооруженности труда
Решение
Составляем расчетную таблицу:
| Предпри ятие | Стоимость основных производственных фондов, ОФ | Фондоотдача, Фо | Производительность труда С | Фондовооруж енность труда рабочих, Фв | Выпуск В= ОФ* Фо | Количество рабочих N=В/С | Число рабо-чих Т=ОФ / Фв |
| 1 | 21 | 1,2 | 11 | 9,5 | 25,2 | 2,291 | 2,211 |
| 2 | 12,5 | 1 | 7,1 | 7,3 | 12,5 | 1,761 | 1,712 |
| 3 | 17,4 | 0,9 | 6,8 | 8,4 | 15,66 | 2,303 | 2,071 |
| Сумма | 50,9 | 53,36 | 6,354 | 5,994 |
1. Находим среднее значение стоимости основных производственных фондов на одно предприятие по формуле средней арифметической простой:
![]()
![]() 50,9/3 = 16,967 млн.руб.
50,9/3 = 16,967 млн.руб.
2.Находим среднее значение фондоотдачи по формуле средней арифметической взвешенной:
![]() руб.
руб.
3. Находим среднее значение производительности труда по формуле средней гармонической взвешенной: 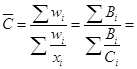 53,36/6,354=8,397 тыс. руб.
53,36/6,354=8,397 тыс. руб.
4. Находим среднее значение фондовооруженности труда по формуле средней гармонической взвешенной: 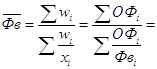 50,9/5,994=8,491 тыс. руб.
50,9/5,994=8,491 тыс. руб.
Задание 8
С целью определения средних затрат времени при поездках на работу населением города планируется выборочное наблюдение на основе случайного повторного отбора. Сколько людей должно быть обследовано, чтобы с вероятностью 0,954 ошибка выборочной средней не превышала 1 мин. При среднем квадратическом отклонении 15 мин.
Решение
Ошибка выборочной средней при повторном отборе вычисляется по формуле:![]() .
.
Так как Р = 0,954, то коэффициент доверия t=2.
По условию, среднее квадратическое отклонение ![]() .
.
Из неравенства ![]() получаем:
получаем: ![]()
Таким образом, должно быть обследовано не менее 900 человек.
Задание 9
Имеются следующие данные о среднедушевых доходах и расходах на продукты питания по совокупности семей в базисном и отчетном периодах:
| Показатель | Базисный период | Отчетный период |
| Среднедушевой доход за год, т. руб. | 40 | 45 |
| Расходы на продукты питания, т. руб | 28 | 33,5 |
Определите коэффициент эластичности расходов на питание в зависимости от роста дохода.
Решение
Определим коэффициент эластичности расходов на питание в зависимости от роста дохода по правилу:
Коэффициент эластичности =(Процентное изменение расходов на питание)/ (Процентное изменение роста дохода)
Среднедушевой доход за год увеличился на 45/40*100-100=12,5%.
Расходы на продукты питания увеличились на 33,5/28*100-100=19,6%.
Получаем: Коэффициент эластичности = 19,6 / 12,5 = 1,568.
При росте дохода на 1% расходы на питание увеличиваются на 1,568%.
Задание 10
Номинальные среднедушевые доходы населения одного из регионов составили в текущем периоде 2500 руб., за предыдущий период - 2100 руб.; доля налоговых платежей увеличилась с 20 до 22% соответственно. Цены выросли на 25%. Как изменились реальные доходы населения.
Решение
Индекс общей суммы номинальных доходов: ![]()
Индекс налогов: ![]()
Индекс цен: ![]()
Индекс общей суммы реальных доходов: ![]() .
.
Реальные доходы населения уменьшились на 6,4%.
Литература
1. Гусаров В.М. Статистика: Учебное пособие для вузов. - М.: ЮНИТИ-ДАНА, 2001.
2. Сборник задач по теории статистики: Учебное пособие/ Под ред.проф. В.В.Глинского и к.э.н., доц. Л.К. Серга. Изд.З-е.- М.:ИНФРА-М; Новосибирск: Сибирское соглашение, 2002.
3. Статистика: Учебное пособие/Харченко Л-П., Долженкова В.Г., Ионин В.Г. и др., Под ред. В.Г.Ионина. - Изд. 2-е, перераб. и доп. - М.: ИНФРА-М.2001.
4. Теория статистики: Учебник / Под ред. Р.А. Шмойловой,- М.-.Финансы и статистика, 2000.
5. Экономика и статистика фирм: Учебник /В.Е.Адамов, С. Д. Ильенкова, Т.П. Сиротина; под ред. С.Д. Ильенковой. - 2-е изд. - М.: Финансы и статистика, 1997.
Похожие работы
... экономико-рыночных отношений в нашей стране ставит перед школой новые задачи. Умение анализировать, сравнивать различные ситуации необходимо на сегодняшний день каждому современному человеку. Элективный курс «Общая теория статистики» с помощью математического аппарата даст начальные понятия о статистике, которые необходимы при решении управленческих задач. Курс рассчитан для учащихся 11 класса ...
... ; q1, q2 - объем отчетного, базисного периодов соответственно) для величины (цены) по каждому виду товара для величины q (объема) по каждому виду товаров: Найдем общие индексы по формулам: представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара. Общий индекс товарооборота равен: Найдем абсолютное ...

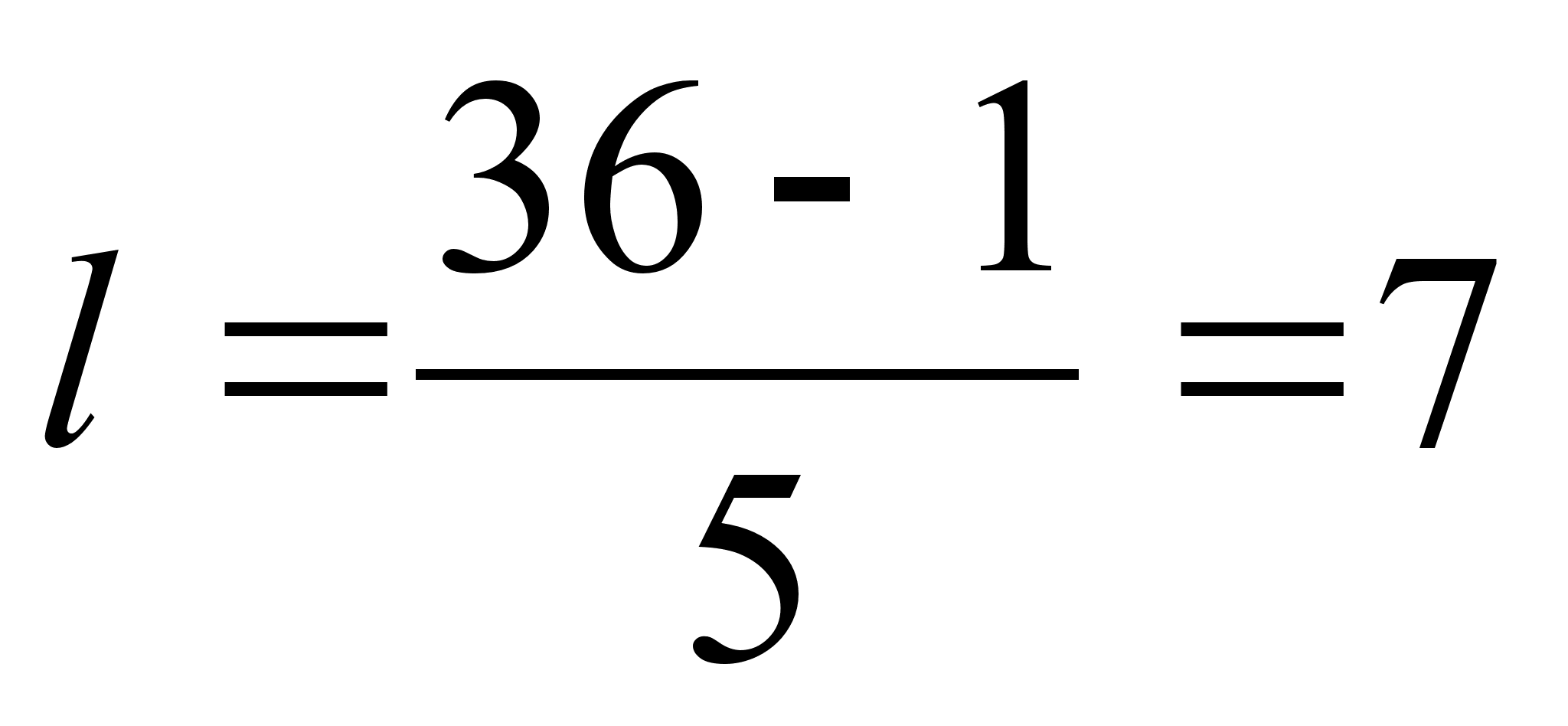
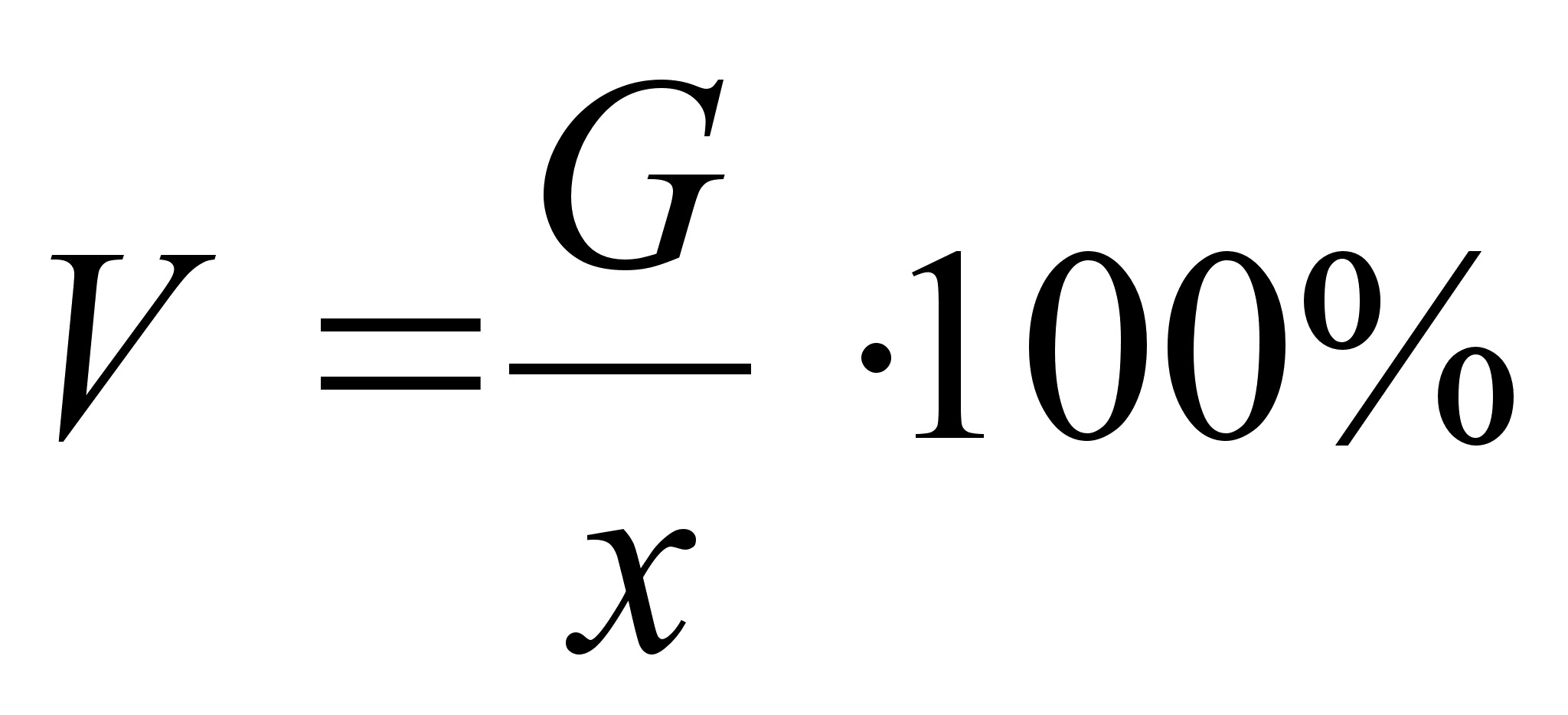
0 комментариев