УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
Кафедра бухгалтерского учета и аудита
Контрольная работа
по дисциплине «Эконометрика»
Исполнитель:
студентка группы ЭУВ 15141 УК
Мурсалимова Э.С.
Проверил:
Касьянов В. А.
Екатеринбург 2006
1. Исходные данные:
| год | годовые потребности свинины, кг | оптовая цена за кг, $ | доход на душу населения, $ | расходы по обработке мяса в % |
| 90 | 60 | 5 | 1300 | 60 |
| 91 | 62 | 4 | 1300 | 56 |
| 92 | 65 | 4,2 | 1500 | 56 |
| 93 | 62 | 5 | 1600 | 63 |
| 94 | 66 | 3,8 | 1800 | 50 |
2. Задание.
Построить модель вида:
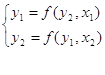
3. Решение.
Общий вид искомой модели:
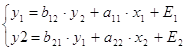 ,
,
a11, a22, b12, b21 – структурные коэффициенты.
Е1, Е2 – погрешность.
Пусть Е1=0 и Е2=0.
Таким образом, решение сводится к нахождению соответствующих структурных коэффициентов a11, a22, b12, b21.
Необходимо отметить, что искомая модель представляет собой систему взаимосвязанных уравнений. Ранг матрицы системы равен максимальному числу линейно – независимых переменных. В нашей системе таковыми являются x1, x2. Достаточным условием индентифицируемости системы является факт, что ранг матрицы системы не менее числа эндогенных переменных системы без единицы. Ранг матрицы равен 2, а число эндогенных переменных также 2 (у1, у2). Соответственно достаточное условие индентифицируемости системы выполняется. В связи с этим, для решения задачи необходимо применять косвенный метод наименьших квадратов.
Составим приведённую форму модели:
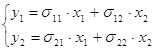
Выразим переменные через отклонения от средних уровней.
![]()
![]()
![]()
![]()
![]()
![]()
| y1 | y2 | х1 | х2 | y1*x1 | x12 | x1*x2 | y1*x2 | x22 | y2*x1 | y2*x2 |
| -3 | 0,6 | -200 | 3 | 600 | 40000 | -600 | -9 | 9 | -120 | 1,8 |
| -1 | -0,4 | -200 | -1 | 200 | 40000 | 200 | 1 | 1 | 80 | 0,4 |
| 2 | -0,2 | 0 | -1 | 0 | 0 | 0 | -2 | 1 | 0 | 0,2 |
| -1 | 0,6 | 100 | 6 | -100 | 10000 | 600 | -6 | 36 | 60 | 3,6 |
| 3 | -0,6 | 300 | -7 | 900 | 90000 | -2100 | -21 | 49 | -180 | 4,2 |
| 0 | 0 | 0 | 0 | 1600 | 180000 | -1900 | -37 | 96 | -160 | 10,2 |
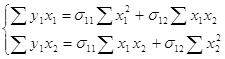
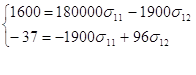
Решим систему в общем виде:
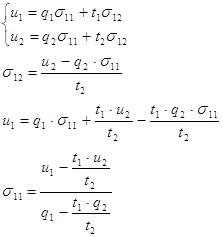
![]()
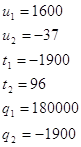
![]()
Итак первое уравнение имеет вид:
![]()
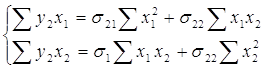
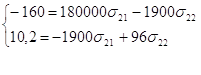
![]()
![]()
Итак,
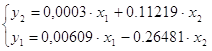
Приведем эту систему к виду
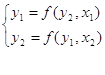
В общем виде:
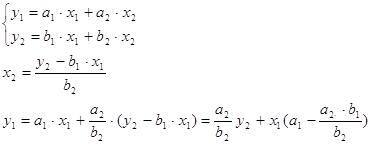
Оба уравнения по структуре одинаковы, следовательно для у2 просто меняем a на b, также при этом меняются индексы.
![]()
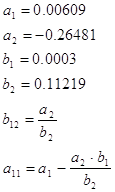
![]()
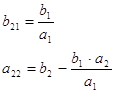
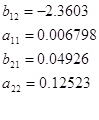
Искомая модель:
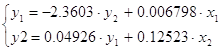
Похожие работы
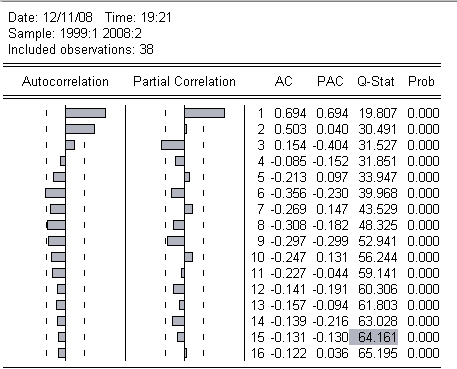
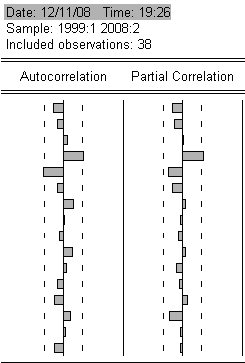
... no cross terms наблюдаемое значение оказывается меньше критического при уровнях значимости ,01 и ,005, из чего следует вывод об отсутствии гетероскедастичности в построенной модели. Проблему автокорреляции исследуем далее при помощи теста Бреуша-Годфри и Q-статистики Бокса-Льюнга. Результаты этих тестов представлены ниже: Breusch-Godfrey Serial Correlation LM Test: F-statistic 33.14949 ...
... оказывает определенное влияние на качество модели, однако ее устранение не является обязательным этапом, поэтому перейдем к дальнейшему исследованию качества регрессионной модели. 2. Исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка Переходим непосредственно к основной теме курсвой - проверяем модель на наличие гетероскедастичности. Для этого ...
... 1 2,32 38,8 114 2 2,19 39,9 101,1 3 2,83 30,1 153,8 4 2,75 31,7 146 5 2,59 17,2 124,8 6 2,27 39,7 103,6 7 2,05 36,9 119 8 1,95 38,2 108,7 9 2,08 40,1 106,5 Построение и анализ классической многофакторной линейной эконометрической модели 1. Спецификация модели 1.1 Идентификация переменных Многофакторная линейная эконометрическая модель устанавливает линейную ...
... . - то модель статистически значима. 2 - Отобрав из моделей все значимые модели, среди них находим самую точную, у которой минимальная средняя ошибка аппроксимации. Эконометрические модели для прогнозов исследуют поведение одного параметра работы предприятия во времени. I. Основная часть Параметрическая идентификация парной линейной эконометрической модели По семи областям региона ...
0 комментариев