Общий вид линейной однофакторной модели и её оценки
Оценка параметров модели методом 1МНК
Спецификация модели
Оценка тесноты связи между показателем Y и факторами Х1 и Х2, а также межу факторами. (Диаграмма рассеяния)
Коэффициенты частичной корреляции
Выводы о том, являются ли факторы ведущими и возможной мультиколлнеарности
Оценка параметров модели 1МНК в матричной форме
Коэффициенты множественной детерминации и корреляции для оцененной модели
Разложение коэффициента множественной детерминации на коэффициенты отдельной детерминации
Вычисление стандартных ошибок параметров и выводы о смещенности оценок параметров модели
Проверка значимости оценок параметров модели по критерию Стьюдента
Построение интервалов доверия для параметров модели
Доверительный интервал для прогноза рентабельности
Идентификация переменных
Исследование наличия мультиколлинеарности по алгоритму Феррара-Глобера
Навигация
Построение и анализ однофакторной эконометрической модели
Построение и анализ однофакторной эконометрической модели
38850
знаков
41
таблица
9
изображений
Задача 1. Построение и анализ однофакторной эконометрической модели
Однофакторная производственная функция накладных расходов в шахтном строительстве имеет вид
У=a0+a1x+e,
где У – накладные расходы, часть в затратах;
х – годовой объем затрат, тыс. грн;
На основании статистических данных по девяти шахтостроительным управлениям, используя 1МНК, найти оценки параметров производственной функции накладных расходов для шахтостроительного объединения. Дать общую характеристику достоверности и экономическую интерпритацию построенной модели.
Таблица 1 – Исходные данные
| № п\п | Накладные расходы | Объем работ |
| 1 | 27 | 15,6 |
| 2 | 30 | 15,3 |
| 3 | 28 | 14,9 |
| 4 | 29 | 15,1 |
| 5 | 26 | 16,1 |
| 6 | 25 | 16,7 |
| 7 | 28 | 15,4 |
| 8 | 26 | 17,1 |
| 9 | 25 | 16,8 |
Построение и анализ классической однофакторной эконометрической модели
1. Спецификация модели.
1.1 Идентификация переменных
Y – накладные расходы – результирующий показатель;
Х – объем работ – показатель-фактор;
Таблица 2 – Исходные данные и элементарные превращения этих данных для оценки модели.
| № п\п | Накладные расходы | Объем работ | Х*X | Y*Y | ОценкаУ | Отклонение, е | Предсказанное Y | Остатки |
| 1 | 27 | 15,6 | 243,36 | 729 | 27,64235 | -0,642345002 | 27,642345 | -0,642345 |
| 2 | 30 | 15,3 | 234,09 | 900 | 28,19401 | 1,805989034 | 28,19401097 | 1,805989 |
| 3 | 28 | 14,9 | 222,01 | 784 | 28,92957 | -0,929565584 | 28,92956558 | -0,9295656 |
| 4 | 29 | 15,1 | 228,01 | 841 | 28,56179 | 0,438211725 | 28,56178827 | 0,4382117 |
| 5 | 26 | 16,1 | 259,21 | 676 | 26,7229 | -0,722901729 | 26,72290173 | -0,7229017 |
| 6 | 25 | 16,7 | 278,89 | 625 | 25,61957 | -0,619569802 | 25,6195698 | -0,6195698 |
| 7 | 28 | 15,4 | 237,16 | 784 | 28,01012 | -0,010122311 | 28,01012231 | -0,0101223 |
| 8 | 26 | 17,1 | 292,41 | 676 | 24,88402 | 1,115984817 | 24,88401518 | 1,1159848 |
| 9 | 25 | 16,8 | 282,24 | 625 | 25,43568 | -0,435681147 | 25,43568115 | -0,4356811 |
| Сумма | 244 | 143 | 2277,4 | 6640 | 244 | 0 | 244 | 0 |
| Среднее | 27,11111111 | 15,88888889 | 253,04 | 737,78 | 27,11111 | - | 27,11111111 | - |
Похожие работы
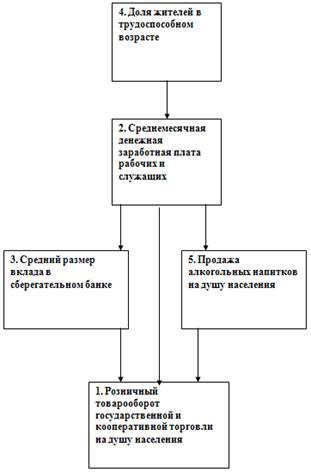
... 53951 20 55,04222 1,857778 21 54,61188 2,388125 22 54,44189 -1,74189 23 54,99919 -1,79919 24 53,51879 0,981207 25 54,09761 -2,99761 Вывод: в результате анализа однофакторной эконометрической модели, характеризующей взаимосвязь между долей жителей в трудоспособном возрасте и среднемесячной денежной заработной платой рабочих и служащих, можно отметить, что модель имеет высокую ...
... , что и в литературе встречается указание на то, что одним из свойств производственной функции является прохождение ее графика через начало координат, (9) свидетельствующее о невозможности выпуска продукции без использования производственных ресурсов. Исходя из сказанного, надо признать, что модели производственной функции линейного типа имеют ограниченную область применения. Поэтому в дальнейшем ...
... метод – 10-4-10-6 Микроскопия – 10-4-10-7 Метод фильтрации – 10-5-10-7 Центрифугирование – 10-6-10-8 Ультрацентрифугирование – 10-7-10-9 Ультрамикроскопия – 10-7-10-9 Нефелометрия – 10-7-10-9 Электронная микроскопия – 10-7-10-9 Метод диффузии – 10-7-10-10 Дисперсионный анализ широко используют в различных областях науки и промышленного производства для оценки дисперсности систем ( ...
... регрессией SSR = ∑(ỹ-y)2 = 3990,5; Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25; Общий разброс данных SSY = ∑(yi-y)2 = 5397,85; Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192; Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками. Вывод: Качество модели хорошее ...
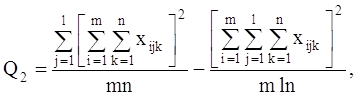
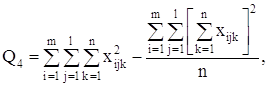
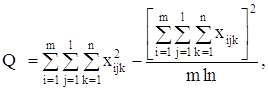
0 комментариев