Навигация
Решите задачу, используя критерий хи-квадрат
9. Решите задачу, используя критерий хи-квадрат.
Экспериментатору необходим идеальный кубик для чистоты эксперимента. Идеальный кубик – это кубик, каждая грань которого выпадала бы примерно равное число раз при достаточно большом числе подбрасываний. Задача состоит в выяснении того. Будет ли данный кубик близок к идеальному?
Для решения этой задачи кубик подбрасывали 60 раз. Выпадение граней распределилось следующим образом.
| Грани кубика | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота выпадения | 12 | 9 | 11 | 14 | 8 | 6 |
1. проверим выполнение ограничений: количество испытуемых в группе – 60 испытаний (60 > 20);
2. результаты занесены в таблицу. Число составляемых разрядов ƒ = 6;
3. сформулируем гипотезы:
Н 0: различия между данным кубиком и идеальным не значимы;
Н 1: различия между данным кубиком и идеальным значимы.
4. вычисления χ² проведем в таблице
| χ² | ƒi ΄ | ƒi ΄΄ | ƒi ΄- ƒi ΄΄ | (ƒi΄ - ƒi΄΄) ² | ƒi ΄ + ƒi ΄΄ | (ƒi΄ - ƒi΄΄) ² ƒi ΄ + ƒi ΄΄ |
| 1 | 12 | 10 | 2 | 4 | 22 | 0.18 |
| 2 | 9 | 10 | -1 | 1 | 19 | 0.05 |
| 3 | 11 | 10 | 1 | 1 | 21 | 0,05 |
| 4 | 14 | 10 | 4 | 16 | 24 | 0.67 |
| 5 | 8 | 10 | -2 | 4 | 18 | 0,22 |
| 6 | 6 | 10 | -4 | 16 | 16 | 1 |
| ∑ = 2,17 χ² = 2,17 |
5. по таблице 6 приложения найдем для к = 5 (к = ƒ - 1= 6 – 1 = 5) значение χ² (p ≤ 0,05) = 9,49.
Так как 2,17 < 9,49, то принимается гипотеза Н0: различия между частотами двух кубиков не значимы. Обе эмпирические совокупности можно считать выборками из одной генеральной совокупности.
10. Охарактеризуйте понятие «множественная корреляция».
Множественный коэффициент корреляции R (множественное R) - это положительный квадратный корень из R-квадрата. Эта статистика полезна при проведении многомерной регрессии (т.е. использовании нескольких независимых переменных), когда необходимо описать зависимость между переменными.
Множественный коэффициент корреляции характеризует тесноту связи между зависимой переменной и предиктором. Он изменяется в пределах от 0 до 1 и рассчитывается по формуле:
![]()
где ![]() - определитель корреляционной матрицы;
- определитель корреляционной матрицы;![]() - алгебраическое дополнение
- алгебраическое дополнение ![]() -го элемента.
-го элемента.
Наблюдаемое значение находится по формуле:
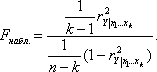
При небольшом числе наблюдений величина множественного коэффициента корреляции, как правило, завышается. Множественный коэффициент корреляции считается значительным, т.е. имеет место статистическая зависимость между ![]() и остальными факторами
и остальными факторами ![]() , если
, если
![]()
где ![]() определяется по таблице F-распределения.
определяется по таблице F-распределения.
Похожие работы
... , и , то можно предположить о правильном распределении объектов и уже существующих двух классах и верно выполненной классификации объектов подмножества М0. 3.2 Пример решения задачи дискриминантным анализом в системе STATISTICA Исходя из данных по 10 странам (рис. 3.1), которые были выбраны и отнесены к соответствующим группам экспертным методом (по уровню медицинского обслуживания), ...
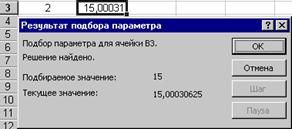
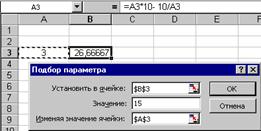
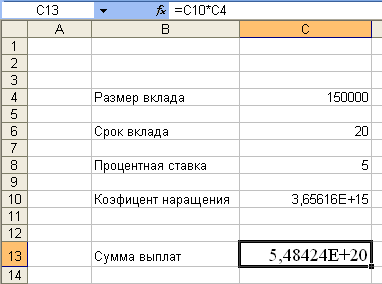
... ) или неположительным (второе решение). Задачу поиска параметра при налагаемых граничных условиях поможет решить специальная надстройка Microsoft Excel Поиск решения. 2 Практическая часть 2.1 Пример решения задач с использованием функции “подбор параметра” Как известно, формулы в Microsoft Excel позволяют определить значение функции по ее аргументам. Однако может возникнуть ситуация, ...
... его увеличением для целей информационного обеспечения исполнительных местных органов [7,8]. 3 ОПЫТ УПРАВЛЕНИЯ И ОБОЩЕНИЕ ДАННЫХ НА ПРИМЕРЕ АЛМАТИНСКОГО ОБЛАСТНОГО УПРАВЛЕНИЯ СТАТИСТИКИ3.1 Алматинское областное управление статистики как субъект сбора и обобщения статистической информации В своей деятельности Алматинское областное управление статистики (АОУС) руководствуется ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...

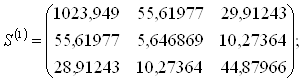

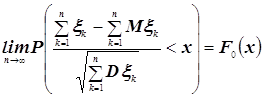
0 комментариев