Навигация
Расчет показателей корреляционного, дисперсионного анализа
35493
знака
43
таблицы
14
изображений
Задача 1. Корреляционный анализ
Исследовано функционирование некоторого предприятия торговли в течение n месяцев. Необходимо проанализировать наличие предполагаемой зависимости между: расходами предприятия на рекламу и продвижение товаров на рынок 
,
(в тыс. грн); расходами на обучение и повышение квалификации персонала Yi, (в тыс. грн.); объемом товарооборота предприятия торговли Ui, (в млн. грн.); прибылью предприятия Zi, (в тыс. грн.).
| X | Y | U | Z |
| 82 | 101 | 48 | 34 |
| 100 | 106 | 52 | 24 |
| 85 | 66 | 51 | 36 |
| 85 | 80 | 47 | 33 |
| 102 | 71 | 49 | 23 |
| 102 | 80 | 54 | 24 |
| 85 | 119 | 46 | 35 |
| 88 | 66 | 49 | 30 |
| 90 | 84 | 50 | 30 |
| 84 | 94 | 46 | 33 |
| 83 | 73 | 47 | 32 |
| 87 | 59 | 47 | 31 |
| 102 | 79 | 52 | 24 |
| 80 | 116 | 44 | 36 |
| 80 | 103 | 48 | 33 |
| 96 | 76 | 52 | 27 |
| 95 | 89 | 52 | 27 |
| 81 | 66 | 45 | 34 |
Провести предварительный анализ (описательную статистику) исследуемых компонентов многомерной случайной величины
Для всех пар случайных величин построить диаграммы рассеивания (корреляционные поля).
Рассчитать матрицу выборочных парных коэффициентов корреляции. Сделать выводы о степени тесноты и тенденции связи между парами компонентов исследуемого многомерного признака в терминах решаемой прикладной задачи.
Проверить гипотезу об отсутствии корреляционной связи между двумя компонентами случайной величины (X,Z).
Построить доверительные интервалы для двух парных коэффициентов корреляции при р=0.95 (X,Z;Y,Z).
Исключив из рассмотрения случайную величину, не зависящую от других, для оставшихся случайных величин рассчитать матрицу частных коэффициентов корреляции.
Рассчитать парные ранговые коэффициенты корреляции Спирмена и Кендалла для двух компонентов многомерной случайной величины (U,Y).
Рассчитать корреляционные отношения между случайными величинами, для которых можно предположить наличие нелинейной связи.
Рассчитать коэффициент конкордации для трех случайных величин, между которыми на основе проведенного анализа можно предположить наличие статистической связи.
Проверить гипотезу о статистической значимости исследуемой множественной связи.
В терминах решаемой прикладной задачи дать содержательную интерпретацию результатов для каждого из пунктов.
РЕШЕНИЕ
1. Построим диаграммы рассеивания
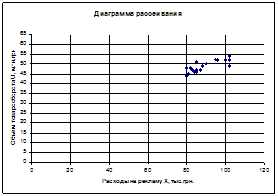
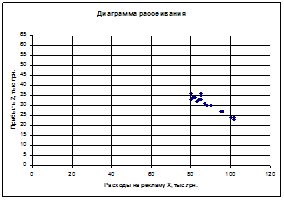
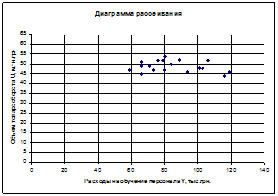
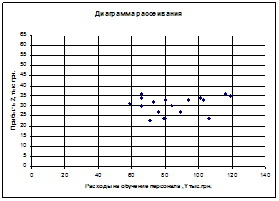
2. Рассчитаем матрицу выборочных парных коэффициентов корреляции при помощи пакета анализа программы Excel:
| Δ U | Δ X | Δ Y | |
| Δ U | 1 | ||
| Δ X | 0,80766 | 1 | |
| Δ Y | -0,3689 | -0,19614 | 1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, т.е. объем товарооборота предприятия торговли имеет сильную прямую связь с расходами предприятия на рекламу и продвижение товаров на рынок (0,4≤0,81≤1) и слабую обратную связь с расходами на обучение и повышение квалификации персонала (0,37≤0,4). Мультиколлинеарность отсутствует, т.к. коэффициент парной корреляции равен -0,196, что не превышает значения 0,7-0,8.
| Δ Z | Δ X | Δ Y | |
| Δ Z | 1 | ||
| Δ X | -0,95998 | 1 | |
| Δ Y | 0,215933 | -0,19614 | 1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, т.е. прибыль предприятия торговли имеет сильную обратную связь с расходами предприятия на рекламу и продвижение товаров на рынок (0,4≤0,96≤1) и слабую прямую связь с расходами на обучение и повышение квалификации персонала (0,22≤0,4). Мультиколлинеарность отсутствует, т.к. коэффициент парной корреляции равен -0,196, что не превышает значения 0,7-0,8.
3. Проверить гипотезу об отсутствии корреляционной связи между двумя компонентами случайной величины (X,Z):
В предыдущем пункте проверка гипотезы об отсутствии корреляционной связи между расходами предприятия на рекламу и продвижение товаров на рынок и прибылью предприятия была опровергнута, т.к. проверка коэффициентов парной корреляции показывает, что зависимая переменная, т.е. прибыль предприятия торговли имеет сильную обратную связь с расходами предприятия на рекламу и продвижение товаров на рынок (0,4≤0,96≤1).
Похожие работы
... метод – 10-4-10-6 Микроскопия – 10-4-10-7 Метод фильтрации – 10-5-10-7 Центрифугирование – 10-6-10-8 Ультрацентрифугирование – 10-7-10-9 Ультрамикроскопия – 10-7-10-9 Нефелометрия – 10-7-10-9 Электронная микроскопия – 10-7-10-9 Метод диффузии – 10-7-10-10 Дисперсионный анализ широко используют в различных областях науки и промышленного производства для оценки дисперсности систем ( ...
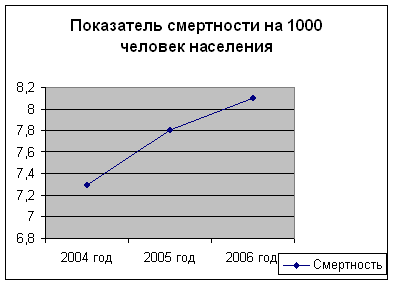
... отклика является смертность населения в конкретной возрастной группе, а факторами, влияющими на ее изменение, являются классы заболеваний. 2.2. Дисперсионный анализ Методом дисперсионного анализа, выясним, оказывает ли влияние различные заболевания на показатель смертности населения. То есть, проверим, выполняется ли гипотеза о равенстве математических ожиданий (Н0: М(Х1) = М(Х2) = … = ...
... группы, установление связи и ее направление. Индексный метод является гибким аналитическим инструментом и может применяться в анализе показателе производственной, финансовой, инвестиционной и других видах деятельности предприятия (фирмы). Корреляционный и регрессионный анализ являются довольно сложной операцией. Исходными предпосылками для их проведения являются: случайный характер факторов, ...
... . Это позволяет определить, какие из основных задач финансового анализа и в какой степени, а также в какой очередности следует решать при выполнении комплексного анализа. §3. Информационная основа финансового анализа, его пользователи Информационными источниками для расчета показателей и проведенияанализа служат годовая, квартальная и месячная бухгалтерская отчетность, а также данные ...
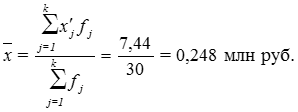
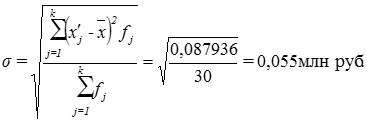
0 комментариев